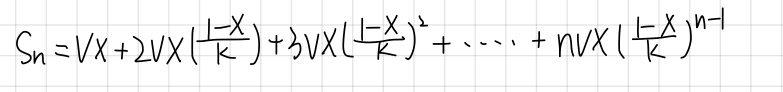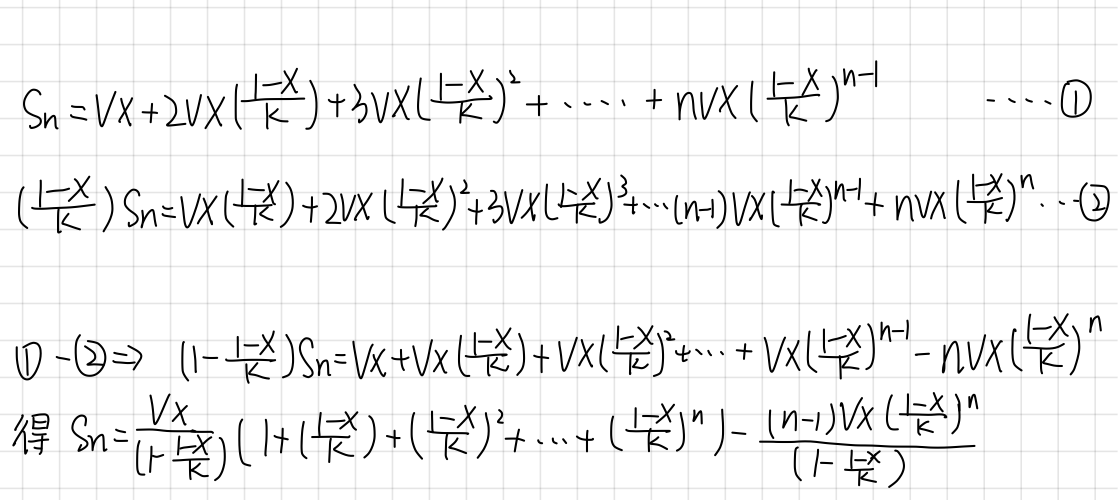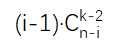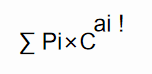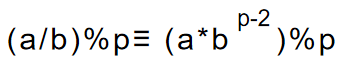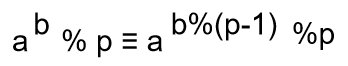UPC Contest RankList – 2019年第二阶段我要变强个人训练赛第十六场
E: 飞碟解除器
•题目描述
wjyyy在玩跑跑卡丁车的时候,获得了一个飞碟解除器,这样他就可以免受飞碟的减速干扰了。
飞碟解除器每秒末都会攻击一次飞碟,但每次只有p/q的概率成功攻击飞碟。当飞碟被成功攻击时,减速状态解除。
如果攻击失败,飞碟会使wjyyy的平均速度变为前一秒的1/k倍。
wjyyy一开始以v m/s的速度行驶,问在减速状态解除时,他期望的行驶距离对998244353取模的结果。输入
输入共一行,共4个非负整数k,p,q,v。其中gcd(p,q)=1。输出
输出共一行,表示wjyyy的期望行走距离对998244353取模的结果。样例输入
2 2 3 9样例输出
119789331提示
对于100%的数据,gcd(p,q)=1,1≤k≤998244352,1≤p≤q≤998244352,0≤v≤998244352
提示wjyyy在第一秒走过的距离是v m,如果他此时没有攻击成功,则在第二秒后走过的距离是2×v/k m。
以此类推。
•思路
假设在每秒末飞碟解除
总距离相加得
显而易见(大雾)是一个差比数列前n项和
然后我们就开始高三数学每套试卷都有的错位相减
由于n是趋近于正无穷的所有最后一项
的极限为0
所以Sn的极限与等比数列前n项和有关
所以Sn极限为
•代码
F: gu集合
•题目描述
Dew有一个长为n的集合S。有一天,他想选k个不同的元素出来做游戏。
但是Dew只有两只手,所以他只能先选出k个元素,然后拿出这k个元素中最小的两个。
事实上,Dew更喜欢这k个元素中第二小的那个,因此他会记一个集合T的第二小值为g(T)。此时Dew可以获得c^g(T)!的得分,其中c是一个常数,!表示阶乘。
现在你需要求出Dew从集合S中选出k个元素后,他的期望得分对998244353取模的结果。输入
输入共两行。
第一行三个正整数n,k,c,分别表示集合S的大小,Dew要选的元素个数,和常数c。
第二行n个互不相同的正整数ai,表示集合S中的元素。保证。
输出
输出一行一个非负整数,表示 Dew 的期望得分对998244353取模的结果。样例输入
5 3 2
1 2 3 4 5样例输出
803628674
•思路
有n个数a1,a2,a3,a4,....(升序排列),从中选出k个,
总的情况数是C(n,k)种,
其中a2是第二小数的有C(n-2,k-2)个,a2是第二小,肯定得选a1,a2,再从剩下的(n-2)个里选出(k-2)个
其中a3是第二小数的有2*C(n-3,k-2)个,a3是第二小,肯定得选且只能选a1,a2中的一个即两种情况,再从剩下的(n-3)个里选出(k-2)个
其中a4是第二小数的有3*C(n-4,k-2)个,a4是第二小,肯定得选且只能选a1,a2,a3中的一个即三种情况,再从剩下的(n-4)个里选出(k-2)个
...
得到选每个数的情况是
所以被选择的期望
然后再乘以阶乘,最终结果为
•细节处理
除法取模:
指数取模:
•代码
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define mod 998244353
const int maxn=5e5+;
const int maxnn=1e7+;
ll fac[maxn];
ll facc[maxnn];
ll a[maxn]; ll quickMod(ll x,ll y)
{
ll res=;
x=x%mod;
while(y)
{
if(y&)
res=res*x%mod;
x=x*x%mod;
y>>=;
}
return res%mod;
} ll getfac()
{
fac[]=;
for(int i=;i<5e5+;i++)
fac[i]=fac[i-]*i%mod;
} ll getfacc()
{
facc[]=;
for(int i=;i<1e7+;i++)
facc[i]=facc[i-]*i%(mod-);
} int main()
{
int n,k,c;
cin>>n>>k>>c;
getfac();
getfacc();
for(int i=;i<=n;i++)
cin>>a[i];
ll ans=;
for(int i=;i<=n;i++)
{
if(n-i<k-)//防止组合数越界
break;
ans=(ans%mod+(i-)*fac[n-i]%mod*fac[n-k]%mod*fac[k]%mod*quickMod(fac[n-i-k+]*fac[k-]%mod*fac[n]%mod,mod-)%mod*quickMod(c,facc[a[i]])%mod)%mod;;
}
cout<<ans<<endl;
}
UPC Contest RankList – 2019年第二阶段我要变强个人训练赛第十六场的更多相关文章
- UPC Contest RankList – 2019年第二阶段我要变强个人训练赛第十四场
A.JOIOJI •传送门 [1]:BZOJ [2]:洛谷 •思路 在一个区间(L,R]内,JOI的个数是相等的,也就是R[J]-L[J]=R[O]-L[O]=R[I]-L[I], 利用前缀和的思想, ...
- UPC Contest RankList – 2019年第二阶段我要变强个人训练赛第十五场
传送门 A: Colorful Subsequence •题意 给一个长为n的小写字母序列,从中选出字母组成子序列 问最多能组成多少种每个字母都不相同的子序列 (不同位置的相同字母也算是不同的一种) ...
- UPC 2019年第二阶段我要变强个人训练赛第十六场
传送门: [1]:UPC比赛场 [2]:UPC补题场 F.gu集合(数论) •题目描述 题目描述: Dew有一个长为n的集合S. 有一天,他想选k个不同的元素出来做游戏. 但是Dew只有两只手,所以他 ...
- UPC 2019年第二阶段我要变强个人训练赛第六场
传送门 A.上学路线 题目描述 小D从家到学校的道路结构是这样的:由n条东西走向和m条南北走向的道路构成了一个n*m的网格,每条道路都是单向通行的(只能从北向南,从西向东走). 已知小D的家在网格的左 ...
- 2019年第二阶段我要变强个人训练赛第八场 B.序列(seq)
传送门 B.序列(seq) •题目描述 给出一个长度为n的序列a,每次对序列进行一下的某一个操作. •输入 第一行两个整数n,q表示序列长度和操作个数. 接下来一行n个数,表示序列a. 接下来q行表示 ...
- 备战省赛组队训练赛第十六场(UPC)
传送门 题解: by 烟台大学 (提取码:8972)
- UPC个人训练赛第十五场(AtCoder Grand Contest 031)
传送门: [1]:AtCoder [2]:UPC比赛场 [3]:UPC补题场 参考资料 [1]:https://www.cnblogs.com/QLU-ACM/p/11191644.html B.Re ...
- 备战省赛组队训练赛第十四场(UPC)
codeforces:传送门 upc:传送门 外来题解: [1]:https://blog.csdn.net/ccsu_cat/article/details/86707446 [2]:https:/ ...
- 备战省赛组队训练赛第十八场(UPC)
传送门 题解:by 青岛大学 A:https://blog.csdn.net/birdmanqin/article/details/89789424 B:https://blog.csdn.net/b ...
随机推荐
- flask(三)
1.cbv的用法 from flask import Flask,views app = Flask(__name__) class Login(views.MethodView ): def get ...
- 快速删除mysql表中的数据
一.清空全部数据,不写日志,不可恢复,速度很快 truncate table 表名; 二.清空全部数据,写日志,可恢复,速度很慢 delete from 表名;
- Hive的一些学习内容
Hive相关 什么是metastore? metadata是元数据,包含数据库.表.字段.分区等信息.作用:客户端连接MetaStore服务,metastore再去连接MySQL数据库存储元数据,有了 ...
- 给 Windows 的终端配置代理
初衷 由于项目开发使用go,所以经常要用到go get,但是吧,terminal下根本没办法下载啊,经常下载三个小时包,写代码一个小时 迫于无奈,只好找个方式可以在terminal下使用ss cmd下 ...
- Python 爬虫从入门到进阶之路(十一)
之前的文章我们介绍了一下 Xpath 模块,接下来我们就利用 Xpath 模块爬取<糗事百科>的糗事. 之前我们已经利用 re 模块爬取过一次糗百,我们只需要在其基础上做一些修改就可以了, ...
- 如何把设计稿中px值转化为想要的rem值
首先我们需要的是把尺寸转化为rem值 假如 设计稿中的是 200px*200px的图片 移动端的设计图尺寸一般是640*750; 第一步. 把图片分为若干份(好算即可),每一份的大小就是rem的单位 ...
- 搭建本地pip源
搭建本地的pip源 开发环境部署机器的时候, 每次从网上下载pip包会很慢, 将需要的包和相关依赖下载到本地, 搭建一个本地源服务器. 基本都是安装多个包, 推荐使用文件的方式, 文件内容格式, 可以 ...
- 18 | 眼前一亮:带你玩转GUI自动化的测试报告
- KVM web管理工具——WebVirtMgr
系统环境: [root@kvm-admin ~]# cat /etc/redhat-release CentOS Linux release (Core) 关闭防火墙.selinux [root@kv ...
- 源码阅读 - java.util.concurrent (三)ConcurrentHashMap
在java.util.concurrent包中提供了一个线程安全版本的Map类型数据结构:ConcurrentMap.本篇文章主要关注ConcurrentMap接口以及它的Hash版本的实现Concu ...