算法修养--A*寻路算法

A*寻路算法

广度优先算法

广度优先算法搜索以广度做未优先级进行搜索。

从起点开始，首先遍历起点周围邻近的点，然后再遍历已经遍历过的点邻近的点，逐步的向外扩散，直到找到终点。

这种算法就像洪水（Flood fill）一样向外扩张。直至洪水将整张地图都漫延。在访问节点时候，每个点需要记录到达该点的前一个点的位置（父节点），访问到终点时候，便可以从终点沿着父节点一路走回到起点，从而找出路径。（注意：这也是A*算法的一部分）

这种洪水蔓延式寻找路径的方式较为野蛮粗暴，仅仅依据广度来找路径，难以找到最短的路径。

Dijkstra算法

在实际寻路场景中，要考虑“移动成本”。不同的路径有不同的成本，例如，穿过平原或沙漠可能需要 1 个移动点，但穿过森林或丘陵可能需要 5 个移动点。玩家在水中行走的成本是在草地上行走的 10 倍。为此我们需要Dijkstra算法。

在Dijkstra算法中，需要计算每一个节点距离起点移动的总移动代价，同时，还需要一个优先队列结构，对于所有待遍历的节点，放入优先队列中，优先队列会按照代价进行排序。（这也是在下面要介绍的A*算法实现案例中待优化的点！）

在算法运行过程中，每次都从优先队列中选出移动成本最小的作为下一个要遍历检查的节点，直到访问到达终点为止。

两种算法的对比：

考虑这样一种场景，在一些情况下，图形中相邻节点之间的移动代价并不相等。例如，游戏中的一幅图，既有平地也有山脉，那么游戏中的角色在平地和山脉中移动的速度通常是不相等的。

在Dijkstra算法中，需要计算每一个节点距离起点的总移动代价。同时，还需要一个优先队列结构。对于所有待遍历的节点，放入优先队列中会按照代价进行排序。

在算法运行的过程中，每次都从优先队列中选出代价最小的作为下一个遍历的节点。直到到达终点为止。

下面对比了不考虑节点移动代价差异的广度优先搜索与考虑移动代价的Dijkstra算法的运算结果：

广度优先算法： Dijkstra算法：

当然，如果不考虑移动代价的因素，在同一个网格图中Dijkstra算法将和广度优先算法一样。

启发式搜索？

通过广度优先搜索和 Dijkstra 算法，边界向各个方向扩展。如果试图找到通往所有位置或许多位置的路径，这是一个合理的选择。

如果仅仅是找到到达一个位置的路径，我们应当控制洪水的流向，时期朝向目标位置流动。而控制方向的条件判断便可以通过启发式搜索来完成。

而所谓启发式搜索函数便是用来计算当前点到达目标点的距离（步数），预测到达目标点的距离。

启发函数来计算到目标点距离方式有多种选择：

• 曼哈顿距离

  如果图形中只允许朝上下左右四个方向移动，则启发函数可以使用曼哈顿距离，它的计算方法如下图所示：

  

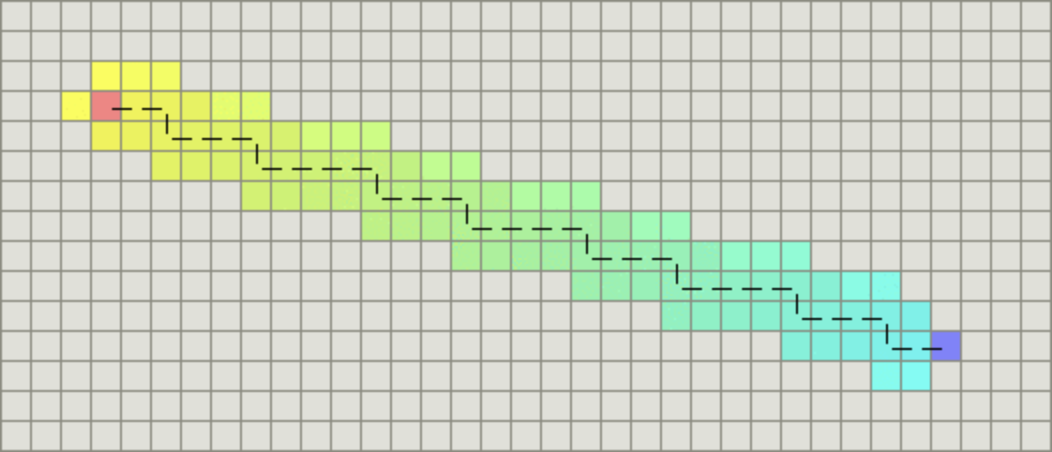
  曼哈顿距离=abs(node.x-target.x)+abs(node.y-target.y)

• 对角移动

  如果图形中允许斜着朝邻近的节点移动，则启发函数可以使用对角距离。

  

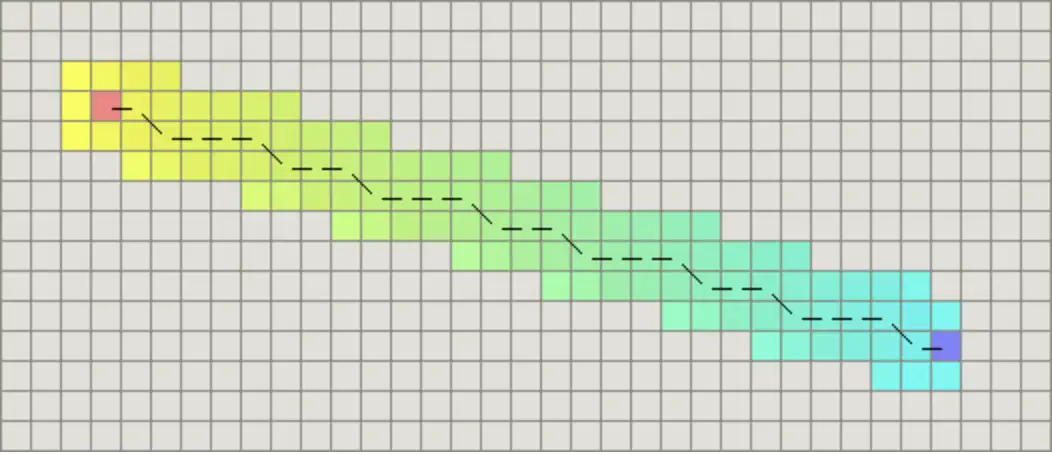
• 欧几里得距离

  如果图形中允许朝任意方向移动，则可以使用欧几里得距离。

  欧几里得距离²=（node.x-target.x）²+(node.y-target.y)²

采用启发函数控制广度优先搜索的方式为（贪婪）最佳优先搜索。

最佳优先搜索（Best First）

最佳优先搜索的原理也简单，与Dijkstra算法类似（广度优先+移动成本），也使用一个优先队列存储启发函数值（该点与目标点的距离），每次选取与目标点最近的点（邻居）来访问，直至访问到终点。

可以理解算法是广度优先算法+选择最小目标点距离参数的结果。

同样，由于没有考虑移动成本，在移动成本不同的地图中也不能考虑到森林、沼泽等移动速度不同的场景造成的移动成本的增加。不能保证找到的路径是最短的路径。

那就结合在一起呗！

A*算法=广度优先算法+考虑“移动成本”+考虑“与目标点的距离”；

既可以保证聪明地选择好走的路线避开难走的路线或者障碍物，也可以集中管控搜索方向向着目标点中的位置搜寻。

下面是对三个算法的详细对比：

A*算法集合了前两个算法的优势，可以保证在两点之间找到最佳的路线。

A*寻路算法

基本原理：

A*算法使用如下所示的函数来计算每个节点的优先级：

\[f(n)=g(n)+h(n)
\]

f(n)是节点n的综合优先级。

g(n)表示节点n距离起点的代价（距离或步数），即：从起点出发到达当前点所走的步数；

h(n)则表示节点n距离终点（目标点）的预估代价，即：从当前点达到终点需要走的步数，这是A*算法的启发函数，相当于提前预测要走到目标点还需要的步数。由于是预测，按照最短的路径（步数）来表示，所以实际上到达终点的路程要等于或大于预测的数值。

寻路算法的启发函数控制：（理解两个参数对搜寻的影响）

• 在极端情况下，当启发函数h(n)始终为0，则将由g(n)决定节点的优先级，此时算法就退化成了Dijkstra算法。
• 如果h(n)始终小于等于节点n到终点的代价，则A*算法保证一定能够找到最短路径。但是当h(n)的值越小，算法将遍历越多的节点，也就导致算法越慢。
• 如果h(n)完全等于节点n到终点的代价，则A*算法将找到最佳路径，并且速度很快。可惜的是，并非所有场景下都能做到这一点。因为在没有达到终点之前，我们很难确切算出距离终点还有多远。
• 如果h(n)的值比节点n到终点的代价要大，则A*算法不能保证找到最短路径，不过此时会很快。
• 在另外一个极端情况下，如果h()n相较于g(n)大很多，则此时只有h(n)产生效果，这也就变成了最佳优先搜索。

在寻路过程中，每次依据周边节点的f(n)数值来选择,每次选择最小的f(n)；

有障碍物的情况下的寻路（黑色方块为障碍物）

代码实现：

//节点类
public class NodeBase{
    public NodeBase Connection{get;private set;}//存储自己的相连接路径中的节点
    public float G{get;private set;}
    public float H{get;private set;}
    public float F=>G+H;

    public void SetConnetion(NodeBase nodeBase)=>Connection=nodeBase;
    public void SetG(float g)=>G=g;
    public void SetH(float h)=>H=h;
}

//核心算法
public static class Pathfinding {
    /// <summary>
    /// A*算法核心
    /// </summary>
    /// <param name="startNode">开始点</param>
    /// <param name="targetNode">目标点</param>
    /// <returns>最短路径</returns>
    /// <exception cref="Exception"></exception>
    public static List<NodeBase> FindPath(NodeBase startNode, NodeBase targetNode) {
        var toSearch = new List<NodeBase>() { startNode };//要处理搜寻的节点（未访问过）
        var processed = new List<NodeBase>();//存储访问过的节点

        while (toSearch.Any()) {//判断是否有要搜寻的元素节点
            //fixit 待优化的点 可以使用一个堆排序思想
            var current = toSearch[0];
            foreach (var t in toSearch)
                if (t.F < current.F || t.F == current.F && t.H < current.H) current = t;

            processed.Add(current);
            toSearch.Remove(current);//搜寻过后就移除

            current.SetColor(ClosedColor);

            //终点检查
            if (current == targetNode) {
                var currentPathTile = targetNode;
                var path = new List<NodeBase>();//保存路径
                var count = 100;
                //从终点到出发点的节点路径寻找
                while (currentPathTile != startNode) {
                    path.Add(currentPathTile);
                    currentPathTile = currentPathTile.Connection;
                    count--;//这里根据地图的大小设置一个路径长度极限（可以忽略）
                    if (count < 0) throw new Exception();
                    Debug.Log("sdfsdf");
                }
                foreach (var tile in path) tile.SetColor(PathColor);
                startNode.SetColor(PathColor);
                Debug.Log(path.Count);
                return path;//返回路径
            }
            //关心一下自己的邻居--可以到达的邻居，并且还未访问过的（非障碍物）
            foreach (var neighbor in current.Neighbors.Where(t => t.Walkable && !processed.Contains(t))) {
                var inSearch = toSearch.Contains(neighbor);//获取对邻居的访问状况
                var costToNeighbor = current.G + current.GetDistance(neighbor);
                //更新一下邻居的G值
                //对于已经访问过的邻居 如果从另一个方向过来想再次访问，那么G值应当比之前访问的要小（只能是最近路程访问）
                if (!inSearch || costToNeighbor < neighbor.G) {
                    neighbor.SetG(costToNeighbor);
                    neighbor.SetConnection(current);//记录与之连接的节点（算作路径中）
                    //如果是第一次访问 还需要进行H值的计算
                    if (!inSearch) {
                        neighbor.SetH(neighbor.GetDistance(targetNode));//计算启发函数值
                        toSearch.Add(neighbor);//将邻居添加到要访问的列表中
                    }
                }
            }
        }
        return null;
    }
}

---

参考文章：https://www.redblobgames.com/pathfinding/a-star/introduction.html

参考视频：https://www.youtube.com/watch?v=i0x5fj4PqP4

参考项目：https://github.com/zhm-real/PathPlanning