poj 1410 线段相交判断

http://poj.org/problem?id=1410

Intersection

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 11329		Accepted: 2978

Description

You are to write a program that has to decide whether a given line segment intersects a given rectangle.

An example: 
line: start point: (4,9) 
end point: (11,2) 
rectangle: left-top: (1,5) 
right-bottom: (7,1)

 
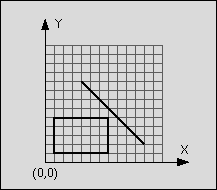
Figure 1: Line segment does not intersect rectangle

The line is said to intersect the rectangle if the line and the rectangle have at least one point in common. The rectangle consists of four straight lines and the area in between. Although all input values are integer numbers, valid intersection points do not have to lay on the integer grid.

Input

The input consists of n test cases. The first line of the input file contains the number n. Each following line contains one test case of the format: 
xstart ystart xend yend xleft ytop xright ybottom

where (xstart, ystart) is the start and (xend, yend) the end point of the line and (xleft, ytop) the top left and (xright, ybottom) the bottom right corner of the rectangle. The eight numbers are separated by a blank. The terms top left and bottom right do not imply any ordering of coordinates.

Output

For each test case in the input file, the output file should contain a line consisting either of the letter "T" if the line segment intersects the rectangle or the letter "F" if the line segment does not intersect the rectangle.

Sample Input

1
4 9 11 2 1 5 7 1

Sample Output

F

Source

Southwestern European Regional Contest 1995

 

‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’

---------------------------------------------------------------------------------------------------------------

题目有点坑，没有说明输入的不一定是左上，以及右下，可能会是左下，以及右上

并且，包含在矩形里也算相交，这题看题解不是好想法啊，自己想出来比较好

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <iostream>
#include <algorithm>
#include <math.h>

using namespace std;
typedef struct point
{
    int x,y;
}point;

typedef struct line
{
    point st,ed;
}line;

int crossProduct(point a,point b,point c)
{
    return (c.x-a.x)*(b.y-a.y)-(c.y-a.y)*(b.x-a.x);
}

bool onSegment(point a,point b,point c)
{
    int maxx=max(a.x,b.x);
    int maxy=max(a.y,b.y);
    int minx=min(a.x,b.x);
    int miny=min(a.y,b.y);
    if(crossProduct(a,b,c)==&&(c.x<=maxx)&&(c.x>=minx)&&(c.y<=maxy)&&(c.y>=miny))
    {
        return true;
    }
    return false;
}

bool segIntersect(point p1,point p2,point p3,point p4)
{
    int d1=crossProduct(p3,p4,p1);
    int d2=crossProduct(p3,p4,p2);
    int d3=crossProduct(p1,p2,p3);
    int d4=crossProduct(p1,p2,p4);
    if(d1*d2< && d3*d4<)
        return true;
    if(d1== && onSegment(p3,p4,p1))
        return true;
    if(d2== && onSegment(p3,p4,p2))
        return true;
    if(d3== && onSegment(p1,p2,p3))
        return true;
    if(d4== && onSegment(p1,p2,p4))
        return true;
    return false;
}

point p[];
line li[];
int num[];

int main()
{
    int n,m,i,j;
    line tmp;
    int xleft,ytop,xright,ybottom;
    scanf("%d",&n);
    while(n--)
    {
        scanf("%d%d%d%d%d%d%d%d",&tmp.st.x,&tmp.st.y,&tmp.ed.x,&tmp.ed.y
              ,&xleft,&ytop,&xright,&ybottom);
        li[].st.x=xleft;
        li[].st.y=ytop;
        li[].ed.x=xleft;
        li[].ed.y=ybottom;

        li[].st.x=xleft;
        li[].st.y=ybottom;
        li[].ed.x=xright;
        li[].ed.y=ybottom;

        li[].st.x=xright;
        li[].st.y=ybottom;
        li[].ed.x=xright;
        li[].ed.y=ytop;

        li[].st.x=xright;
        li[].st.y=ytop;
        li[].ed.x=xleft;
        li[].ed.y=ytop;

        bool flag=true;
        for(i=;i<;i++)
        {
            if(segIntersect(tmp.st,tmp.ed,li[i].st,li[i].ed))
            {
                flag=false;
                break;
            }
        }

        int maxx=max(xleft,xright);
        int maxy=max(ytop,ybottom);
        int minx=min(xleft,xright);
        int miny=min(ytop,ybottom);
        if(tmp.st.x<=maxx&&tmp.st.x>=minx&&tmp.st.y>=miny&&tmp.st.y<=maxy
           ||tmp.ed.x<=maxx&&tmp.ed.x>=minx&&tmp.ed.y>=miny&&tmp.ed.y<=maxy)
            flag=false;

        if(flag)
            printf("F\n");
        else printf("T\n");
    }
    return ;
}