浅谈算法——KMP

KMP是啥？KMP当然是KMPlayer的简称啦

KMP算法是用来解决字符串匹配的一种算法，由D.E.Knuth、J.H.Morris和V.R.Pratt同时发现，然后它可以用来干啥呢？我们上个例题：

给定两个字符串\(S,T\)，问\(T\)在\(S\)中出现了多少次，出现的起始位置不同即为不同

\(O(n^2)\)暴力！(我当然知道你会)

\(|S|,|T|\leqslant 10^5\)，怎么做？

所以这时我们就需要引入KMP算法，它能在最坏\(O(n)\)的复杂度下解决子串匹配的问题

首先我们考虑一下\(O(n^2)\)的冗余在哪里？举个栗子吧，我令S='aaaaaaaaac',T='aaaac'，然后跑一遍\(O(n^2)\)，你会发现每次\(S_{i+5}\)与\(T_5\)失配后，它会从\(S_{i+1}\)从头开始匹配，但是，其实没必要重新开始对吧？因此你发现这个\(O(n^2)\)的算法做了非常多没有意义的匹配，导致时间复杂度急剧增加，然后就TLE了

发现问题自然需要解决，如何解决？KMP算法就基于这个冗余提出了优化方案，它建立了一个对于任意字符串\(S\)而言的Next(C++11中next是关键字，所以我使用大写，并在之后简称为\(N\)数组)数组，\(N_i\)表示\([S_1...S_i]\)中前缀后缀相等的长度，也就是有\([S_1...S_{N_i}]=[S_{i-N_i+1}..S_i]\)，举个栗子，若字符串S='abcabc'，则它的\(N\)数组为\(\{0,0,0,1,2,3\}\)(\(N_1=0\)是定义的)

有了\(N\)数组后有何用？既然是为了解决冗余的，那我们就来看看它如何解决这个冗余。我们依然采用之前的栗子，首先对于\(T\)串求出其\(N\)数组：\(\{0,1,2,3,0\}\)，然后我们进行匹配，然后遇到\(S_5\)与\(T_5\)失配，然后怎么处理？

当然把它俩从头开始啊(\(n^2\)了啊喂，你\(N\)白求了)；你发现\(T_4\rightarrow T_5\)过程中与\(S_4\rightarrow S_5\)失配了，然后想想\(N\)数组的性质，可能存在\(T_{N_4}\rightarrow T_{N_4+1}\)能匹配啊，然后你就只需要把枚举\(T\)的指针疯狂跳\(N\)数组，直到能匹配为止

然后我们画个图来理解一下

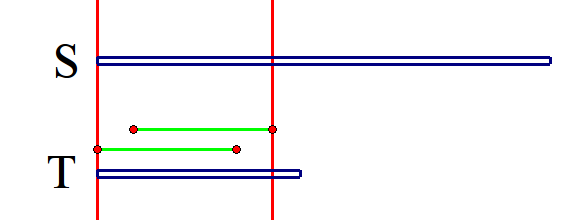
这里红色平行线之间的完全相同的部分，之后就是失配的字符，绿色的便是后缀和前缀相同的部分

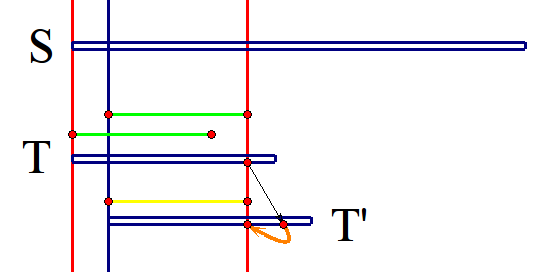
然后我们就将T往后挪一点点，黄色部分和绿色部分相同，然后黑色箭头则说明T中的位置在T'中对应的位置，棕色箭头即为跳\(N\)数组的过程

然后我们贴个代码

for (int i=1,j=0;i<=Lens;i++){
	while (j&&s[i]!=t[j+1])	j=Next[j];
	if (s[i]==t[j+1])	j++;
	if (j==Lent)	j=Next[j],Ans++;//就算匹配了也要跳一次匹配其他的，因为是统计出现次数
}

然后这题就做完了对吧？不对，我还没有讲\(N\)数组的构造方法……其实构造方法和匹配差不多，贴个代码，读者们可以自己看下

for (int i=2,j=0;i<=Lent;i++){
	while (j&&t[i]!=t[j+1])	j=Next[j];
	if (t[i]==t[j+1])	j++;
	Next[i]=j;
}

然后我们来考虑一下时间复杂度，显然是\(O(n)\)的，做道例题吧

洛谷P3375 【模板】KMP字符串匹配

求\(T\)在\(S\)中的出现位置，并且输出\(T\)的Next数组

直接套用板子就好

#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define inf 0x7f7f7f7f
using namespace std;
typedef long long ll;
typedef unsigned int ui;
typedef unsigned long long ull;
inline int read(){
	int x=0,f=1;char ch=getchar();
	for (;ch<'0'||ch>'9';ch=getchar())	if (ch=='-')    f=-1;
	for (;ch>='0'&&ch<='9';ch=getchar())	x=(x<<1)+(x<<3)+ch-'0';
	return x*f;
}
inline void print(int x){
	if (x>=10)     print(x/10);
	putchar(x%10+'0');
}
const int N=1e6;
char t[N+10],s[N+10];
int Next[N+10];
int Lens,Lent,ans;
void get(){
	for (int i=2,j=0;i<=Lent;i++){
		while (j&&t[i]!=t[j+1])	j=Next[j];
		if (t[i]==t[j+1])	j++;
		Next[i]=j;
	}
}
void work(){
	get();
	for (int i=1,j=0;i<=Lens;i++){
		while (j&&s[i]!=t[j+1])	j=Next[j];
		if (s[i]==t[j+1])	j++;
		if (j==Lent)	j=Next[j],printf("%d\n",i-Lent+1);
	}
}
int main(){
	scanf("%s",s+1);
	scanf("%s",t+1);
	Lens=strlen(s+1),Lent=strlen(t+1),ans=0;
	work();
	for (int i=1;i<=Lent;i++)	i!=Lent?printf("%d ",Next[i]):printf("%d\n",Next[i]);
	return 0;
}