HGOI 20181030晚 题解

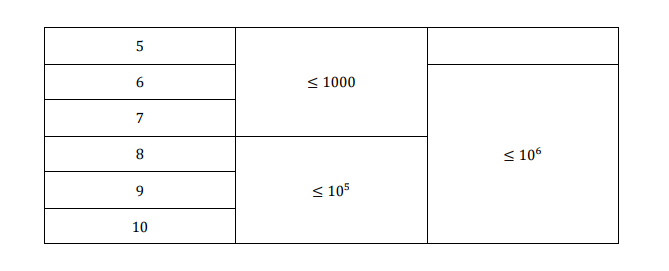
Problem:给出全班人的个数总分和小明的分数(满分100分)，求小明最低排名和最高排名

sol：假设小明的排名为k，总分为sum，小明的分数是r，

贪心求解，

最坏情况下，小明前面的比小明高一分(r+1)分，那么给后面的人的分数是sum-(k-1)*(r+1)-r

最优情况下，小明前面的人都是满分(100)分，那么给后面人的分数是sum-(k-1)*100-r

所以对于后面人分数的取值范围是A=[sum-(k-1)*100-r，sum-(k-1)*(r+1)-r]

而对于一个很显然的结论由于小明是第k名所以在他后面(含一样的分数)有n-k人，他们的分数的取值范围是B=[0,(n-k)*r]

如果说A和B有交集的话该问题有解，可以求出连续的一段范围求最小的l，最大的r

判断交集快速的方法是

1. 判包含关系。

2.判某条线段的左右断点是不是在另外一条线段内。

# include<bits/stdc++.h>
using namespace std;
bool check(int l1,int r1,int l2,int r2)
{
    if (l1>r1) swap(l1,r1);
    if (l2>r2) swap(l2,r2);
    if (l1>=l2&&r2>=r1) return ;
    if (l2>=l1&&r1>=r2) return ;
    if (l2>=l1&&l2<=r1) return ;
    if (r2>=l1&&r2<=r1) return ;
    return ;
}
int main()
{
    int N,A,S;
    scanf("%d%d%d",&N,&A,&S);
    if (A==) { puts("1 1");return ; }
    int l=N,r=;
    for (int i=;i<=N;i++)
     if (check(S-(i-)*(A+)-A,S-(i-)*-A,,A*(N-i))) {
        l=min(l,i); r=max(r,i);
     }
    printf("%d %d\n",l,r);
    return ;
 }

sol：考虑问题平方和就是要大的数尽可能大，通过题目中所说的东西

• rec1=a or b
• rec2=a and b
• a=rec1 ,b=rec2

发现本质其实是把两个数的某个二进制位交换，所以最后就是每位有若干的1，让你分配到对应的位置，最大化平方和

就是尽可能放大的数，然后平方以后就是最大的。

# include <bits/stdc++.h>
# define int long long
using namespace std;
const int MAXN=;
int b[MAXN],n;
inline int read()
{
    int X=,w=; char c=;
    while (!(c>=''&&c<='')) w|=c=='-',c=getchar();
    while (c>=''&&c<='') X=(X<<)+(X<<)+(c^),c=getchar();
    return w?-X:X;
}
void getbit(int x)
{
    for (int i=;i<=;i++)
     if ((x>>i)&==) b[i]++;
}
signed main()
{
    n=read(); int x;
    for (int i=;i<=n;i++) x=read(),getbit(x);
    int num=;for (int i=;i<=;i++) num+=b[i];
    int ans=;
    while () {
        if (num==) break;
        int tmp=;
        for (int i=;i>=;i--)
         if (b[i]>) b[i]--,tmp+=(<<i),num--;
        ans+=tmp*tmp;
    }
    cout<<ans<<endl;
    return ;
}

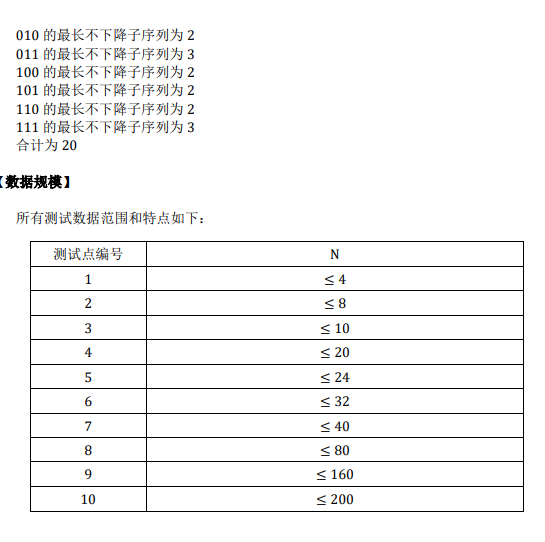
sol:一道DP题其实比较简单

一开始状态定义错了，导致最长不下降子序列弄错了(其实和前面0的个数有关系)

f[i][j][k]前i个，有j个0，LIS长度为k个的数的可能性

若第i+1位为0，那么f[i+1][j+1][k]+=f[i][j][k]

若第i+1位为1，那么f[i+1][j][max(k,j)]+=f[i][j][k]

为什么是max(k,j)呢？ 由于第i+1位为是1那么和前面有j个0构成一个最长上升子序列长度是j，

而此时加入一个1才到达长度为k，那么此时最长的长度可能并不会发生更新，可能还是前面都是0的子序列更优(一开始没有把0的个数作为一个状态！)

初始值f[0][0][0]=1

# include <bits/stdc++.h>
# define int long long
using namespace std;
const int MAXN=;
const int mo=1e9+;
int n;
int f[MAXN][MAXN][MAXN];
inline int read()
{
    int X=,w=; char c=;
    while (!(c>=''&&c<='')) w|=c=='-',c=getchar();
    while (c>=''&&c<='') X=(X<<)+(X<<)+(c^),c=getchar();
    return w?-X:X;
}
signed main()
{
    n=read();  memset(f,,sizeof(f));
    f[][][]=;
    //f[i][j][k]前i个，有j个0，长度为k个数
    for (int i=;i<=n;i++)
     for (int j=;j<=n;j++)
      for (int k=;k<=n;k++)
      {
        f[i+][j+][k]=(f[i+][j+][k]+f[i][j][k])%mo;
        f[i+][j][max(k,j)+]=(f[i+][j][max(k,j)+]+f[i][j][k])%mo;
      }
      int ans=;
      for (int j=;j<=n;j++)
       for (int k=;k<=n;k++)
        ans=(ans+(max(k,j)*f[n][j][k])%mo)%mo;
      cout<<ans<<endl;
    return ;
}