【题解】 bzoj1875: [SDOI2009]HH去散步 （动态规划+矩阵乘法）

bzoj1875，懒得复制，戳我戳我

Solution:

• 看到这道题，看的出是个dp，每个点\(t\)时刻到达的方案数等于\(t-1\)到连过来的点方案数之和
• 但又因为题目有要求不能走一样的边回去不是说不能回到之前那个点，而是不能走一样的边
• 又因为\(t\)很大，每次我们的都是做的重复的操作，我们就可以想到矩阵快速幂
• 为了保证不走重边回去，我们就可以用一个骚操作，把边化作点，然后双向边可以看做两条单向边，然后把每条单向边看做节点，连向所（这条边连向的节点）连出去的边。但是不连这条边的反向边，这样就可以保证不走一样的路回去了（超级机智）
  
  
  
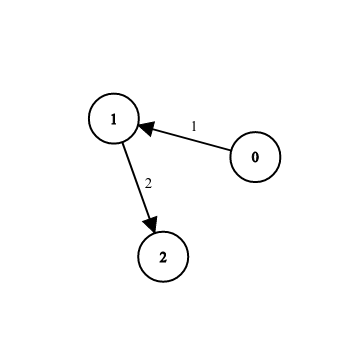
  如上图的\(1\)号边连向\(2\)号边，我们就可以把这个存在矩阵里面了
• 然后来一遍矩阵快速幂就好了，注意是\(t-1\)次，因为最后一次没走到，是到边上，没有回到\(B\)点
• 初始矩阵是把\(A\)点所有连出去的边\(+1\)，然后把初始矩阵乘以快速幂后的矩阵，\(ans\)就是最后得到矩阵中所有连向\(B\)边上存的值和
• 丢一个我觉得讲的很清楚的博客

Attention:

• 会有重复边，所以矩阵里面是\(+1\)，不是直接赋值为\(1\)
• 不能走一样的路回去，可以走另一条路回到先前的点

Code:

//It is coded by Ning_Mew on 5.10
#include<bits/stdc++.h>
#define IL inline
using namespace std;

const int maxn=125,MOD=45989;

int n,m,t,A,B,out=0;
struct Blc{
  int a[maxn][maxn];
  Blc(){memset(a,0,sizeof(a));}
}bas;
int head[maxn],cnt=0;
struct Edge{
  int nxt,to;
}edge[maxn];

void add(int from,int to){
  edge[++cnt].nxt=head[from];edge[cnt].to=to;head[from]=cnt;
}
IL int o(int x){if(x%2)return x+1;return x-1;}
IL Blc X(Blc x,Blc y){
  Blc ans;
  for(int i=1;i<=2*m;i++){
    for(int j=1;j<=2*m;j++){
      for(int k=1;k<=2*m;k++){
        ans.a[i][j]+=x.a[i][k]*y.a[k][j]%MOD;
        ans.a[i][j]%=MOD;
      }
    }
  }return ans;
}
IL Blc q_pow(Blc x,int s){
  Blc ans=bas;
  while(s){
    if(s%2)ans=X(ans,x);
    x=X(x,x);
    s=s/2;
  }return ans;
}
int main(){
  scanf("%d%d%d%d%d",&n,&m,&t,&A,&B);
  for(int i=1;i<=m;i++){
    int x,y;scanf("%d%d",&x,&y);
    add(x,y);add(y,x);
  }
  Blc box;
  for(int u=0;u<n;u++){
    for(int i=head[u];i!=0;i=edge[i].nxt){
      int v=edge[i].to;
      for(int ii=head[v];ii!=0;ii=edge[ii].nxt){
	//cout<<"pr:"<<i<<' '<<ii<<endl;
	if(i==o(ii))continue;
	bas.a[i][ii]++;
      }
    }
  }
  //pr(bas);
  for(int i=head[A];i!=0;i=edge[i].nxt){box.a[1][i]++;}  

  Blc ans=q_pow(bas,t-2);

  ans=X(box,ans);

  for(int i=1;i<=2*m;i++){
    if(edge[i].to==B){out=(out+ans.a[1][i])%MOD;}
  }
  //cout<<endl;pr(ans);
  printf("%d\n",out);
  return 0;
}