洛谷 P2680 运输计划 解题报告

P2680 运输计划

题目背景

公元2044年,人类进入了宇宙纪元。

题目描述

公元2044年，人类进入了宇宙纪元。

\(L\)国有\(n\)个星球，还有\(n-1\)条双向航道，每条航道建立在两个星球之间，这\(n−1\)条航道连通了\(L\)国的所有星球。

小\(P\)掌管一家物流公司， 该公司有很多个运输计划，每个运输计划形如：有一艘物流飞船需要从\(u_i\)号星球沿最快的宇航路径飞行到\(v_i\)号星球去。显然，飞船驶过一条航道是需要时间的，对于航道\(j\)，任意飞船驶过它所花费的时间为\(t_j\)，并且任意两艘飞船之间不会产生任何干扰。

为了鼓励科技创新，\(L\)国国王同意小\(P\)的物流公司参与\(L\)国的航道建设，即允许小\(P\)把某一条航道改造成虫洞，飞船驶过虫洞不消耗时间。

在虫洞的建设完成前小\(P\)的物流公司就预接了\(m\)个运输计划。在虫洞建设完成后，这\(m\)个运输计划会同时开始，所有飞船一起出发。当这\(m\)个运输计划都完成时，小\(P\)的物流公司的阶段性工作就完成了。

如果小\(P\)可以自由选择将哪一条航道改造成虫洞， 试求出小\(P\)的物流公司完成阶段性工作所需要的最短时间是多少？

输入输出格式

输入格式：

第一行包括两个正整数\(n, m\)，表示\(L\)国中星球的数量及小\(P\)公司预接的运输计划的数量，星球从1到\(n\)编号。

接下来\(n-1\)行描述航道的建设情况，其中第\(i\)行包含三个整数\(a_i, b_i\)和\(t_i\)t ，表示第\(i\)条双向航道修建在\(a_i\)与 \(b_i\)两个星球之间，任意飞船驶过它所花费的时间为 \(t_i\) 。数据保证\(1≤a _i ,b_i ≤n\)且\(0≤t_i≤1000\)。

接下来\(m\)行描述运输计划的情况，其中第\(j\)行包含两个正整数\(u_j\)和\(v_j\) ，表示第\(j\)个运输计划是从\(u_j\)号星球飞往\(v_j\)号星球。数据保证\(1≤u_i,v_i≤n\)

输出格式：

一个整数，表示小\(P\)的物流公司完成阶段性工作所需要的最短时间。

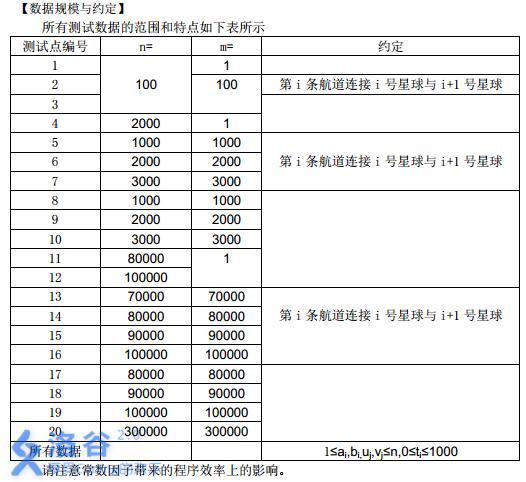
说明：

---

首先简化一下问题模型：对于询问的m条链中，删去一条边，使最大链最小。

妥妥的二分答案了，但是我做的时候并没有想简化模型，自然也没有想到二分答案，只是想到了贪心倍增的做法但是太难写，我估计写不出来。

下面说说二分答案。我们二分最大链长\(l\)。

对于链长小于等于\(l\)的，我们不管它。

对于链长大于\(l\)的，我们得确保删去的那条边在每条这样的链上，换而言之，我们要统计当前每条边的经历的链数。

我们找到合法的最大边，看看减去它后是否能使所有链长小于\(l\)。

那么现在还有两个问题，如何找到链和如何统计每条边经历的链数。

找到链即先预处理每条链的最近公共祖先，存储为三元组并带上链长。可以用\(tarjan\)直接\(O(n)\)离线处理了

统计链数时，我们发现也是离线操作而且没有修改。直接树上差分即可。

树上差分：思想与链上差分差不多，对三元组\((f,v1,v2)\)(\(f\)是后面两个祖先)，维护\(f\)的差分数组减去2，\(v1,v2\)的加上1。自下往上统计前缀和即是边的经历次数。

---

code:

#include <cstdio>
#include <cstring>
int max(int x,int y){return x>y?x:y;}
const int N=300010;
int n,m;
int read()
{
    char c=getchar();int x=0;
    while(c<'0'||c>'9') c=getchar();
    while(c>='0'&&c<='9') {x=x*10+c-'0';c=getchar();}
    return x;
}
struct Edge{int to,next,w;}edge[N<<1];
struct node{int to,next;}lca[N<<1];
int head[N],cnt=0,headl[N],cntl=0,dis[N],used[N],f[N],l=0,r=0;
void add(int u,int v,int w){edge[++cnt].next=head[u];edge[cnt].to=v;edge[cnt].w=w;head[u]=cnt;}
void addl(int u,int v){lca[++cntl].next=headl[u];lca[cntl].to=v;headl[u]=cntl;}
void dfs(int now)
{
    used[now]=1;
    for(int i=head[now];i;i=edge[i].next)
    {
        int v=edge[i].to,w=edge[i].w;
        if(!used[v])
        {
            dis[v]=dis[now]+w;
            dfs(v);
        }
    }
}
int find(int x){return f[x]=f[x]==x?x:find(f[x]);}
void merge(int x,int y){f[find(y)]=find(x);}
struct lc{int v[2],w,next;}d[N];int headlc[N],cntlc=0;
void addlc(int u,int w,int v1,int v2){d[++cntlc].w=w;d[cntlc].v[0]=v1;d[cntlc].v[1]=v2;d[cntlc].next=headlc[u];headlc[u]=cntlc;}
void LCA(int now)
{
    used[now]=1;
    for(int i=head[now];i;i=edge[i].next)
    {
        int v=edge[i].to;
        if(!used[v])
        {
            used[v]=1;
            LCA(v);
            merge(now,v);
        }
    }
    for(int i=headl[now];i;i=lca[i].next)
    {
        int v=lca[i].to;
        if(used[v])
        {
            int f0=find(v);
            int w=dis[v]-dis[f0]+dis[now]-dis[f0];
            r=max(r,w);
            addlc(f0,w,v,now);
        }
    }
}
void init()
{
    dfs(1);//预处理两点间长度
    int a,b;
    for(int i=1;i<=m;i++)
    {
        a=read(),b=read();
        addl(a,b);
        addl(b,a);
    }
    memset(used,0,sizeof(used));
    for(int i=1;i<=n;i++) f[i]=i;
    LCA(1);//两点间距离及最近公共祖先
}
int p_d[N],cntline=0,sum[N],m_max=0,m_maxl=0;
void dfs0(int now,int dist)
{
    used[now]=1;
    for(int i=head[now];i;i=edge[i].next)
    {
        int v=edge[i].to,w=edge[i].w;
        if(!used[v])
        {
            dfs0(v,w);
            sum[now]+=sum[v];
        }
    }
    sum[now]+=p_d[now];
    if(sum[now]==cntline)
        m_max=max(m_max,dist);
}
bool check(int c)
{
    memset(p_d,0,sizeof(p_d));
    cntline=0,m_max=0,m_maxl=0;
    for(int i=1;i<=n;i++)
        for(int j=headlc[i];j;j=d[j].next)
            if(d[j].w>c)
            {
                p_d[i]-=2;
                p_d[d[j].v[0]]++;
                p_d[d[j].v[1]]++;
                m_maxl=max(m_maxl,d[j].w);
                cntline++;
            }
    memset(used,0,sizeof(used));
    memset(sum,0,sizeof(sum));
    dfs0(1,0);
    return m_max+c>=m_maxl;
}
int main()
{
    n=read(),m=read();
    int u,v,w;
    for(int i=1;i<n;i++)
    {
        u=read(),v=read(),w=read();
        l=max(l,w);
        add(u,v,w);
        add(v,u,w);
    }
    l=r-l;
    init();
    while(l<r)
    {
        int mid=l+r>>1;
        if(check(mid))
            r=mid;
        else
            l=mid+1;
    }
    printf("%d\n",l);
    return 0;
}

其实这个代码\(N\)改成450,000再吸一波氧才能过。但我始终没弄清楚到底\(N\)开300,000到底是哪里\(RE\)了，有哪位大哥发现了评论一下呗~

2018.6.7