单源最短路径算法：迪杰斯特拉 (Dijkstra) 算法（一）

一、算法介绍

　　迪杰斯特拉算法（英语：Dijkstra's algorithm）由荷兰计算机科学家艾兹赫尔·迪杰斯特拉在1956年提出。迪杰斯特拉算法使用了广度优先搜索解决赋权有向图的单源最短路径问题。这个算法是通过为每个顶点 v 保留当前为止所找到的从s到v的最短路径来工作的。

　　初始时，原点 src 的路径权重被赋为 0 （dist[src] = 0）。若对于顶点 m 存在能直接到达的边（src, m），则把d[m]设为w（src, m）,同时把所有其他（src不能直接到达的）顶点的路径长度设为无穷大，即表示我们不知道任何通向这些顶点的路径（对于所有顶点的集合 V 中的任意顶点 v， 若 v 不为 src 和上述 m 之一， dist[v] = ∞）。当算法结束时，dist[v] 中存储的便是从 src 到 v 的最短路径，或者如果路径不存在的话是无穷大。

　　边的拓展是 Dijkstra 算法的基础操作：如果存在一条从 u 到 v 的边，那么从 src 到 v 的最短路径可以通过将边（u, v）添加到从 src 到 u 的路径尾部来拓展一条从 src 到 v 的路径。这条路径的长度是 dist[u] + w(u, v)。如果这个值比当前已知的 dist[v] 的值要小，我们可以用新的最小值来替代当前 dist[v] 中的值。拓展边的操作一直运行到所有的 dist[v] 都代表从 src 到 v 的最短路径的长度值。此算法的组织令 dist[u] 达到其最终值时，每条边（u, v）都只被拓展一次。

二、Dijkstra算法步骤

　　以下是 Dijkstra 算法中用于查找从单个源顶点到给定图中所有其他顶点的最短路径的详细步骤。

　　1）创建一个集合sptSet（最短路径树集合），该集合跟踪最短路径树中包含的顶点，即，其与源点的最小距离已被计算并确定。最初，此集合为空。

　　2）将距离值分配给输入图中的所有顶点。将所有距离值初始化为无穷大。将源顶点的距离值指定为0（dist[src] = 0），以便首先选择它。

　　3）虽然当前的 sptSet （表示最短路径树）并不包含所有顶点：

• 选择一个顶点 u，该顶点在 sptSet 中不存在，并且具有最小距离值。

• 将u包含到 sptSet 中。

• 更新u的所有相邻顶点的距离值。要更新距离值，要遍历所有相邻的顶点。对于每个相邻顶点 v，如果u（来自源点）的距离值和边缘u-v的权重之和小于v的距离值（dist[u] + graph[u][v] < dist[v]），则更新v的距离值。

　　下面来看一个例子：

　　集合 sptSet[] 最初为空，并且分配给每个顶点的距离为 dist[] = {0，INF，INF，INF，INF，INF，INF，INF}，其中INF表示无穷大。 现在选择具有最小距离值的顶点。 选择顶点0，将其包含在 sptSet 中。 因此，sptSet 变为 {0}。 将 0 包含到 sptSet 之后，更新其相邻顶点的距离值。 0 的相邻顶点是 1 和 7。1 和 7 的距离值被更新为 4 和 8。下面的子图显示了顶点及其距离值，仅显示了具有有限距离值的顶点。 最短路径树中包含的顶点显示为绿色。

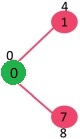
　　选择具有最小距离值且尚未包含在最短路径树中的顶点（不在 sptSet 中）。 选择 顶点1 并将其添加到 sptSet。 因此，sptSet 现在变为 {0，1}。 更新相邻顶点的距离值1。顶点2 的距离值变为 12。

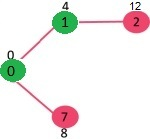
　　选择具有最小距离值且尚未包含在最短路径树中的顶点（不在 sptSet 中）。 选择了顶点7。 因此，sptSet 现在变为 {0，1，7}。 更新相邻 顶点7 的距离值。顶点 6 和 8 的距离值变得有限（分别为 15 和 9）。

　　选择具有最小距离值且尚未包含在最短路径树中的顶点（不在 sptSet 中）。选择了顶点6。因此，sptSet现在变为 {0，1，7，6}。更新相邻 顶点6 的距离值。更新顶点 5 和 8 的距离值。

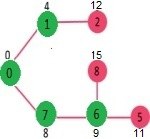
　　重复上述步骤，直到 sptSet 确实包含给定图的所有顶点。最后，我们得到以下最短路径树：

三、实现代码

　　下面是使用了邻接矩阵的迪杰斯特拉算法实现。其算法的时间复杂度为 O(V²)。

 1     /**
 2      * 为使用邻接矩阵表示的图实现Dijkstra的单源最短路径算法的函数
 3      *
 4      * @param graph 地图，给出的邻接矩阵
 5      * @param src 源顶点
 6      */
 7     public void dijkstra(int[][] graph, int src) {
 8         /* 输出数组，dist[i]将保存从src到i的最短距离 */
 9         int[] dist = new int[V];
10
11         /* 如果顶点i包含在最短路径树中或从src到i的最短距离已确定，则sptSet[i]将为true */
12         Boolean[] sptSet = new Boolean[V];
13
14         /* 将所有距离初始化为无穷大并将stpSet[]初始化为false */
15         for (int i = 0; i < V; i++) {
16             dist[i] = Integer.MAX_VALUE;
17             sptSet[i] = false;
18         }
19
20         /* 源顶点与其自身的距离始终为0 */
21         dist[src] = 0;
22
23         /* 查找所有顶点的最短路径 */
24         for (int count = 0; count < V - 1; count++) {
25             int u = minDistance(dist, sptSet);
26
27             /* 将选取的顶点标记为已处理 */
28             sptSet[u] = true;
29
30             /* 更新选取的顶点的相邻顶点的dist值。*/
31             for (int v = 0; v < V; v++) {
32                 /* 仅当不在sptSet中标记过且在u到v之间存在边且从src到通过u的v的路径的总权重小于dist[v]的当前值时，
33                     才更新dist [v]。*/
34                 if (!sptSet[v] && graph[u][v] != 0 && dist[u] != Integer.MAX_VALUE && dist[u] + graph[u][v] < dist[v]) {
35                     dist[v] = dist[u] + graph[u][v];
36                 }
37             }
38         }
39
40         /* 打印构造的最短距离数组 */
41         printSolution(dist);
42     }

　　函数 minDistance()，从尚未包含在最短路径树中的一组顶点中查找具有最小距离值的顶点，就是算法从已知的最短路径树外选取距离远点比较近的顶点来进行边的扩展。此函数的时间复杂度为 O(V)。

 1     /**
 2      * 从尚未包含在最短路径树中的一组顶点中查找具有最小距离值的顶点
 3      *
 4      * @param dist 存当前距离源点的最短路径
 5      * @param sptSet 顶点是否存在于最短路树中
 6      * @return
 7      */
 8     public int minDistance(int[] dist, Boolean[] sptSet) {
 9         /* 初始化最小值 */
10         int min = Integer.MAX_VALUE;
11         int min_index = -1;
12
13         for (int v = 0; v < V; v++) {
14             if (!sptSet[v] && dist[v] <= min) {
15                 min = dist[v];
16                 min_index = v;
17             }
18         }
19
20         return min_index;
21     }