LeetCode---84. 柱状图中最大的矩形(hard)

题目：84. 柱状图中最大的矩形

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

示例:

输入: [2,1,5,6,2,3]

输出: 10

---

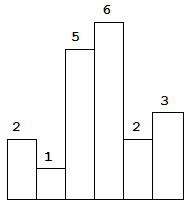
我们要求的是能勾勒出来的最大矩形面积

先用暴力破解整理一下思路，可以这样来做，循环遍历每根柱子，以每根柱子为高，不断向两边扩散直到遇到高度比自己低的柱子为止，求出最大面积

//核心代码如下
//从左往右遍历每根柱子
for (int i = 0; i < heights.length; i++) {
    int w = 1;
    int j = i - 1;
    //向左扩散，直到遇到比自己高度低的柱子，宽度不断加一
    while (j >= 0) {
        if (heights[j] < heights[i]) {
            break;
        }else {
            w++;
            j--;
        }
    }
    j = i + 1;
    //向右遍历，直到遇到比自己低的柱子，宽度继续增加
    while (j < heights.length) {
        if (heights[j] < heights[i]) {
            break;
        }else {
            w++;
            j++;
        }
    }
    //计算出来以这根柱子为高所能勾勒出来的面积，再比较赋值
    maxArea = Math.max(maxArea,heights[i] * w);
}

每根柱子都会向左向右扩散，这样就造成了很多的重复，时间复杂度为O(N²)，会超时

这时候再想能不能优化一下，使用更少的时间来解决问题

当使用暴力破解的时候，我们从左往右遍历每一根柱子进行求值

  因为柱子是从左边开始遍历过来的，所以遍历到某值时它左边的所有柱子的高度其实已经被遍历过了，所以我们可以用一个有序的栈来存储左边柱子的值，在这里我们使用递增的栈来存储左边元素

  当我们遍历到比栈顶元素高度更低的柱子时(反之，则入栈)，说明以当前高度已经无法向右边扩撒了，而因为栈中元素是递增的，所以左边能扩散到的宽度就是到栈中的上一个元素 (先忽略柱子高度相等的情况)，那么栈顶元素所能勾勒出来的最大矩形面积就可以求出来了

我们通过代码来进一步理解

class Solution {
    public int largestRectangleArea(int[] heights) {
        // 使用栈解决
        // 注意：栈里面存储的是下标值，因为高度可以由下标值得出
        int res = 0;
        int len = heights.length;
        Deque<Integer> stack = new ArrayDeque<>();

        // 从左往右遍历每一根柱子
        for (int i = 0; i < len; i++) {
           // 当此时栈顶元素对应柱子的高度大于正在遍历的柱子高度时，进入循环
            while (!stack.isEmpty() && heights[stack.peekLast()] > heights[i]) {
                // 得出栈顶柱子的高度，并且将起弹出栈
                int h = heights[stack.pollLast()];

                // 特殊情况，如果现在栈顶柱子的高度与刚弹出栈的柱子的高度相等，那么将其弹出栈
                while (!stack.isEmpty() && heights[stack.peekLast()] == h) {
                    stack.removeLast();
                }

                // w 是所求柱子的宽度，如果栈不为空，它就等于 i 的值减去现在栈顶的值再减一
                int w = 0;
                if (stack.isEmpty()){
                    w = i;
                } else {
                    w = i - stack.peekLast() - 1;
                }
                res = Math.max(res, h * w);
            }
            stack.addLast(i);
        }

        // 此时栈中可能仍有元素，我们需要计算出以每根柱子为高能勾勒出最大的矩形面积，所以需要将所有元素都弹出栈
        while (!stack.isEmpty()) {
            int h = heights[stack.pollLast()];
            int w = 0;
            if (stack.isEmpty()) {
                w = len;
            } else {
                w = len - stack.peekLast() - 1;
            }
            res = Math.max(res, h * w);
        }
        return res;
    }
}

此时本题已经完成，但我们仍然可以继续进行优化---加入哨兵

比如说 [2,1,5,6,2,3] 是我们要求的柱状图，我们可以在数组的两端都插入 0 ，也就是在原先柱状图的基础上，在两端插入分别插入一个高度为0的柱子，变成[0,2,1,5,6,2,3,0]，这样 0 就成为了最小的高度，那么遍历元素结束的时候，所有元素都可以弹出栈，就不用再考虑遍历完栈不为空的情况了

代码:

class Solution {
    public int largestRectangleArea(int[] heights) {
        // 加入哨兵进行优化
        int res = 0;
        int len = heights.length;
        int[] newHeights = new int[len+2];
        newHeights[0] = 0;
        System.arraycopy(heights,0,newHeights,1,len);
        heights = newHeights;
        Deque<Integer> stack = new ArrayDeque<>();
        stack.addLast(newHeights[0]);
        len = len + 2;
        for (int i = 1; i < len; i++) {
            while (heights[i] < heights[stack.peekLast()]) {
                int h = heights[stack.pollLast()];
                int w = i - stack.peekLast() - 1;
                res = Math.max(res, h * w);
            }
            stack.addLast(i);
        }
        return res;
    }
}