各类分布----二项分布，泊松分布，负二项分布，gamma 分布，高斯分布，学生分布，Z分布

伯努利实验：

如果无穷随机变量序列  是独立同分布(i．i．d．)的，而且每个随机变量  都服从参数为p的伯努利分布，那么随机变量  就形成参数为p的一系列伯努利试验。同样，如果n个随机变量  独立同分布，并且都服从参数为p的伯努利分布，则随机变量  形成参数为p的n重伯努利试验。

伯努利试验是只有两种可能结果的单次随机试验。

• 如果试验E是一个伯努利试验，将E独立重复地进行n次，则称这一串重复的独立试验为n重伯努利试验。

一、伯努利分布：

伯努利分布亦称“零一分布”、“两点分布”。称随机变量X有伯努利分布, 参数为p(0<p<1),如果它分别以概率p和1-p取1和0为值。EX= p,DX=p(1-p)。伯努利试验成功的次数服从伯努利分布,参数p是试验成功的概率。伯努利分布是一个离散型机率分布，是N=1时二项分布的特殊情况，为纪念瑞士科学家詹姆斯·伯努利(Jacob Bernoulli 或James Bernoulli)而命名。

例子：假定重复抛掷一枚均匀硬币，如果在第i次抛掷中出现正面，令  ；如果出现反面，令  ，那么，随机变量  就形成参数为  的一系列伯努利试验，同样，假定由一个特定机器生产的零件中10%是有缺陷的，随机抽取n个进行观测，如果第i个零件有缺陷，令 ；如果没有缺陷，令  ，那么，随机变量  就形成参数为  的n重伯努利试验 （百度百科）

E(X)=p， E(X²)=q ， Var(X)=pq

二、二项分布：

n 次Bernoulli试验的结果中，每次试验的分布不变，结果为1的次数 X 的分布。就是重复n次的伯努利实验。

在概率论和统计学里面，带有参数n和p的二项分布表示的是n次独立试验的成功次数的概率分布。在每次独立试验中只有取两个值，表示成功的值的概率为p，那么表示试验不成功的概率为1-p。这样一种判断成功和失败的二值试验又叫做伯努利试验。

特殊地，当n=1的时候，我们把二项分布称为伯努利分布。

如果

1．在每次试验中只有两种可能的结果，而且是互相对立的；

2．每次实验是独立的，与其它各次试验结果无关；

3．结果事件发生的概率在整个系列试验中保持不变，则这一系列试验称为伯努利实验。

在这试验中，事件发生的次数为一随机事件，它服从二次分布

 

三、超几何分布：

超几何分布，n 次伯努利试验，每次试验分布发生改变，结果为1的次数 X  的分布，当试验分布变化不大的时候和二项分布结果相同
它描述了从有限N个物件（其中包含M个指定种类的物件）中抽出n个物件，成功抽出该指定种类的物件的次数（不放回）

四、泊松分布

泊松分布就是描述某段时间内，事件具体的发生概率。

泊松分布的概率函数为：

泊松分布的参数λ是单位时间(或单位面积)内随机事件的平均发生次数。 泊松分布适合于描述单位时间内随机事件发生的次数。

k事件X发生的频数；P（X=k）事件X发生k次的概率

泊松分布的期望和方差均为 

特征函数为 

当二项分布的n很大而p很小时，泊松分布可作为二项分布的近似，其中λ为np。通常当n≧20,p≦0.05时，就可以用泊松公式近似得计算，当n趋近于无穷的时候等同于二项分布。

五、多项分布

是二项式分布的推广。二项式做n次伯努利实验，规定了每次试验的结果只有两个，如果现在还是做n次试验，只不过每次试验的结果可以有多m个，且m个结果发生的概率互斥且和为1，则发生其中一个结果X次的概率就是多项式分布。

扔骰子是典型的多项式分布。扔骰子，不同于扔硬币，骰子有6个面对应6个不同的点数，这样单次每个点数朝上的概率都是1/6（对应p1~p6，它们的值不一定都是1/6，只要和为1且互斥即可，比如一个形状不规则的骰子）,重复扔n次，如果问有k次都是点数6朝上的概率。

六、负二项分布

一种离散概率分布。满足以下条件的称为负二项分布：实验包含一系列独立的实验， 每个实验都有成功、失败两种结果，成功的概率是恒定的，实验持续到r次成功，r为正整数。

当r是整数时，负二项分布又称帕斯卡分布（巴斯卡分布），其概率质量函数为（其中一种形式，两种形式对比看下文）：

它表示，已知一个事件在伯努利试验中每次的出现概率是p，在一连串伯努利试验中，一件事件刚好在第r + k次试验出现第r次的概率。

参数为(r, p)的负二项分布的数列k+r的期望是  。

七、gamma分布

是统计学的一种连续概率函数。

gamma函数定义：

Γ(x) = ∫₀^∞ t^x-1 e^-t dt                      Γ(x+1) = x Γ(x);              Γ(x+1) = x!

Gamma分布中的参数α称为形状参数（shape parameter），β称为逆尺度参数（scale parameter）

假设随机变量X为等到第α件事发生所需之等候时间, 密度函数为

              

特征函数为

 

伽马分布的概率密度函数和失效率函数取决于形状参数

 

的数值。

当

  

时，

 

为递减函数；

当

  

时，

  

为递增函数；

当  时，

  

为单峰函数；

Gamma的可加性

两个独立随机变量X和Y，且X~Ga(a,γ），Y~Ga(b,γ），则Z = X+Y ~ Ga(a+b,γ）。注意X和Y的尺度参数必须一样。

Gamma分布的特殊形式

当形状参数α=1时，伽马分布就是参数为γ的指数分布，X~Exp（γ）

当α=n/2，β=1/2时，伽马分布就是自由度为n的卡方分布，X^2(n)

β=n，Γ(n,α)就是Erlang分布。Erlang分布常用于可靠性理论和排队论中 ,如一个复杂系统中从第 1 次故障到恰好再出现 n 次故障所需的时间;从某一艘船到达港口直到恰好有 n 只船到达所需的时间都服从 Erlang分布；

八、指数分布

指数分布是事件的时间间隔的概率。如：

• 婴儿出生的时间间隔

• 来电的时间间隔

• 奶粉销售的时间间隔

• 网站访问的时间间隔

是描述泊松过程中的事件之间的时间的概率分布，即事件以恒定平均速率连续且独立地发生的过程。 这是伽马分布的一个特殊情况，它是几何分布的连续模拟，它具有无记忆的关键性质。

指数函数的一个重要特征是无记忆性（Memoryless Property，又称遗失记忆性）。这表示如果一个随机变量呈指数分布，当s,t>0时有P(T>t+s|T>t)=P(T>s)。即，如果T是某一元件的寿命，已知元件使用了t小时，它总共使用至少s+t小时的条件概率，与从开始使用时算起它使用至少s小时的概率相等。

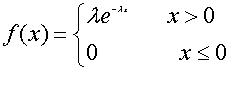
期望值： ，方差：                若随机变量x服从参数为λ的指数分布，则记为  。

九、卡方分布

若n个相互独立的随机变量ξ₁，ξ₂，...,ξn ，均服从标准正态分布（也称独立同分布于标准正态分布），则这n个服从标准正态分布的随机变量的平方和 构成一新的随机变量，其分布规律称为卡方分布（chi-square distribution）。其中参数  称为自由度。记为  或者  （其中  ，  为限制条件数）。

卡方分布是由正态分布构造而成的一个新的分布，当自由度 很大时，  分布近似为正态分布。

1)  分布在第一象限内，卡方值都是正值，呈正偏态（右偏态），随着参数  的增大，  分布趋近于正态分布；卡方分布密度曲线下的面积都是1.

2)  分布的均值与方差可以看出，随着自由度 的增大，χ2分布向正无穷方向延伸（因为均值  越来越大），分布曲线也越来越低阔（因为方  越来越大）。

3）不同的自由度决定不同的卡方分布，自由度越小，分布越偏斜。

4) 若  互相独立，则：

  

服从

  

分布，自由度为

  

5)  分布的均数为自由度

 

，记为 E(

  

) =

  

。

6)  分布的方差为2倍的自由度(

  

)，记为 D(

  

) =

  

十、Beta分布

B函数，又称为Beta函数或者第一类欧拉积分，是一个作为伯努利分布和二项式分布的共轭先验分布的密度函数，是指一组定义在(0,1) 区间的连续概率分布，定义如下：

有两个参数  

Β分布的概率密度函数是：

 

其中  

是Γ函数。随机变量X服从参数为

 

的Β分布通常写作

 

Β分布的累积分布函数是 [1]  ：

 

其中

 

是不完全Β函数，

  

是正则不完全贝塔函数。

 

Beta分布与Gamma分布的关系为：

实例：

空气中含有的气体状态的水分。表示这种水分的一种办法就是相对湿度。即现在的含水量与空气的最大含水量（饱和含水量）的比值。我们听到的天气预告用语中就经常使用相对湿度这个名词。

相对湿度的值显然仅能出现于0到1之间（经常用百分比表示）。而空气为什么出现某个相对湿度显然具有随机性（可以利用最复杂原理），这些提示我们空气的相对湿度可能符合贝塔分布。

十一、几何分布

是离散型概率分布。在n次伯努利试验中，试验k次才得到第一次成功的机率。详细地说，是：前k-1次皆失败，第k次成功的概率。几何分布是帕斯卡分布当r=1时的特例。

在伯努利试验中，记每次试验中事件A发生的概率为p，试验进行到事件A出现时停止，此时所进行的试验次数为X，其分布列为：

此分布列是几何数列的一般项，因此称X服从几何分布，记为X ～ GE(p) 。

实际中有不少随机变量服从几何分布，譬如，某产品的不合格率为0.05，则首次查到不合格品的检查次数X ～ GE(0.05) 。

它分两种情况：

（1）为得到1次成功而进行n次伯努利试验，n的概率分布，取值范围为1，2，3，...；

这种情况的期望和方差如下：

（2）m = n-1次失败，第n次成功，m的概率分布，取值范围为0，1，2，3，...。

这种情况的期望和方差如下：

比如，假设不停地掷骰子，直到得到1。投掷次数是随机分布的，取值范围是无穷集合{ 1, 2, 3, ... }，并且是一个p= 1/6的几何分布。

十二、学生分布（t分布）

用于根据小样本来估计呈正态分布且方差未知的总体的均值。如果总体方差已知（例如在样本数量足够多时），则应该用正态分布来估计总体均值。

t分布曲线形态与n（确切地说与自由度df）大小有关。与标准正态分布曲线相比，自由度df越小，t分布曲线愈平坦，曲线中间愈低，曲线双侧尾部翘得愈高；自由度df愈大，t分布曲线愈接近正态分布曲线，当自由度df=∞时，t分布曲线为标准正态分布曲线。

由于在实际工作中，往往σ是未知的，常用s作为σ的估计值，为了与u变换区别，称为t变换，统计量t 值的分布称为t分布。[1] 

假设X服从标准正态分布N（0,1），Y服从  分布，那么

  

的分布称为自由度为n的t分布,记为

  

。

分布密度函数

  

，其中，Gam(x)为伽马函数。

十三、正态分布

正态曲线呈钟型，两头低，中间高，左右对称因其曲线呈钟形，因此人们又经常称之为钟形曲线。

若随机变量X服从一个数学期望为μ、方差为σ^2的正态分布，记为N(μ，σ^2)。其概率密度函数为正态分布的期望值μ决定了其位置，其标准差σ决定了分布的幅度。当μ = 0,σ = 1时的正态分布是标准正态分布。

十四、狄利克雷分布

狄利克雷分布(Dirichlet distribution)是多项分布的共轭分布，也就是它与多项分布具有相同形式的分布函数。同时可以看做是将Beta分布推广到多变量的情形。一类在实数域以正单纯形（standard simplex）为支撑集（support）的高维连续概率分布，是Beta分布在高维情形的推广。

对独立同分布（independent and identically distributed, iid）的连续随机变量  和支撑集 ，若 服从狄利克雷分布，则其概率密度函数

  

有如下定义 [1]  ：

 

式中，  是无量纲的分布参数，

  

是分布参数的和，

  

是多元Beta函数（multivariate beta function），

  

为Gamma函数。由上述解析形式可知，狄利克雷分布是指数族分布 [1]  。

应用

在贝叶斯推断中，狄利克雷分布作为多项分布的共轭先验，被用于多项分布、二项分布和类型分布（categorical distribution）的参数估计 [1]  。在机器学习领域，狄利克雷分布和广义狄利克雷分布被应用于构建混合模型（mixture model）以处理高维的聚类和特征赋权（feature weighting）等非监督学习问题 [21]  。使用狄利克雷分布建立的主题模型（topic model），即隐含狄利克雷分布（Latent Dirichlet Allocation, LDA）被应用于自然语言处理（Natural Language Processing, NLP）和生物信息学研究（bioinfomatics）

泊松分布和负二项分布用途区分

https://www.jianshu.com/p/ad24bb90b972
---------------------
原文：https://blog.csdn.net/tonyshengtan/article/details/82947416