Support Vector Machine(2)：Lagrange Duality求解线性可分SVM的最佳边界

在上篇文章《Support Vector Machine(1):线性可分集的决策边界》中，我们最后得到，求SVM最佳Margin的问题，转化为了如下形式：

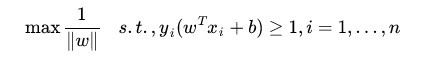
到这一步后，我个人又花了很长的时间去查阅资料，因为数学较差的原因，理解起来相当慢，不过探索的乐趣也就在于不断的打破瓶颈向前，OK继续。上述的问题等价于：

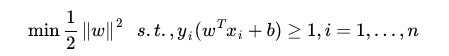
而后我们引入广义拉格朗日函数，利用拉格朗日对偶性来求解此问题。首先明确一下，我们做这些工作的目的是，消去约束条件，为了好求解问题。广义拉格朗日函数为：

上式分为两部分，拉格朗日前辈的思路是，让后一项达到最大值，然后固定住，则问题等价于求前一项的最小值。既然我们想要消去条件（第二项），那么就要证明条件是没用的。也就是说，无论给不给出，这个条件都会成立，那必然就可以舍弃！所以说来，我们考虑，这个世界上只存在两种可能：

　　

首先，我们考虑<1的情况，即不满足原问题的条件，则广义拉格朗日函数的第二项，其最大值会趋于无穷，那么我们没法求该式子的最小值，这个条件也就会被放弃！而在大于等于一的情况下，函数的第二项会趋向于0，也就是说，当我们求整个公式的最小值时，会天然的选择满足条件的一侧，从而将原问题转化为：

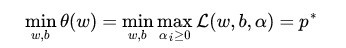
然后我们考虑下一个问题，对偶。刚才，我们先把着眼点放在第二项上，将其最大化，然后再将第一项最小化从而转化了原问题。那么，如果我们再看一下这个公式：如果将alpha视为常量（取为alpha'），然后将w和b作为变量来最小化这个函数，可知第二项小于等于第一次我们推导的公式。为什么，因为刚才我们把第二项做了max，而现在却是取为alpha'，max>=any。也即：

现在确定了w和b，我们再将alpha'来做变换，取最大值，可知：

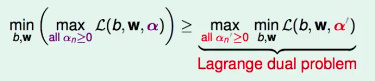
由此得到拉格朗日对偶问题(Lagrange Dual Problem)。

在一般条件下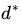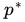，≤，但在某些特殊情况下，二者却是等价的，这种情况叫做强对偶。而我们求解SVM的最佳边界，就要用强对偶下的KKT(Karush–Kuhn–Tucker conditions)条件来完成。KKT条件如下：

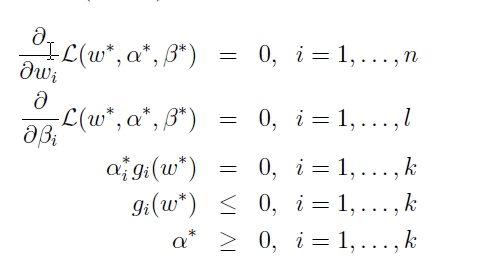
在第三个条件中，我们如果回想，g(w)是什么？可以依稀记得：

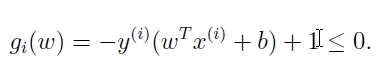
也就是说，此处令alpha>0即g(w)=0的解，是在我们的margin(s)上的，即它们就是support vectors

求解步骤：

1、固定住alpha，对w和b分别求偏导数，让其等于0：

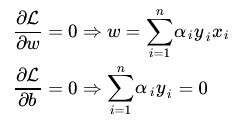
带回之前的L，得到：

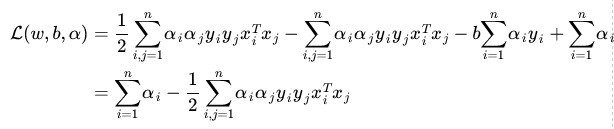
推导过程如下：

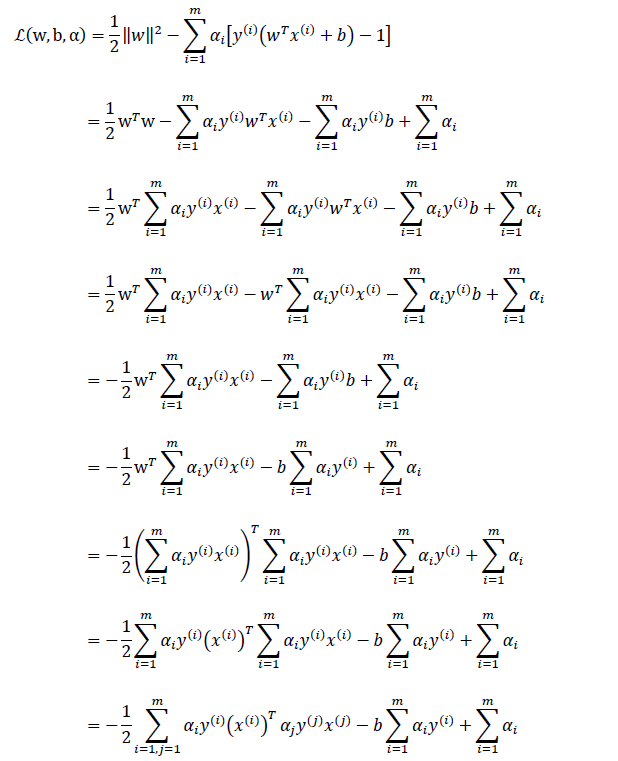
一定要注意x是转置的。为什么a和y不转置？因为a是常数呀，y呢？y是分类呀，-1或者1，所以无需转置。则问题转化为：

利用SMO继续求解的过程，请见：SMO算法

---------------------------------------------------------------------------------------------------------------------------------------

声明几点：

1、要特别感谢这篇文章：简易解说拉格朗日对偶（Lagrange duality），特别喜欢这种平易近人的数学讲解。

2、支持向量机通俗导论写的相当详尽，个人拜读了不下20遍，依然在继续学习中。

3、李航老师的《统计学习方法》中，也讲的很透彻。

我是个看到类似‘拉格朗日’这种字眼就害怕的人，拜谢前人的智慧和分享精神。