Stanford机器学习笔记-10. 降维(Dimensionality Reduction)

10. Dimensionality Reduction

Content 

10. Dimensionality Reduction

　　10.1 Motivation

　　　　10.1.1 Motivation one: Data Compression

　　　　10.2.2 Motivation two: Visualization

　　10.2 Principal Component Analysis

　　　　10.2.1 Problem formulation

　　　　10.2.2 Principal Component Analysis Algorithm

　　　　10.2.3 Choosing the Number of Principal Components

　　　　10.2.4 Advice for Applying PCA

10.1 Motivation

10.1.1 Motivation one: Data Compression

如果我们有许多冗余的数据，我们可能需要对特征量进行降维(Dimensionality Reduction)。

我们可以找到两个非常相关的特征量，可视化，然后用一条新的直线来准确的描述这两个特征量。例如图10-1所示，x1和x2是两个单位不同本质相同的特征量，我们可以对其降维。

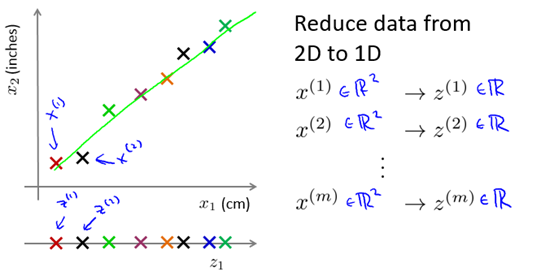
图10-1 一个2维到1维的例子

又如图10-2所示的3维到2维的例子，通过对x1,x2,x3的可视化，发现虽然样本处于3维空间，但是他们大多数都分布在同一个平面中，所以我们可以通过投影，将3维降为2维。

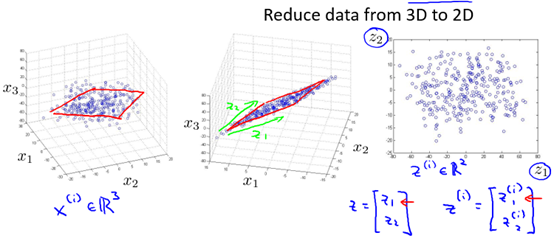
图10-2 一个3维到2维的例子

降维的好处很明显，它不仅可以数据减少对内存的占用，而且还可以加快学习算法的执行。

注意，降维只是减小特征量的个数(即n)而不是减小训练集的个数(即m)。

10.2.2 Motivation two: Visualization

我们可以知道，但特征量维数大于3时，我们几乎不能对数据进行可视化。所以，有时为了对数据进行可视化，我们需要对其进行降维。我们可以找到2个或3个具有代表性的特征量，他们(大致)可以概括其他的特征量。

例如，描述一个国家有很多特征量，比如GDP，人均GDP，人均寿命，平均家庭收入等等。想要研究国家的经济情况并进行可视化，我们可以选出两个具有代表性的特征量如GDP和人均GDP，然后对数据进行可视化。如图10-3所示。

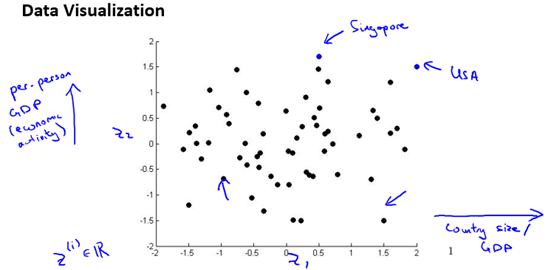
图10-3 一个可视化的例子

10.2 Principal Component Analysis

主成分分析(Principal Component Analysis : PCA)是最常用的降维算法。

10.2.1 Problem formulation

首先我们思考如下问题，对于正交属性空间(对2维空间即为直角坐标系)中的样本点，如何用一个超平面(直线/平面的高维推广)对所有样本进行恰当的表达？

事实上，若存在这样的超平面，那么它大概应具有这样的性质：

• 最近重构性 : 样本点到这个超平面的距离都足够近；
• 最大可分性：样本点在这个超平面上的投影能尽可能分开。

下面我们以3维降到2维为例，来试着理解为什么需要这两种性质。图10-4给出了样本在3维空间的分布情况，其中图(2)是图(1)旋转调整后的结果。在10.1节我们默认以红色线所画平面(不妨称之为平面s1)为2维平面进行投影(降维)，投影结果为图10-5的(1)所示，这样似乎还不错。那为什么不用蓝色线所画平面（不妨称之为平面s2）进行投影呢? 可以想象，用s2投影的结果将如图10-5的(2)所示。

图10-4 样本在3维正交空间的分布

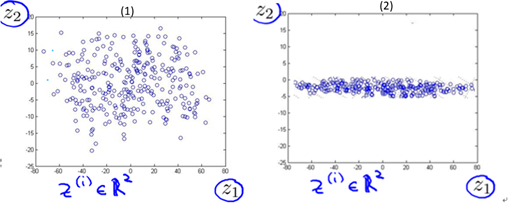
图10-5 样本投影在2维平面后的结果

由图10-4可以很明显的看出，对当前样本而言，s1平面比s2平面的最近重构性要好（样本离平面的距离更近）；由图10-5可以很明显的看出，对当前样本而言，s1平面比s2平面的最大可分性要好(样本点更分散)。不难理解，如果选择s2平面进行投影降维，我们会丢失更多（相当多）的特征量信息，因为它的投影结果甚至可以在转化为1维。而在s1平面上的投影包含更多的信息(丢失的更少)。

这样是否就是说我们从3维降到1维一定会丢失相当多的信息呢? 其实也不一定，试想，如果平面s1投影结果和平面s2的类似，那么我们可以推断这3个特征量本质上的含义大致相同。所以即使直接从3维到1维也不会丢失较多的信息。这里也反映了我们需要知道如何选择到底降到几维会比较好(在10.2.3节中讨论)。

让我们高兴的是，上面的例子也说明了最近重构性和最大可分性可以同时满足。更让人兴奋的是，分别以最近重构性和最大可分性为目标，能够得到PCA的两种等价推导。

一般的，将特征量从n维降到k维：

• 以最近重构性为目标，PCA的目标是找到k个向量，将所有样本投影到这k个向量构成的超平面，使得投影的距离最小（或者说投影误差projection error最小）。
• 以最大可分性为目标，PCA的目标是找到k个向量，将所有样本投影到这k个向量构成的超平面，使得样本点的投影能够尽可能的分开，也就是使投影后的样本点方差最大化。

注意: PCA和线性回归是不同的，如图10-6所示，线性回归是以平方误差和(SSE)最小为目标，参见1.2.4节；而PCA是使投影(二维即垂直)距离最小；PCA与标记或者预测值完全无关，而线性回归是为了预测y的值。

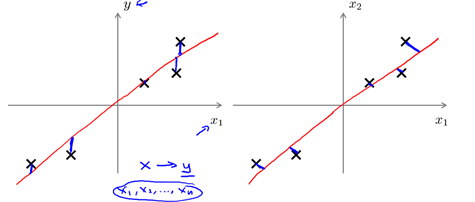
图10-6 PCA不是线性回归

分别基于上述两种目标的具体推导过程参见周志华老师的《机器学习》P230。两种等价的推导结论是：对协方差矩阵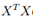进行特征值分解，将求得的特征值进行降序排序，再去前k个特征值对应的特征向量构成。

其中

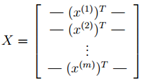
10.2.2 Principal Component Analysis Algorithm

基于上一节给出的结论，下面给出PCA算法。

输入：训练集：，低维空间维数k

过程：

1. 数据预处理：对所有样本进行中心化(即使得样本和为0)

   

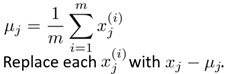
2. 计算样本的协方差矩阵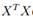（Sigma）

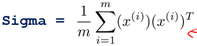       （其中是n*1的向量）

   在matlab中具体实现如下，其中X为m*n的矩阵：

   Sigma = (1/m) * X'* X;

3. 对2中求得的协方差矩阵Sigma进行特征值分解

   在实践中通常对协方差矩阵进行奇异值分解代替特征值分解。在matlab中实现如下：

   [U, S, V] = svd(Sigma); (svd即为matlab中奇异值分解的内置函数)

4. 取最大的k个特征值所对应的特征向量

   在matlab具体实现时，Ureduce = 认为是第3步求得的U的前k个，即有：Ureduce = U( : , 1:k); 其中Ureduce为n*k的矩阵

经过了上述4步得到了投影矩阵Ureduce，利用Ureduce就可以得到投影后的样本值

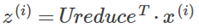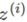（为k*1的向量）

下面总结在matlab中实现PCA的全部算法（假设数据已被中心化）

Sigma = (1/m) * X' * X;    % compute the covariance matrix

[U,S,V] = svd(Sigma);      % compute our projected directions

Ureduce = U(:,1:k);        % take the first k directions

Z = Ureduce' * X;          % compute the projected data points

10.2.3 Choosing the Number of Principal Components

如何选择k（又称为主成分的个数）的值？

首先，试想我们可以使用PCA来压缩数据，我们应该如何解压？或者说如何回到原本的样本值？事实上我们可以利用下列等式计算出原始数据的近似值Xapprox：

Xapprox = Z * Ureduce (m*n = m*k * k*n )

自然的，还原的数据Xapprox越接近原始数据X说明PCA误差越小，基于这点，下面给出选择k的一种方法：

结合PCA算法，选择K的算法总结如下：

这个算法效率特别低。在实际应用中，我们只需利用svd()函数，如下：

10.2.4 Advice for Applying PCA

1. PCA通常用来加快监督学习算法。
2. PCA应该只是通过训练集的特征量来获取投影矩阵Ureduce，而不是交叉检验集或测试集。但是获取到Ureduce之后可以应用在交叉检验集和测试集。
3. 避免使用PCA来防止过拟合，PCA只是对特征量X进行降维，并没有考虑Y的值；正则化是防止过拟合的有效方法。
4. 不应该在项目一开始就使用PCA: 花大量时间来选择k值，很可能当前项目并不需要使用PCA来降维。同时，PCA将特征量从n维降到k维，一定会丢失一些信息。
5. 仅仅在我们需要用PCA的时候使用PCA: 降维丢失的信息可能在一定程度上是噪声，使用PCA可以起到一定的去噪效果。
6. PCA通常用来压缩数据以加快算法，减少内存使用或磁盘占用，或者用于可视化(k=2, 3)。

参考：《机器学习》  周志华