PID控制器开发笔记之十一：专家PID控制器的实现

　　前面我们讨论了经典的数字PID控制算法及其常见的改进与补偿算法，基本已经覆盖了无模型和简单模型PID控制经典算法的大部。再接下来的我们将讨论智能PID控制，智能PID控制不同于常规意义下的智能控制，是智能算法与PID控制算法的结合，是基于PID控制器的智能化优化。

　　在本章我们首先来探讨一下专家PID算法。正如前面所说，专家PID算法是专家系统与PID算法的结合与应用优化，所以我们接下来先简单了解专家控制。

1、专家控制的基本思想

　　专家控制是智能控制的一个分支，是专家系统的理论和技术同控制理论、方法与技术相结合，在无对象模型的情况下，模仿领域专家的经验来实现对被控对象的控制。

　　专家控制一般由知识库和推理机构构成主体框架，按照某种策略及时选用恰当的规则进行推理输出，实现控制。其基本结构如下：

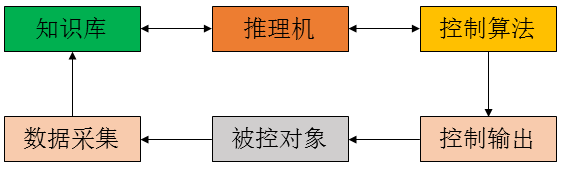
　　有上图我们不难发现影响专家控制器控制精确性的主要是知识库表达的准确性以及推理机的正确性。知识库越完备、越准确那么对你被控对像的状态识别也就越准确。当然，推理机设计的差别也会对控制结果有影响。

　　专家控制器一般来说分为2中实现形式，被称之为直接型专家控制器和间接型专家控制器。所谓直接型专家控制器就是用专门设计的专家控制器直接对被控对象进行控制的方法。该控制器任务和功能都比较简单，一般都是实时在线运行，直接对被控对象进行控制。其结构图如下：

　　而所谓间接型专家控制器是指专家控制器作为其他控制器的辅助方式或者相互结合的控制方式来实现的一种控制器。专家系统通过高层决策来影响控制器输出，而这种高层决策可以是在线也可以是离线，器不会直接控制被控对象。其结构图如下：

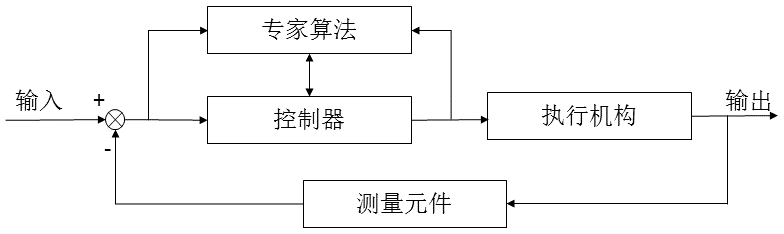
　　所以我们所要讨论的专家PID算法应该是一种直接型专家控制器，因为专家系统决策与PID算法是结合在一起的，并没有独于PID算法的专家控制器，而是专家决策直接决定PID算法机器输出，这与直接型专家控制的定义是相符的。

2、专家PID的设计思路

　　专家PID控制就是基于被控对象和控制规律的各种知识，而不需要知道被控对象的精确模型，利用专家经验来设计PID参数。怎么来实现这一过程呢？我们来分析并推导这一算法。

　　我们假设当前为第k采样，当前偏差为e(k)，同样前一采样时刻的偏差为e(k-1)，而前两个采样时刻的偏差为e(k-1)，则可以得到两次的偏差增量为：

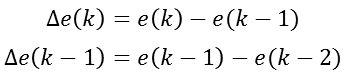
　　清楚了以上公式，我们再设定偏差的一个极大值，记为Mmax；设定一个偏差较大的中间值，记为Mmid；设定一个偏差的极小值，记为Mmin。根据以上偏差、偏差增量以及偏差极值的设定，我们分析如下：

（1）如果|e(k)|>Mmax

　　这种情况说明偏差的绝对值已经很大了，不论偏差变化趋势如何，都应该考虑控制器的输入应按最大（或最小）输出，以达到迅速调整偏差的效果，使偏差绝对值以最大的速度减小。

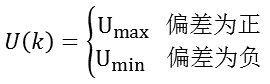
　　这种情况下其实相当于实施开环控制，是一种对偏差出现极限情况的快速响应。

（2）如果|e(k)|≤Mmax

　　这种情况我们需要更具系统的变化趋势来分析，具体的情况实施不同的控制方式，我们引入偏差增量来协助分析。

（2.1）当e(k)*∆e(k)>0或者∆e(k)=0时

　　这种情况说明偏差在朝向偏差绝对值增大的方向变化，或者偏差为某一固定值，此时我们再判断偏差的绝对值与偏差的中间值Mmid之间的关系。

（2.1.1）此时如果|e(k)|>Mmid，说明偏差也较大，可考虑由控制器实施较强的控制作用，以达到扭转偏差绝对值向减小的方向变化，并迅速减小偏差的绝对值。

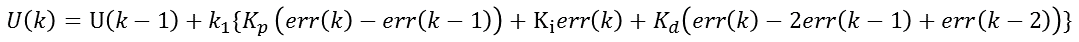
（2.1.2）此时如果|e(k)|≤Mmid，说明尽管偏差是向绝对值增大的方向变化，但是偏差绝对值本身并不是很大，可以考虑控制器实施一般的控制作用，只需要扭转偏差的变化趋势，使其向偏差绝对值减小的方向变化即可。

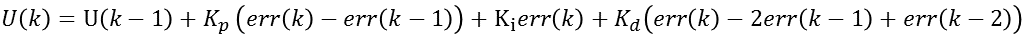
（2.2）当e(k)*∆e(k)<0且∆e(k)*∆e(k-1)>0或者e(k)=0时，说明偏差的绝对值向减小的方向变化，或者已经达到平衡状态，此时保持控制器输出不变即可。即：U(k)=U(k-1)。

（2.3）当e(k)*∆e(k)<0且∆e(k)*∆e(k-1)<0时，说明偏差处于极限状态。如果此时偏差的绝对值较大，|e(k)|>Mmid，可以考虑实施较强控制作用。

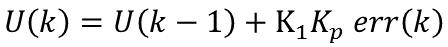
　　如果此时偏差绝对值较小，|e(k)|<Mmid，可以考虑实施较弱控制作用。

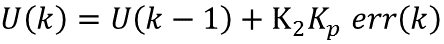
　　其中，k1为增益放大系数，k1取大于1的值；k2为增益抑制系数，取大于0而小于1的值。

（3）如果|e(k)|<Mmin

　　这种情况实际上说明偏差绝对值很小，这种偏差有可能是系统静差引起的，此时必须要引入积分作用，实施PID控制或者PI控制。

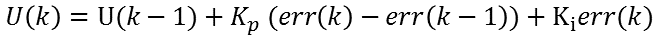
　　Kp和Ki可以适当减小，以减小控制作用。当偏差小到一定程度后，甚至可以引入死区的概念，是系统稳定下来而不需要去进行调节。

3、专家PID算法实现

　　前面我们了解了专家PID控制器的基本原理，并分析了一个较为常见的专家PID的控制规则。分析规则的过程其实也是一个推理的基本过程，所以我们得到了基本的规则库同时也有相应的推理机，接下来我们就来实现这一算法。

　　首先定义一个专家PID的结构体对象：

 /*定义结构体和公用体*/
 typedef struct
 {
   float setpoint;               /*设定值*/
   float kp;                     /*比例系数*/
   float ki;                     /*积分系数*/
   float kd;                     /*微分系数*/
   float lasterror;              /*前一拍偏差*/
   float preerror;               /*前两拍偏差*/
   float result;                 /*PID控制器结果*/
   float output;                 /*输出值，0-100，为百分比值*/
   float maximum;                /*输出值上限*/
   float minimum;                /*输出值下限*/
   float errorabsmax;            /*偏差绝对值最大值*/
   float errorabsmid;            /*偏差绝对值中位值*/
   float errorabsmin;            /*偏差绝对值最小值*/
 }EXPERTPID;

　　在上面分析的基础上我们很容易写出来一个专家PID的控制器如下：

 void ExpertPID(EXPERTPID vPID,float pv)
 {
   float thiserror;
   float deltaerror;
   float lastdeltaerror;
   float result;//本次调节输出值

   thiserror=vPID->setpoint-pv;
   deltaerror=thiserror-vPID->lasterror;
   lastdeltaerror=vPID->lasterror-vPID->preerror;

   if(abs(thiserror)>=vPID->errorabsmax)
   {/*执行规则1*/
     if(thiserror>)
     {
       result=vPID->maximum;
     }

     if(thiserror<)
     {
       result=vPID->minimum;
     }
   }

   if((thiserror*deltaerror>)||(deltaerror==))
   {/*执行规则2*/

     if(abs(thiserror)>=vPID->errorabsmid)
     {
       result=vPID->result+2.0*(vPID->kp*deltaerror+vPID->ki*thisError+vPID->kd*(deltaerror-lastdeltaerror);
     }
     else
     {
       result=vPID->result+0.4*(vPID->kp*deltaerror+vPID->ki*thisError+vPID->kd*(deltaerror-lastdeltaerror);
     }
   }

   if(((thiserror*deltaerror<)&&(deltaerror*lastdeltaerror>))||(thiserror==))
   {/*执行规则3*/
     result=vPID->result;
   }

   if((thiserror*deltaerror<)&&(deltaerror*lastdeltaerror<))
   {/*执行规则4*/
     if(abs(thiserror)>=vPID->errorabsmid)
     {
       result=vPID->result+2.0*output+vPID->kp*thiserror;
     }
     else
     {
       result=vPID->result+0.6*output+vPID->kp*thiserror;
     }
   }

   if((abs(thiserror)<=vPID->errorabsmin)&&(abs(thiserror)>))
   {/*执行规则5*/
     result=vPID->result+0.5*vPID->kp*deltaerror+0.3*vPID->ki*thiserror;
   }

   /*对输出限值，避免超调*/
   if(result>=vPID->maximum)
   {
     result=vPID->maximum;
   }

   if(result<=vPID->minimum)
   {
     result=vPID->minimum;
   }

   vPID->result=result;
   vPID->preerror=vPID->lasterror;
   vPID->lasterror=thiserror;
   vPID->output=(result/(vPID->maximum-vPID->minimum))*;
 }

4、专家PID总结

　　本节我们实现了一个专家PID控制器，这是一种专家规则直接与PID算法相结合的直接型专家控制器。通过分析PID的调节过程总结了5条规则，以这5条规则为基础实现了上述的算法。当然这只是一个普遍型的规则库，对于不同的被控对象和控制要求，我们可以采用不同的判断规则，而且各参数的选取需依赖于专家经验，所以规则的获取和使用也会有不同方式。

欢迎关注：