Verilog 加法器和减法器(8)-串行加法器
如果对速度要求不高,我们也可以使用串行加法器。下面通过状态机来实现串行加法器的功能。
设A=an-1an-2…a0, B=bn-1bn-2…b0,是要相加的两个无符号数,相加的和为:sum=sn-1sn-2…s0。我们现在要设计一个电路,在时钟周期内处理一位相加的串行加法。加法过程一开始进行a0,b0的相加,在下一个时钟周期完成 a1,b1和第0位进位的相加,并依次完成所有的加法。
下图的方案中,3个移位寄存器用来保存A,B以及和Sum。假设这些寄存器有并行加载功能,先将加A,B的值载入这些寄存器,在时钟的每个周期,通过加法器FSM控制每位相加,在周期的最后把输出的结果移入Sum寄存器。我们使用上升沿触发的触发器,这样所有数据在时钟的上升沿及各个触发器的传播延迟后发生变化,此时三个移位寄存器内容右移:将加法结果移入Sum,并将下一对 ai,bi加载至加法器FSM。
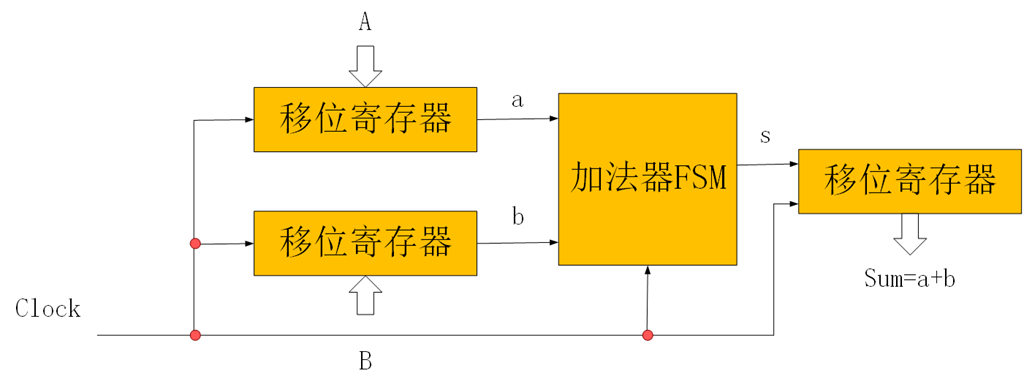
下面是加法器FSM的图:
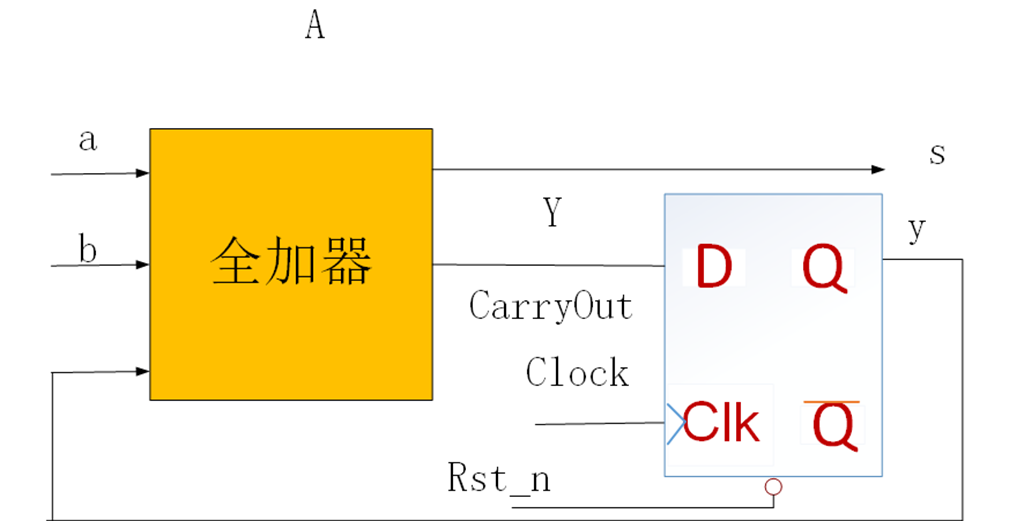
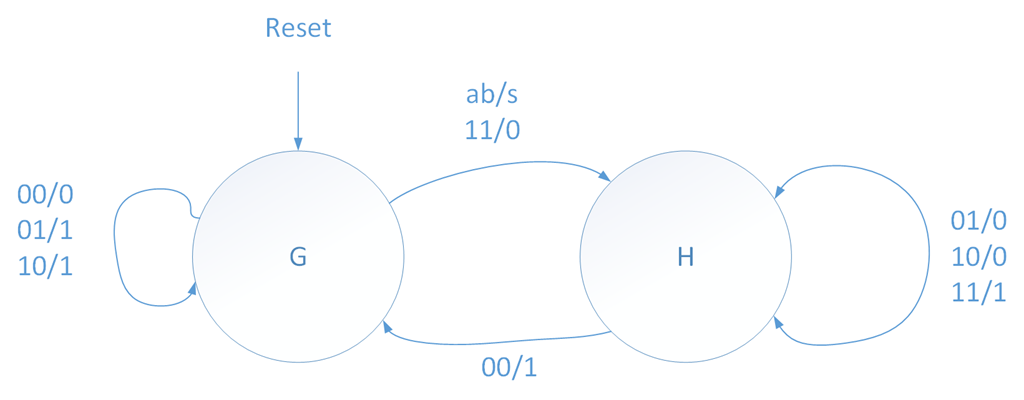
我们来设计状态机,假设有两个状态:状态G,进位为0,状态H,进位为1。则状态图如下,输出s取绝与当前状态(进位)和输入a,b的值,所以这是mealy型状态机。
在状态G中,输入00,则仍在状态G,输出为0,为01和10时候,仍在状态G,输出为1,如果输入为11,则转到状态H,输出0。
在状态H中,输入11,仍在状态H,输出1,输入为01和10时候,仍在状态H,输出为0,如果输入为00,则转到状态G,输出为1。
这个mealy型串行加法器的状态表如下:
根据状态表,利用卡诺图简化,有下列表达式,显然它就是全加器的输出表达式。
Y = ab+ay+by
s = a^b^y
| 现在状态 | 下一状态(ab) | 输出s | ||||||
| 00 | 01 | 10 | 11 | 00 | 01 | 10 | 11 | |
| G | G | G | G | H | 0 | 1 | 1 | 0 |
| H | G | H | G | G | 1 | 0 | 0 | 1 |
| 现在状态 | 下一状态(ab) | 输出(ab) | ||||||
| 00 | 01 | 11 | 10 | 00 | 01 | 11 | 10 | |
| y | Y | s | ||||||
| 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 |
下面是verilog实现代码,首先是移位寄存器的代码,该移位寄存器带有使能输入E,E=1时,寄存器的内容将在时钟的上升沿开始从左到右。E=0,可以阻止移位寄存器内容发生改变。
module shiftrne(R,L,E,w,clk,Q); parameter n=8;
input [n-1:0] R;
input L,E,w,clk;
output reg [n-1:0] Q; integer k; always @(posedge clk) begin
if(L)
Q<=R;
else if(E) begin
for(k=n-1; k>0; k=k-1)
Q[k-1] <= Q[k];
Q[n-1] <=w;
end end endmodule
下面是mealy型串行加法的代码,代码中首先例化了三个移位寄存器。代码中还包括一个递减计数器,用来完成n位加法并输出至移位寄存器后,停止加法器。
代码中我们采用高电平复位信号。输出端的使能信号为Run信号,只要Run信号为1,递减计数器每个时钟周期都会递减。
module serialadd(A,B,Rst,clk,S);
input [7:0] A,B;
input Rst,clk;
output wire [7:0] S; reg [3:0] Count;
reg s,y,Y;
wire [7:0] QA,QB;
wire Run;
parameter G=1'b0, H=1'b1; shiftrne #(.n(8)) shift_A(.R(A),.L(Rst),.E(1'b1),.w(1'b0),.clk(clk),.Q(QA));
shiftrne #(.n(8)) shift_B(.R(B),.L(Rst),.E(1'b1),.w(1'b0),.clk(clk),.Q(QB));
shiftrne #(.n(8)) shift_S(.R(8'b0),.L(Rst),.E(Run),.w(s),.clk(clk),.Q(S)); //adder FSM
//output and next state cominatioal circuit always @(QA,QB,y) begin case (y)
G:
begin
s = QA[0]^QB[0];
if(QA[0]&QB[0]) Y=H;
else Y=G; end
H:
begin
s = QA[0]~^QB[0];
if(~QA[0]&~QB[0]) Y=G;
else Y=H; end
default:
Y = G;
endcase
end //sequential block
always @(posedge clk)
if(Rst)
y<=G;
else
y<=Y; //control shift proecess
always @(posedge clk)
if(Rst) Count=8;
else if(Run) Count = Count-1; assign Run = |Count;
endmodule
testbench代码为:
`timescale 1ns/1ns
`define clock_period 20 module serialadd_tb;
reg clk;
reg Rst; reg [7:0] A,B;
wire [7:0] S; serialadd serialadd0(.A(A),.B(B),.Rst(Rst),.clk(clk),.S(S));
//serialadd_moore serialadd_moore0(.A(A),.B(B),.Rst(Rst),.clk(clk),.S(S));
always #(`clock_period/2) clk = ~clk; initial begin
clk=0;
A = 8'd35;
B = 8'd99;
Rst = 0;
#(`clock_period)
Rst = 1;
#(`clock_period)
Rst = 0; #(`clock_period*10) $stop; end endmodule
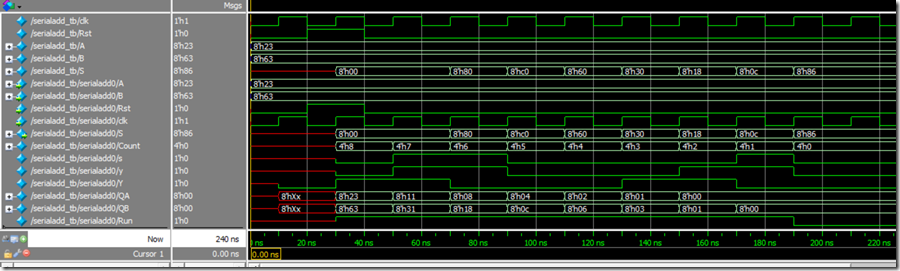
下面是mealy型串行加法的波形,输入35,99,输出134
我们把状态图做如下调整,拆分G为G0,G1,拆分H为H0,H1, 则输出之和状态有关,为moore型串行加法器状态图。
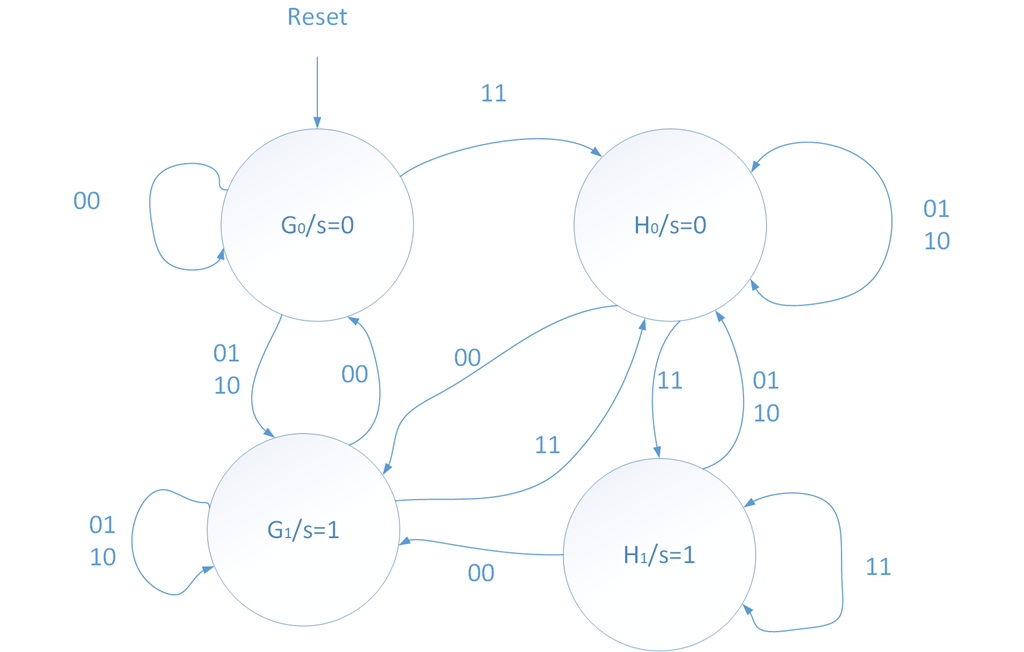
下面是该状态机的状态表:
| 现在状态 | 下一状态(ab) | 输出 | |||
| 00 | 01 | 10 | 11 | s | |
| G0 | G0 | G1 | G1 | H0 | 0 |
| G1 | G0 | G1 | G1 | H0 | 1 |
| H0 | G1 | H0 | H0 | H1 | 0 |
| H1 | G1 | H0 | H0 | H1 | 1 |
| 现在状态 | 下一状态(ab) | 输出 | |||
| 00 | 01 | 10 | 11 | s | |
| y2y1 | Y2Y1 | ||||
| 00 | 00 | 01 | 01 | 10 | 0 |
| 01 | 00 | 01 | 01 | 10 | 1 |
| 10 | 01 | 10 | 10 | 11 | 0 |
| 11 | 01 | 10 | 10 | 11 | 1 |
可以推导出
Y1=a^b^y2
Y2=ab+ay2+by2
s=y1
下面是其可能的实现电路。moore型加法输出比mealy型加法多了一个时钟周期的时延。
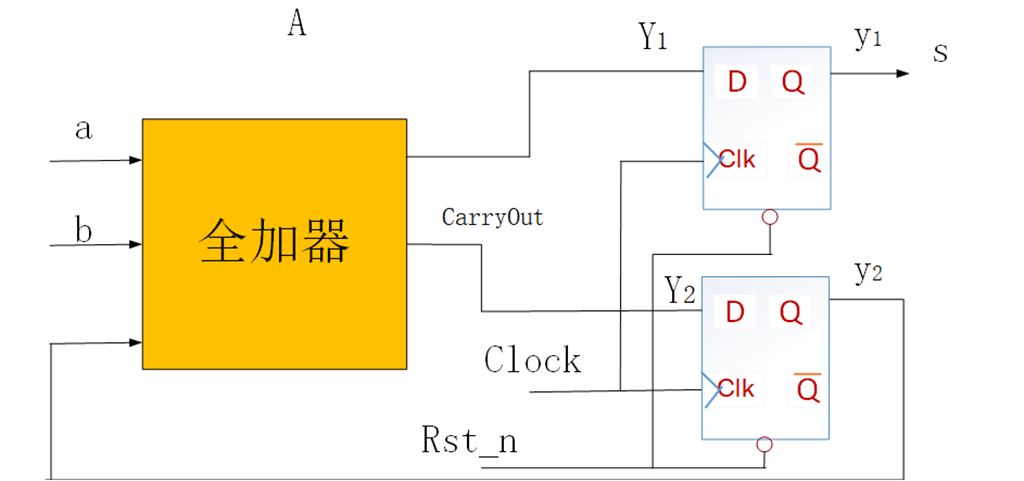
moore型串行加法器verilog代码如下,其中也例化了3个移位寄存器。注意Count复位后为9,
module serialadd_moore(A,B,Rst,clk,S);
input [7:0] A,B;
input Rst,clk;
output wire [7:0] S; reg [3:0] Count;
reg [1:0] y,Y;
wire [7:0] QA,QB;
wire s,Run;
parameter G0=2'b00, G1=2'b01,H0=2'b10, H1=2'b11; shiftrne #(.n(8)) shift_A(.R(A),.L(Rst),.E(1'b1),.w(1'b0),.clk(clk),.Q(QA));
shiftrne #(.n(8)) shift_B(.R(B),.L(Rst),.E(1'b1),.w(1'b0),.clk(clk),.Q(QB));
shiftrne #(.n(8)) shift_S(.R(8'b0),.L(Rst),.E(Run),.w(s),.clk(clk),.Q(S)); //adder FSM
//output and next state cominatioal circuit always @(QA,QB,y) begin case (y)
G0:
begin
if(QA[0]&QB[0]) Y=H0;
else if(~QA[0]&~QB[0]) Y=G0;
else Y=G1; end
G1:
begin
if(~QA[0]&~QB[0]) Y=G0;
else if (QA[0]&QB[0])Y=H0;
else Y=G1; end
H0:
begin
if(QA[0]&QB[0]) Y=H1;
else if(~QA[0]&~QB[0]) Y=G1;
else Y=H0; end
H1:
begin
if(~QA[0]&~QB[0]) Y=G1;
else if (QA[0]&QB[0])Y=H1;
else Y=H0; end
endcase
end //sequential block
always @(posedge clk)
if(Rst)
y<=G0;
else
y<=Y; //control shift proecess
always @(posedge clk)
if(Rst) Count=9;
else if(Run) Count = Count-1; assign Run = |Count;
assign s = (y==H0?1'b0:(y==G0?1'b0:1'b1));
endmodule
`timescale 1ns/1ns
`define clock_period 20 module serialadd_tb;
reg clk;
reg Rst; reg [7:0] A,B;
wire [7:0] S; //serialadd serialadd0(.A(A),.B(B),.Rst(Rst),.clk(clk),.S(S));
serialadd_moore serialadd_moore0(.A(A),.B(B),.Rst(Rst),.clk(clk),.S(S));
always #(`clock_period/2) clk = ~clk; initial begin
clk=0;
A = 8'd35;
B = 8'd99;
Rst = 0;
#(`clock_period)
Rst = 1;
#(`clock_period)
Rst = 0; #(`clock_period*10) $stop; end endmodule
输出波形为:
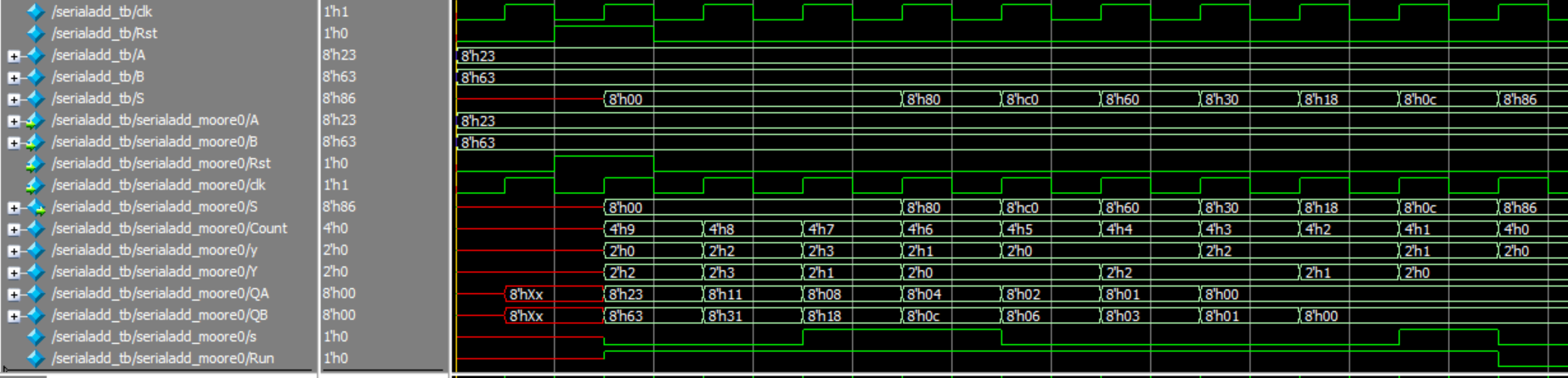
Verilog 加法器和减法器(8)-串行加法器的更多相关文章
- Verilog 加法器和减法器(4)
类似于行波进位加法器,用串联的方法也能够实现多位二进制数的减法操作. 比如下图是4位二进制减法逻辑电路图. 8位二进制减法的verilog代码如下: module subn(x, y, d,cin) ...
- Verilog 加法器和减法器(7)
在计算机中浮点数 表示通常采用IEEE754规定的格式,具体参考以下文章. https://www.cnblogs.com/mikewolf2002/p/10095995.html 下面我们在Veri ...
- Verilog 加法器和减法器(6)
为了减小行波进位加法器中进位传播延迟的影响,可以尝试在每一级中快速计算进位,如果能在较短时间完成计算,则可以提高加法器性能. 我们可以进行如下的推导: 设 gi=xi&yi, pi = xi ...
- Verilog 加法器和减法器(3)
手工加法运算时候,我们都是从最低位的数字开始,逐位相加,直到最高位.如果第i位产生进位,就把该位作为第i+1位输入.同样的,在逻辑电路中,我们可以把一位全加器串联起来,实现多位加法,比如下面的四位加法 ...
- Verilog 加法器和减法器(2)
类似半加器和全加器,也有半减器和全减器. 半减器只考虑当前两位二进制数相减,输出为差以及是否向高位借位,而全减器还要考虑当前位的低位是否曾有借位.它们的真值表如下: 对半减器,diff = x ^y, ...
- Verilog 加法器和减法器(1)
两个一位的二进制数x,y相加,假设和为s,进位为cout,其真值表为: 从真值表中,我们可以得到:s = x^y, cout = x&y,实现两个一位数相加的逻辑电路称为半加器. 实现该电路的 ...
- Verilog 加法器和减法器(5)
前面二进制加法运算,我们并没有提操作数是有符号数,还是无符号数.其实前面的二进制加法对于有符号数和无符号数都成立.比如前面的8位二进制加法运算,第一张图我们选radix是unsigned,表示无符号加 ...
- 基于Xilinx的Synthesize
所谓综合.就是讲HDL语言.原理图等设计输入翻译成由与.或.非们和RAM.触发器登记本逻辑单元的逻辑连接(即网表).并依据目标和要求(约束条件)优化生成的逻辑连接. ISE-XST XST是Xilin ...
- 乘法器——基于Wallace树的4位乘法器实现
博主最近在学习加法器乘法等等相关知识,在学习乘法器booth编码加Wallace树压缩时,发现在压缩部分积的时候用到了进位保留加法器(Carry Save Adder),博主对这种加法器不是很理解,而 ...
随机推荐
- Fiddler抓包8-打断点(bpu)
前言 先给大家讲一则小故事,在我们很小的时候是没有手机的,那时候跟女神聊天都靠小纸条.某屌丝A男对隔壁小王的隔壁女神C倾慕已久,于是天天小纸条骚扰,无奈中间隔着一个小王,这样小王就负责传小纸条了.有一 ...
- 内联外联CSS和JS
内联CSS 代码示例: <p style="color:red;font-size:18px">这里文字是红色.</p> 内联CSS也可称为行内CSS或者行 ...
- 集合List和ArrayList的示例
package chapter09; import java.util.ArrayList;import java.util.List; /* * List * ArrayList底层是数组 * 特点 ...
- 【C++ Primer | 15】C++类内存分布
C++类内存分布 书上类继承相关章节到这里就结束了,这里不妨说下C++内存分布结构,我们来看看编译器是怎么处理类成员内存分布的,特别是在继承.虚函数存在的情况下. 下面可以定义一个类,像下面这样: c ...
- 腾讯浏览服务X5内核集成
腾讯浏览服务X5内核集成https://www.jianshu.com/p/8a7224ff371a TBS 腾讯浏览器服务接入文档https://x5.tencent.com/tbs/guide/s ...
- java07接口与继承动手动脑
1.源代码: package Work; class A{ public A(){ System.out.println("Class A."); } public A(Strin ...
- 用户设置与virtual host配置
1.进入localhost:15672yemian 然后选择Admin菜单. 2.添加用户 caojun/123456 3.效果 4.virtual hosts添加 相当于db. /cjhost,一般 ...
- 006 Spark中的wordcount以及TopK的程序编写
1.启动 启动HDFS 启动spark的local模式./spark-shell 2.知识点 textFile: def textFile( path: String, minPartitions: ...
- 033 关于YARN的HA
一:准备 1.规划 namenode namenode ZKFC ZKFC journalnode journalnode jou ...
- Pathon1 - 基础1
一. Hello world程序 print("Hello World!") 执行命令: python hello.py ,输出 执行 python hello.py 时,明确的指 ...
