[LeetCode] 96. Unique Binary Search Trees(给定一个数字n，有多少个唯一二叉搜索树) ☆☆☆

[Leetcode] Unique binary search trees 唯一二叉搜索树

Unique Binary Search Trees leetcode java

描述

Given n, how many structurally unique BST's (binary search trees) that store values 1...n?

For example,
Given n = 3, there are a total of 5 unique BST's.

   1         3     3      2      1
    \       /     /      / \      \
     3     2     1      1   3      2
    /     /       \                 \
   2     1         2                 3

解析

递归

思路：空树和只有根节点时，也为BST。对于一点i，当其为根节点时，左子树的节点的个数为i-1，（为1,...i-1）,右子树的个数为n-i（为，i+1,...n）。对一个根来说，唯一二叉树的个数为左子树结点的个数乘以右子树的个数。而根节点可以从1到n 中选择。

可行的二叉查找树的数量，其实二叉查找树可以任意取根，只要满足中序遍历有序的要求就可以。从处理子问题的角度来看，选取一个结点为根，就把结点切成左右子树，以这个结点为根的可行二叉树数量就是左右子树可行二叉树数量的乘积，所以总的数量是将以所有结点为根的可行结果累加起来。

动态规划

这是Catalan Number卡特兰数的一个例子。卡特兰数的的递推公式：

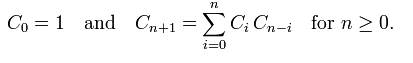
根据图示

以1为根的树有几个，完全取决于有二个元素的子树有几种。同理，2为根的子树取决于一个元素的子树有几个。以3为根的情况，则与1相同。

定义Count[i] 为以[0,i]能产生的Unique Binary Tree的数目，

如果数组为空，毫无疑问，只有一种BST，即空树，
    Count[0] =1

如果数组仅有一个元素{1}，只有一种BST，单个节点
    Count[1] = 1

如果数组有两个元素{1,2}， 那么有如下两种可能
    1                       2
     \                    /
       2                1
    Count[2] = Count[0] * Count[1]   (1为根的情况)
                  + Count[1] * Count[0]  (2为根的情况。

再看一遍三个元素的数组，可以发现BST的取值方式如下：
    Count[3] = Count[0]*Count[2]  (1为根的情况)
                  + Count[1]*Count[1]  (2为根的情况)
                  + Count[2]*Count[0]  (3为根的情况)

所以，由此观察，可以得出Count的递推公式为
    Count[i] = ∑ Count[0...k] * [ k+1....i]     0<=k<i-1
    问题至此划归为一维动态规划。

[Note]
    这是很有意思的一个题。刚拿到这题的时候，完全不知道从那下手，因为对于BST是否Unique，很难判断。最后引入了一个条件以后，立即就清晰了，即
    当数组为 1，2，3，4，.. i，.. n时，基于以下原则的BST建树具有唯一性：
   以i为根节点的树，其左子树由[1, i-1]构成， 其右子树由[i+1, n]构成。

维护量res[i]表示含有i个结点的二叉查找树的数量。

根据上述递推式依次求出1到n的的结果即可。

用一个数组保存 1 至 n-1 对应的不同二叉树的个数 X₁、X₂、X₃、... X_n-1，

则 n 对应的不同二叉树个数X_n = X_n-1 + X₁*X_n-2 + X₂*X_n-3 + X₃*X_n-4 + ... + X_n-2*X₁ + X_n-1

通过这个递推式，我们可以从 N = 1 开始递推，最后得到 N = n 时不同二叉查找树的个数。

时间上每次求解i个结点的二叉查找树数量的需要一个i步的循环，总体要求n次，所以总时间复杂度是O(1+2+...+n)=O(n^2)。空间上需要一个数组来维护，并且需要前i个的所有信息，所以是O(n)。

代码

递归

class Solution {
    public int numTrees(int n) {
        if (n == 0 || n == 1) {
            return 1;
        }
        int sum = 0;
        for(int i = 1; i <= n; ++i) {
            sum += numTrees(i - 1) * numTrees(n - i);
        }
        return sum;
    }
}

动态规划

class Solution {
    public int numTrees(int n) {
        if (n <= 0)
            return 0;
        int[] res = new int[n + 1];
        res[0] = 1;
        res[1] = 1;
        for (int i = 2; i <= n; i++) {
            for (int j = 0; j < i; j++) {
                res[i] += res[j] * res[i - j - 1];
            }
        }
        return res[n];
    }
}