【转】Unity四元数和向量相乘作用及其运算规则

作用：四元数和向量相乘表示这个向量按照这个四元数进行旋转之后得到的新的向量。

比如：向量vector3(0,0,10)，绕着Y轴旋转90度，得到新的向量是vector3(10,0,0)。

在unity中表示为：

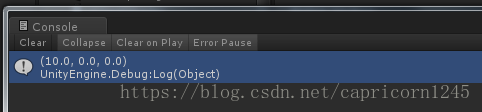
运行结果为：

复合旋转就是四元数依次相乘，最后乘以向量

多来几例：

想了解其中的运算过程的可以往下看。

将四元数的四个值分别计为：（w,x,y,z），unity中的四元数中的四个数字是（x,y,z,w），不影响下面的计算过程。

绕任意轴旋转任意角度的四元数为：

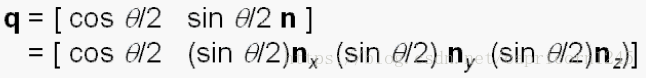
那么绕着Y轴旋转90度的四元数就是q = (√2/2 , 0 ， √2/2 ， 0)；

（unity中这个Quaternion.Euler(0,90,0)打debug的话是（0，√2/2 , 0 ， √2/2 ），因为排列顺序是（x,y,z,w），不影响下面的计算过程）

四元数乘以向量的运算规则为：q * v = （q） *（ v） *（ q−1）；

其中：

q = (√2/2 , 0 ， √2/2 ， 0)；

v，将v向量扩充为四元数（0，v）,也就是v = （0 , 0，0 , 10）；

q−1是四元数q的逆，求逆过程如下：

共轭四元数：q*=(w,-x,-y,-z)，也就是（√2/2 , 0 ， -√2/2 ， 0）
四元数的模：N(q) = √(x^2 + y^2 + z^2 +w^2)，即四元数到原点的距离，计算结果为1
四元数的逆：q−1=q*/N(q)，也就是q−1 = （√2/2 , 0 ， -√2/2 ， 0）
q * v = q * v * q−1 = (√2/2 , 0 ， √2/2 ， 0) * （0 , 0，0 , 10）*（√2/2 , 0 ， -√2/2 ， 0）；

四元数乘法公式：

按照上述计算公式： q * v = q * v * q−1

(√2/2 , 0 ， √2/2 ， 0) * （0 , 0，0 , 10） = （0,5√2，0，5√2）

（0,5√2，0，5√2） * （√2/2 , 0 ， -√2/2 ， 0）=（0,10,0,0）；

将最后得到的四元数（0,10,0,0）变为向量（0，newV），就是newV（10,0,0）。

---------------------
作者：capricorn1245
来源：CSDN
原文：https://blog.csdn.net/capricorn1245/article/details/82724830
版权声明：本文为博主原创文章，转载请附上博文链接！