2019 Multi-University Training Contest 7 Kejin Player(期望)

题意：给定在当前等级升级所需要的花费 每次升级可能会失败并且掉级 然后q次询问从l到r级花费的期望

思路：对于单次升级的期望 我们可以列出方程:

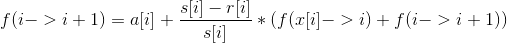
所以我们可以统计一下前缀和 每次询问O1回答

#include <bits/stdc++.h>
using namespace std;
const double pi = acos(-1.0);
const int N = 5e5+7;
const int inf = 0x3f3f3f3f;
const double eps = 1e-6;
typedef long long ll;
const ll mod = 1e9+7;
ll dp[N],r[N],s[N],x[N],a[N];
ll q_pow(ll a,ll n){
    ll ans=1; ll base=a;
    while(n){
        if(n&1) ans=(ans*base)%mod;
        base=base*base%mod;
        n>>=1;
    }
        return ans;
}
ll inv(ll a,ll b){
    return q_pow(a,b-2);
}
int main(){
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);
    int t;
    cin>>t;
    while(t--){
        int n,q; cin>>n>>q;
        for(int i=1;i<=n;i++){
            cin>>r[i]>>s[i]>>x[i]>>a[i];
        }
        for(int i=1;i<=n;i++){
            dp[i+1]=(s[i]*((dp[i]+a[i])%mod)%mod-(s[i]-r[i])%mod*dp[x[i]]%mod+mod)%mod*inv(r[i],mod)%mod;
        }
        for(int i=1;i<=q;i++){
            int l,r;
            cin>>l>>r;
            cout<<(dp[r]-dp[l]+mod)%mod<<endl;
        }
    }
}