[MIT6.006] 7. Counting Sort, Radix Sort, Lower Bounds for Sorting 基数排序，基数排序，排序下界

在前6节课讲的排序方法（冒泡排序，归并排序，选择排序，插入排序，快速排序，堆排序，二分搜索树排序和AVL排序）都是属于对比模型（Comparison Model）。对比模型的特点如下：

• 所有输入items是黑箱（ADTs, Abstract Data Types）；
• 允许的操作只有对比（<，≤，>，≥，=）；
• 时间消耗 = #对比。

之前绝大部分的对比模型是以决策树的结构出现的，这是因为任何对比模型都可以被认做所有可能对比、它们的结果和答案下的一棵树（原话：Decision Tree: any comparison algorithm can be viewed as a tree of all possible comparisons and their outcomes, and resulting answer.）

例如下图的二分查找树：

对比决策树结构和算法本身，它们各成分的对应情况如下：

问：查找最低下限是多大呢？

答：在n个预处理的items中, 用对比模型查找到指定的item，最坏情况下是Ω(log₂n)。因为对比模型为决策树且它为2分结构（binary），另外由上面举例的二分查找树也能发现叶子节点数一定是 ≥n 的，因此树的高度h ≥ log₂n。

问：排序最低下限是多大呢？

答：Ω(nlog₂n)，原因见下图：

扩展（资料来源：https://www.cnblogs.com/jin-nuo/p/5293554.html）：

就时间复杂度而言，排序分以下为四类：

排序分类	排序方法
平方阶O(n2)	直接插入、直接选择和冒泡排序
线性对数阶O(nlog2n)	快速排序、堆排序、归并排序，BST排序和AVL排序
O(n1+§),§是介于0和1之间的常数	希尔排序（还没讲到）
线性阶O(n)	基数排序

这节课的重点就是讲解线性阶时间复杂度的基数排序，在此之前，我们先了解下线性排序（Linear-time Sorting, integer sorting）:

• 假设n个键排序是整型，其属于{0, 1, ..., k-1}（每个跟一个word刚好合配，这里的word相当于一个内存地址似的概念）；
• 除了对比，可以做其他操作；
• 对于k，可以排序的时间复杂度为O(n)。

讲师讲了两个线性排序：计数排序（Counting Sort）和基数排序（Radix Sort）。

一、计数排序（Counting Sort）

个人感觉计数排序就是顺序字典计数 + 顺序输出。具体例子可以参考下：https://www.cnblogs.com/kyoner/p/10604781.html

二、计数排序（Radix Sort）

由于课程时间剩下不多，讲师没有详细展开这块内容，但要理解并不太难，首先，我引用博文https://blog.csdn.net/wolinxuebin/article/details/7488280的例子讲解下主要思路，基数排序的例子如下：

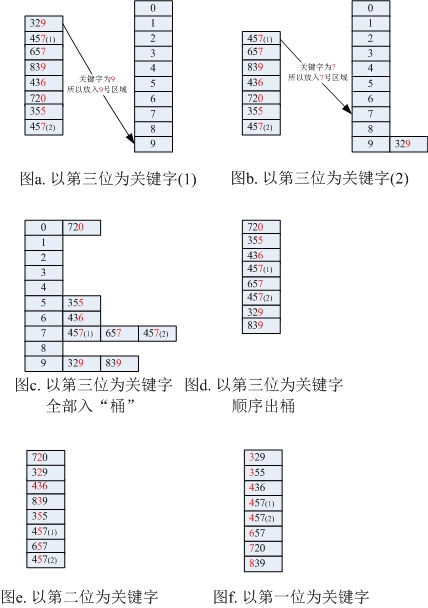
如果待排数组为[329, 457, 657, 839, 436, 720, 355, 457]，假设这里采用低位优先排序方式（Least significant digital, LSD）进行排序：

1. 由于待排数组中元素各位上的最大值不超过10, 那么这里建个10个桶[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]；
2. 以个位数字为桶编号依次入桶，全部入桶后再全部顺序出桶；
3. 以十位数字为桶编号依次入桶，全部入桶后再全部顺序出桶；
4. 以百位数字为桶编号依次入桶，全部入桶后再全部顺序出桶；
5. 完毕。

上面提到的低位优先排序方式LSD是以个位->十位->百位的顺序，而还有个高位优先排序方式（Most significant digital, MSD)是从百位->十位->个位。时间复杂度的计算：假设有n个d位数，每位数有k种（例如像上面的例子，每位数的范围是0-9，则k=10）则时间复杂度为Ο((n + k) x d) (注：n指分配n个数要n次，k指构建k个桶，d为低位/高位优先排序次数，即位数)。