Matrix Power Series(POJ 3233)

• 原题如下：
  Matrix Power Series

  Time Limit: 3000MS		Memory Limit: 131072K
  Total Submissions: 28044		Accepted: 11440

  Description

  Given a n × n matrix A and a positive integer k, find the sum S = A + A² + A³ + … + A^k.

  Input

  The input contains exactly one test case. The first line of input contains three positive integers n (n ≤ 30), k (k ≤ 10⁹) and m (m < 10⁴). Then follow n lines each containing n nonnegative integers below 32,768, giving A’s elements in row-major order.

  Output

  Output the elements of S modulo m in the same way as A is given.

  Sample Input

  2 2 4
  0 1
  1 1

  Sample Output

  1 2
  2 3

• 题解：构造矩阵：
  

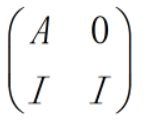
  此时，令S_k=I+A+…+A^k-1，则有：
  
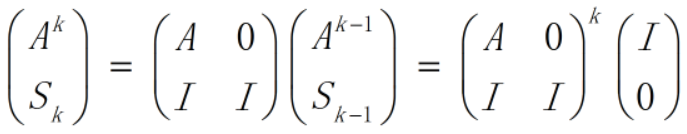
  通过计算这个矩阵的k次幂，就可求出A的累乘和，时间复杂度为O(n³logk)

• 代码：

   #include <cstdio>
   #include <cctype>
   #define number s-'0'
   #include <cstring>
   #include <vector>
  
   using namespace std;
  
   typedef vector<int> vec;
   typedef    vector<vec> mat;
  
   int n,k,m;
   mat A;
  
   void read(int &x)
   {
       char s;
       x=;
       bool flag=;
       while (!isdigit(s=getchar()))
           (s=='-')&&(flag=true);
       for (x=number; isdigit(s=getchar());x=x*+number);
       (flag)&&(x=-x);
   }
  
   void write(int x)
   {
       if (x<)
       {
           putchar('-');
           x=-x;
       }
       if (x>) write(x/);
       putchar(x%+'');
   }
  
   mat mul(mat &A, mat &B)
   {
       mat C(A.size(), vec(B[].size()));
       for (int i=; i<A.size(); i++)
       {
           for (int j=; j<B[].size(); j++)
           {
               for (int k=; k<B.size(); k++)
               {
                   C[i][j]=(C[i][j]+A[i][k]*B[k][j])%m;
               }
           }
       }
       return C;
   }
  
   mat pow(mat A, int n)
   {
       mat B(A.size(), vec(A.size()));
       for (int i=; i<A.size(); i++) B[i][i]=;
       while (n>)
       {
           if (n&) B=mul(B, A);
           A=mul(A, A);
           n>>=;
       }
       return B;
   }
  
   int main(int argc, char * argv[])
   {
       read(n);read(k);read(m);
       A=mat (n,vec(n));
       mat B(n*, vec(n*));
       for (int i=; i<n; i++)
       {
           for (int j=; j<n; j++)
           {
               read(A[i][j]);
               B[i][j]=A[i][j];
           }
           B[n+i][i]=B[n+i][n+i]=;
       }
       B=pow(B,k+);
       for (int i=; i<n; i++)
       {
           for (int j=; j<n; j++)
           {
               int a=B[n+i][j]%m;
               if (i==j) a=(a+m-)%m;
               printf("%d%c", a, j+==n?'\n':' ');
           }
       }
   }