20141016--for 兔子

             Console.Write("请输入月数：");
             int m =int.Parse(Console.ReadLine());
             int ct = ;//成兔对数ct
             int xt = ;//小兔对数xt
             int yt = ;//幼兔对数yt
             int zt = ;//总兔对数zt
             for (int i = ; i <= m; i++)
             {
                 if (i == )//定义第一个月的成兔幼兔小兔对数
                 {//（告诉电脑第一个月时兔子对数）
                     ct = ;//第一个月成兔对数=0
                     xt = ;//第一个月小兔对数=0
                     yt = ;//第一个月幼兔对数=1
                 }
                 else
                 {
                     ct = xt + ct;//每月成兔对数等于上月小兔对数+上月成兔对数
                     xt = yt;//每月小兔对数等于上月幼兔对数
                     yt = ct;//每月幼兔对数等于本月的成兔对数
                 }
                  zt = ct + xt + yt;//总兔对数等于成兔加小兔加幼兔
                 Console.WriteLine(i.ToString() + "个月后成兔对数是：" + ct.ToString());
                 Console.WriteLine(i.ToString() + "个月后小兔对数是：" + xt.ToString());
                 Console.WriteLine(i.ToString() + "个月后幼兔对数是：" + yt.ToString());
                 Console.WriteLine(i.ToString() + "个月后兔子总对数是：" + zt.ToString());
                 Console.ReadLine();
             }
             Console.ReadLine();  

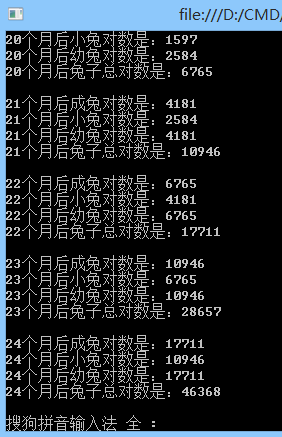
有成兔3对，小兔2对，幼兔5对，3个月后幼兔成长成小兔，小兔成长成成兔，每对成兔生下一对幼兔，

             Console.Write("请输入月数");
             int m =int.Parse(Console.ReadLine());
             int ct = ;//成兔对数ct
             int xt = ;//小兔对数xt
             int yt = ;//幼兔对数yt
             int zt = ;//总兔对数zt
             for (int i = ; i <= m; i = i + )
             {
                 if ( i == )
                 {
                     ct = ;//第一个月成兔对数
                     xt = ;//第一个月小兔对数
                     yt = ;//第一个月幼兔对数
                     zt = ct + yt + xt;//第一个月总兔对数
                 }
                 else
                 {
                     ct = ct + xt;//本月成兔对数=上月成兔对数+上月小兔对数
                     xt = yt;//本月小兔对数=上月幼兔对数
                     yt = ct;//本月幼兔对数=本月成兔对数
                 }
                 zt = ct + xt + yt;//总兔对数等于成兔加小兔加幼兔
                 Console.WriteLine("第" + (i).ToString() + "个月时成兔对数是：" + ct.ToString());
                 Console.WriteLine("第" + (i).ToString() + "个月时小兔对数是：" + xt.ToString());
                 Console.WriteLine("第" + (i).ToString() + "个月时幼兔对数是：" + yt.ToString());
                 Console.WriteLine("第" + (i).ToString() + "个月时兔子总对数是：" + zt.ToString());
                 Console.ReadLine();
             }