测来测去，感觉REQUESTS最实在

URLLIB,URLLIB2,PYCURL,HTTPIE,，，在测试PUT及认证时，还是REQUESTS胜出。。

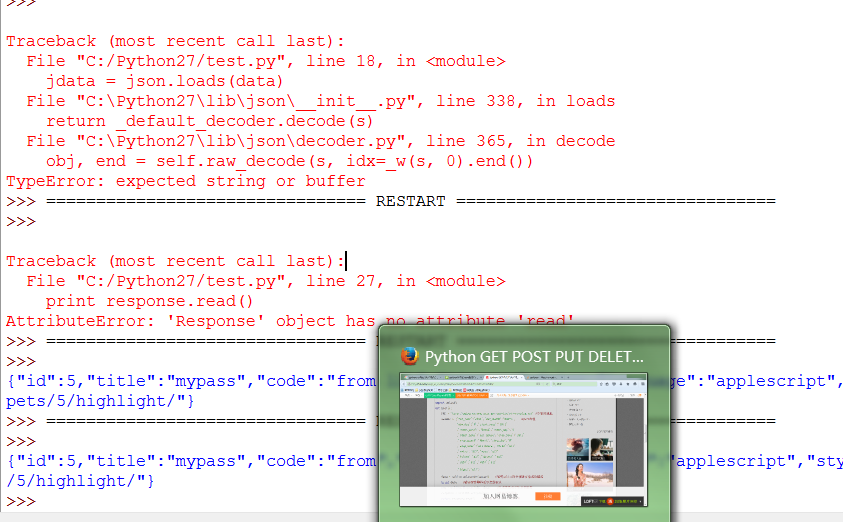
测试过程及样例代码如下：

import urllib
import urllib2
import base64
import json
import requests

#GET
url = 'http://127.0.0.1:8000/snippets/'
request = urllib2.Request(url)
base64string = base64.encodestring('%s:%s' % ('admin', 'admin')).replace('\n', '')
request.add_header("Authorization", "Basic %s" % base64string)
request.get_method = lambda: 'GET'
response = urllib2.urlopen(request)
print response.read()

#PUT

url = 'http://127.0.0.1:8000/snippets/5/'
data = {'code':'from', 'title':'mypass'}
response = requests.put(url, data=data, auth=('admin','admin'))
#request = urllib2.Request(url, data=jdata, auth=('admin','admin'))
#base64string = base64.encodestring('%s:%s' % ('admin', 'admin')).replace('\n', '')
#request.add_header("Authorization", "Basic %s" % base64string)
#request.get_method = lambda: 'PUT'
#opener = urllib2.build_opener(urllib2.HTTPHandler)
#response = opener.open(request)  

print response.text

#POST
url = 'http://127.0.0.1:8000/snippets/'
data = {'code':'from lib', 'title':'mypass'}
request = urllib2.Request(url)
data = urllib.urlencode(data)
base64string = base64.encodestring('%s:%s' % ('admin', 'admin')).replace('\n', '')
request.add_header("Authorization", "Basic %s" % base64string)
opener = urllib2.build_opener()
response = opener.open(request, data)
print response.read()

#DELETE
url = 'http://127.0.0.1:8000/snippets/4/'
request = urllib2.Request(url)
base64string = base64.encodestring('%s:%s' % ('admin', 'admin')).replace('\n', '')
request.add_header("Authorization", "Basic %s" % base64string)
request.get_method = lambda: 'DELETE'
response = urllib2.urlopen(request)

print response.read()