排序算法<No.7>【希尔排序】

排序算法进入到第7篇，这个也还是比较基础的一种，希尔排序，该排序算法，是依据该算法的发明人donald shell的名字命名的。1959年，shell基于传统的直接插入排序算法，对其性能做了下提升，其思路，主要是基于下面的原因进行的：

1. 插入排序在对几乎已经排好序的数据操作时，效率高，即可以达到线性排序的效率。
2. 但插入排序一般来说是低效的，因为插入排序每次只能将数据移动一位。

下面，我们就看看希尔排序，具体的实现思路如下：

希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止

由上面的分析可知，希尔排序，其实是对原始待排序列的分组插入排序，这种分组，很巧妙，再次体现了分而治之这个思想的厉害。前面介绍过的排序：

排序算法<No.3>【桶排序】，排序算法<No.4>【基数排序】都是分治思想的体现。

针对上面的实现思路，可以将其分解为如下的代码实现步骤：

1. 获取原始待排记录的元素个数len，并计算初始增量d=len/2

2. 通过d = d/2进行循环，对待排记录进行分组，d作为增量值，每间隔d的元素被划分到一组

3. 对2中每组元素进行直接插入排序算法进行排序

4. 重复2,3的过程，直到2中计算的增量d=1的这轮排序结束，程序退出，排序完成

下面，举个栗子来看看，希尔排序的实现过程吧，例如待排序列：59，48，75，107，86，23，37，59，65，14

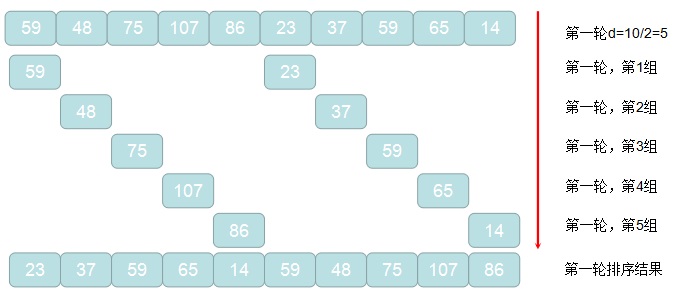
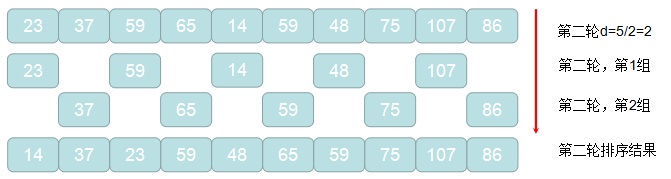
相应的java代码实现如下：

/**
 * @author "shihuc"
 * @date   2017年4月9日
 */
package shellSort;

import java.io.File;
import java.io.FileNotFoundException;
import java.util.Scanner;

/**
 * @author "shihuc"
 *
 */
public class Solution {

    /**
     * @param args
     */
    public static void main(String[] args) {
        File file = new File("./src/shellSort/sample.txt");
        Scanner sc = null;
        try {
            sc = new Scanner(file);
            int N = sc.nextInt();
            for (int i = ; i < N; i++) {
                int S = sc.nextInt();
                int A[] = new int[S];
                for (int j = ; j < S; j++) {
                    A[j] = sc.nextInt();
                }
                shellSort(A);
                print(A, i, "....");
            }
        } catch (FileNotFoundException e) {
            e.printStackTrace();
        } finally {
            if (sc != null) {
                sc.close();
            }
        }

    }

    /**
     * 希尔排序的实现过程
     *
     * @param src 待排序的原始数列
     */
    private static void shellSort(int src[]) {

        /*
         * 实现步骤 （1）
         * 获取原始待排记录的元素个数len，并计算初始增量d=len/2
         */
        int d = src.length / ;

        /*
         * 实现步骤（4）
         */
        while (d > ) {

            /*
             * 实现步骤（3）
             * 通过增量d对待排序的数列进行分组，进行插入排序. 注意，排序中待比较的元素之间的差距是d
             */
            for(int i = d; i<src.length; i=i+d){

                int temp = src[i];
                int j = i - d;

                /*
                 * 在获取参考值，也就待排序数列中当前位置的值，然后与其前面的需要排序的组内成员进行
                 * 插入排序。注意，这里的步长是d，和直接插入排序算法中的步长1的差异。认真想想，不难理解的。
                 */
                while(j >= && src[j] > temp){
                    src[j+d] = src[j];
                    j = j - d;
                }
                src[j+d] = temp;
            }

            /*
             * 实现步骤（2）
             * 下面这个过程，其实就是不断迭代计算出新的增量d。
             */
            d = d / ;
        }
    }

    /**
     * 用来打印输出堆中的数据内容。
     *
     * @param A
     *            堆对应的数组
     * @param idx
     *            当前是第几组待测试的数据
     * @param info
     *            打印中输出的特殊信息
     */
    private static void print(int A[], int idx, String info) {
        System.out.println(String.format("No. %02d %s ====================== ", idx, info));
        for (int i = ; i < A.length; i++) {
            System.out.print(A[i] + ", ");
        }
        System.out.println();
    }
}

测试栗子文件内容如下：

测试运行的结果如下：

No.  .... ======================
, , , , , , , , , ,
No.  .... ======================
, , , , , , ,
No.  .... ======================
, , , , , , , , , ,
No.  .... ======================
, , , , , , , , , , ,
No.  .... ======================
, , , , , , ,
No.  .... ======================
, , , , , , , , , 

其实，还是比较简单的，重点在于分组，插入排序的步长由原来的普通插入排序步长1变成了现在的d。