lua --- Module

首先需要明白，一般情况下，我们的定义的lua模块的文件与模块名(其实就是table的名字)是一致的，当然，不一致代码也是可以编译的(亲测)，之所以这样，本人认为是为了实际项目中管理的方便。以下是定义模块的集中方式(文件名字是 GameMudle.lua):

方式一：

 GameModule = {};

 function GameModule.ShowName()
     print("fun : ShowName");
 end

 function GameModule.ShowInfo()
     print("fun : ShowInfo");
 end

 return GameModule;

假如有一天，我们想要修改模块的名字了,就需要逐行代码的去修改对应的模块名字，显然，这实际非常不合理的。

以下是调整过的一种定义方式:

 GameModule = {};

 local this = GameModule;

 function this..ShowName()
     print("fun : ShowName");
 end

 function this.ShowInfo()
     print("fun : ShowInfo");
 end

 return this;

这样的话，每次修改模块的名字，我们只需要去修改第一行和第三行就可以了。但是还有一个问题，就是开始提到的，为了工程管理的方便，模块所在的lua文件名字与模块名需要保持一致，这样的话，我们没次更改模块名字，

需要同时修改模块名和模块所在的lua文件名，思考一下还有更好的定义模块的方式吗？显然是有的(哈哈哈。。。)。

以下是另外一种定义模块的方式:

 local this = {};

 local moduleName = ...;   --传递模块名，可以理解为文件名
 _G[moduleName] = this;    --将全局环境设置为 this   

 function this.ShowName()
     print("fun : ShowName");
 end

 function this.ShowInfo()
     print("fun : ShowInfo");
 end

 return this;

进一步简化：

 local this = {};

 local moduleName = ...;               --传递模块名，可以理解为文件名
 _G[moduleName] = this;                --将全局环境设置为 this，环境其实可以理解为一个表
 setmetatable(this,{__index = _G})      --没有这一句，全局的 print 等内置函数将不能使用
 setfenv(, this)                      --创建一个非全局环境 ，防止在全局环境中方法等命名的冲突,这里改变的是运行环境

 --全局环境设置为 this ，于是，我们直接定义函数的时候，不需要再带 this 前缀。
 --因为此时的全局环境就是M，不带前缀去定义变量，就是全局变量，这时的全局变量是保存在 this 里。
 function ShowName()
     print("fun : ShowName");
 end

 function ShowInfo()
     print("fun : ShowInfo");
 end

利用 module 函数进一步简化模块的定义:

 module(..., package.seeall);
 function ShowName()
     print("fun : ShowName");
 end

 function ShowInfo()
     print("fun : ShowInfo");
 end

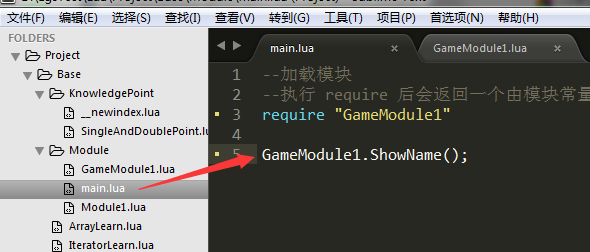
调用方式: