Problem 5 素数筛法+并查集

$des$

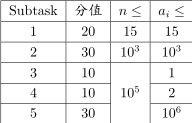
给定一个长度为 $n$ 的正整数序列 ${a_i }$。
将 ${1,2,...,n}$ 划分成两个非空集合 $S、T$，使得 $gcd(\prod_{i \in S} a_i,

\prod_{i \in T} a_i) = 1$
求划分方案数，对 $10^9 + 7$ 取模。

$sol$

对于两个数 $a, b$ 必须处于同一个集合，当其含有相同因子。
这样的话，将含有相同因子的数用并查集维护。
最后统计所有的 $n$ 个数被分成了 $x$ 个集合
答案就是 $2 ^ n - 2$，$1$ 需要特判

#include <bits/stdc++.h>

using namespace std;

#define gc getchar()
inline int read() {
    int x = ; char c = gc;
    while(c < '' || c > '') c = gc;
    while(c >= '' && c <= '') x = x *  + c - '', c = gc;
    return x;
}

#define Rep(i, a, b) for(int i = a; i <= b; i ++)
#define LL long long

const int N = 1e5 + , To = 1e6;

bool Check[To + ];
int tot, prime[To];

int fa[To + ];
int n;
int A[N];
bool Use[To];

void Get() {
    Rep(i, , To) {
        if(!Check[i]) prime[++ tot] = i;
        Rep(j, , tot) {
            if(prime[j] * i > To) break;
            Check[i * prime[j]] = ;
            if(i % prime[j] == ) break;
        }
    }
}

int Get(int x) {
    return fa[x] == x ? x : fa[x] = Get(fa[x]);
}

const int Mod = 1e9 + ;

LL Ksm(LL a, LL b) {
    LL ret = ;
    while(b) {
        if(b & ) ret = ret * a % Mod;
        a = a * a % Mod;
        b >>= ;
    }
    return ret;
}

int vis[To];

int main() {
    Get();
    for(int T = read(); T; T --) {
        n = read();
        int js = ;
        memset(Use, , sizeof Use);
        int Max = ;
        Rep(i, , n) A[i] = read(), Use[A[i]] = , Max = max(Max, A[i]), js += (A[i] == );
        Rep(i, , To) fa[i] = i;
        Rep(i, , tot) {
            if(prime[i] > Max) break;
            for(int j = ; j * prime[i] <= Max; j ++) {
                int num = j * prime[i];
                if(Use[num]) {
                    int fa1 = Get(num), fa2 = Get(prime[i]);
                    if(fa1 != fa2) fa[fa1] = fa2;
                }
            }
        }
        LL up = ;
        Rep(i, , n) {
            int f = Get(A[i]);
            if(vis[f] != T) vis[f] = T, up ++;
        }
        if(js > ) up += (js - );
        LL ans = Ksm(, up);
        ans -= ;
        if(ans < ) ans += Mod;
        cout << ans << "\n";
    }

    return ;
}