JavaScript图形实例:图形的扇形变换和环形变换
1.1 扇形变换
将如图1所示的上边长方形的图形变换为下边的扇形图形的变换称为扇形变换。
设长方形图形中任一点P1(X1,Y1)变换为扇形图形上的点P2(X2,Y2),长方形的长为X,扇形圆心坐标为(X0,Y0),扇形半径为L,扇形与X轴的最小夹角为B,扇形弧对应夹角为C,则点P2的坐标计算公式为:
X2=(L+Y1)*COS(θ)+X0
Y2=-(L+Y1)*SIN(θ)+Y0
其中: θ=C*(X-X1)/X1+B
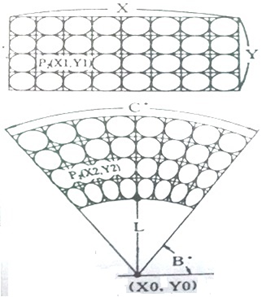
图1 扇形变换
生成一个六瓣花型图案的基本数据,将长方形中的8个六瓣花型作为基本图案,进行指定层数的扇形变换。
编写如下的HTML代码。
<!DOCTYPE html>
<head>
<title>扇形变换</title>
<script type="text/javascript">
function drawBase(id)
{
var canvas=document.getElementById(id);
if (canvas==null)
return false;
var context=canvas.getContext('2d');
context.fillStyle="#EEEEFF";
context.fillRect(0,0,700,100);
context.fillStyle="yellow";
context.strokeStyle="red";
context.lineWidth=2;
context.beginPath();
var dig=Math.PI/64;
var x=new Array();
var y=new Array();
var w=80;
// 生成一个六瓣花型图案的数据
for (var i=0;i<=128;i++)
{
d=w/2*(0.8+Math.sin(18*i*dig)/5)*1.2;
t=d*(0.5+Math.sin(6*i*dig)/2);
x[i]=t*Math.cos(i*dig);
y[i]=t*Math.sin(i*dig);
}
// 在水平一行中绘制8个六瓣花型图案
for (n=1;n<=8;n++)
{
px=(2*n-1)/2*w+30;
for (i=0;i<=128;i++)
{
x1=px+x[i];
y1=w/2-y[i];
if (i==0)
{
context.moveTo(x1,y1);
bx=x1; by=y1;
}
else
context.lineTo(x1,y1);
}
}
context.lineTo(bx,by);
context.closePath();
context.stroke();
context.fill();
}
function drawSector(id)
{
var canvas=document.getElementById(id);
if (canvas==null)
return false;
var context=canvas.getContext('2d');
context.fillStyle="#EEEEFF";
context.fillRect(0,0,700,500);
context.fillStyle="yellow";
context.strokeStyle="red";
context.lineWidth=2;
context.beginPath();
var dig=Math.PI/64;
w=80;
var x=new Array();
var y=new Array();
// 生成一个六瓣花型图案的数据
for (var i=0;i<=128;i++)
{
d=w/2*(0.8+Math.sin(18*i*dig)/5)*1.2;
t=d*(0.5+Math.sin(6*i*dig)/2);
x[i]=t*Math.cos(i*dig);
y[i]=t*Math.sin(i*dig);
}
var k=eval(document.myForm.levelNum.value);
if (k<1 || k>=6) {
alert("扇形层数需设定为1~5之一!");
return;
}
// 进行多重扇形变换
l=100; b=Math.PI/3; c=Math.PI/3; x0=350; y0=500;
for (m=1;m<=k;m++)
for (n=1;n<=8;n++)
for (var i=0;i<=128;i++)
{
px=(2*n-1)/2*w;
py=(2*m-1)/2*w;
x1=px+x[i];
y1=py-y[i];
th=c*(w*8-x1)/(w*8)+b;
x2=(l+y1)*Math.cos(th)+x0;
y2=-(l+y1)*Math.sin(th)+y0;
if (i==0)
{
context.moveTo(x2,y2);
bx=x2; by=y2;
}
else
context.lineTo(x2,y2);
}
context.lineTo(bx,by);
context.closePath();
context.stroke();
context.fill();
}
</script>
</head>
<body onload="drawBase('myCanvas1');">
基本图案<br/>
<canvas id="myCanvas1" width="700" height="100">您的浏览器不支持canvas!</canvas>
<form name="myForm">
扇形中基本图案层次数<input type=number name="levelNum" value=4 size=3>
<input type=button value="确定" onClick="drawSector('myCanvas2');">
</form><br>
<canvas id="myCanvas2" width="700" height="500">您的浏览器不支持canvas!</canvas>
</body>
</html>
将上述HTML代码保存到一个html文本文件中,再在浏览器中打开包含这段HTML代码的html文件,在“扇形中基本图案层次数”数值框中输入“5”,单击“确定”按钮,可以在浏览器窗口中看到基本六瓣花型图案的5层扇形变换,如图2所示。
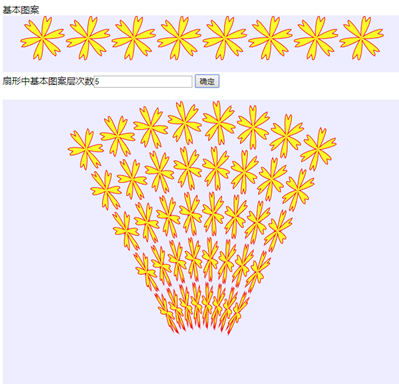
图2 扇形变换
1.2 环形变换
将如图3所示的上边长方形带状图形变换为下边的环状图形的变换称为环形变换。环状变换将带状图的左右两端接在一起,因而带状图的上部被拉伸,下部被压缩。
设带状图形中任一点P1(X1,Y1)变换为环状图形上的点P2(X2,Y2),带状长方形的长为X,环状图形的圆心坐标为(PX,PY),L为环形内半径(L的值越小,变换后图案的变形越大),则点P2的坐标计算公式为:
X2=(L+Y1)*COS(θ)+PX
Y2=-(L+Y1)*SIN(θ)+PY
其中: θ=2π*(X-X1)/X
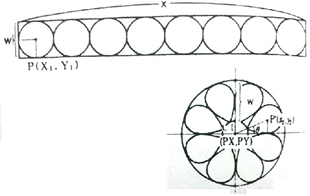
图3 环形变换
按环形变换的方法将如图4所示的基本图案进行环形变换。

图4 用于环形变换的基本图案
编写如下的HTML代码。
<!DOCTYPE html>
<head>
<title>环形变换</title>
<script type="text/javascript">
function draw1(id)
{
var canvas=document.getElementById(id);
if (canvas==null)
return false;
var context=canvas.getContext('2d');
context.fillStyle="#EEEEFF";
context.fillRect(0,0,800,500);
context.fillStyle="yellow";
context.strokeStyle="red";
context.lineWidth=1;
context.beginPath();
var dig=Math.PI/64;
var x=new Array();
var y=new Array();
var w=100;
// 生成一个六瓣花型图案的数据
for (var i=0;i<=128;i++)
{
d=w/2*(0.8+Math.sin(18*i*dig)/5)*1.2;
t=d*(0.5+Math.sin(6*i*dig)/2);
x[i]=t*Math.cos(i*dig);
y[i]=t*Math.sin(i*dig);
}
// 在水平一行中绘制8个六瓣花型图案
for (n=1;n<=8;n++)
{
px=(2*n-1)/2*w;
for (i=0;i<=128;i++)
{
x1=px+x[i];
y1=w/2-y[i];
if (i==0)
{
context.moveTo(x1,y1);
bx=x1; by=y1;
}
else
context.lineTo(x1,y1);
}
}
context.lineTo(bx,by);
context.closePath();
context.stroke();
context.fill();
}
function draw2(id)
{
var canvas=document.getElementById(id);
if (canvas==null)
return false;
var context=canvas.getContext('2d');
context.fillStyle="#EEEEFF";
context.fillRect(0,0,800,500);
context.fillStyle="yellow";
context.strokeStyle="red";
context.lineWidth=2;
context.beginPath();
var dig=Math.PI/64;
var x=new Array();
var y=new Array();
var w=100;
var l=80;
// 生成一个六瓣花型图案的数据
for (var i=0;i<=128;i++)
{
d=w/2*(0.8+Math.sin(18*i*dig)/5)*1.2;
t=d*(0.5+Math.sin(6*i*dig)/2);
x[i]=t*Math.cos(i*dig);
y[i]=t*Math.sin(i*dig);
}
// 进行一重环形变换
for (n=1;n<=8;n++)
for (var i=0;i<=128;i++)
{
px=(2*n-1)/2*w;
x1=px+x[i];
y1=w/2+y[i];
th=2*Math.PI*(w*8-x1)/(w*8);
x2=(l+y1)*Math.cos(th)+400;
y2=(l+y1)*Math.sin(th)+250;
if (i==0)
{
context.moveTo(x2,y2);
bx=x2; by=y2;
}
else
context.lineTo(x2,y2);
}
context.lineTo(bx,by);
context.closePath();
context.stroke();
context.fill();
}
function draw3(id,k)
{
var canvas=document.getElementById(id);
if (canvas==null)
return false;
var context=canvas.getContext('2d');
context.fillStyle="#EEEEFF";
context.fillRect(0,0,800,500);
context.fillStyle="yellow";
context.strokeStyle="red";
context.lineWidth=2;
context.beginPath();
var dig=Math.PI/64;
w=200/k; l=0;
var x=new Array();
var y=new Array();
// 生成一个六瓣花型图案的数据
for (var i=0;i<=128;i++)
{
d=w/2*(0.8+Math.sin(18*i*dig)/5)*1.2;
t=d*(0.5+Math.sin(6*i*dig)/2);
x[i]=t*Math.cos(i*dig);
y[i]=t*Math.sin(i*dig);
}
// 进行多重环形变换
for (m=1;m<=k;m++)
for (n=1;n<=8;n++)
for (var i=0;i<=128;i++)
{
px=(2*n-1)/2*w;
py=(2*m-1)/2*w;
x1=px+x[i];
y1=py-y[i];
th=2*Math.PI*(w*8-x1)/(w*8);
x2=(l+y1)*Math.cos(th)+400;
y2=(l+y1)*Math.sin(th)+250;
if (i==0)
{
context.moveTo(x2,y2);
bx=x2; by=y2;
}
else
context.lineTo(x2,y2);
}
context.lineTo(bx,by);
context.closePath();
context.stroke();
context.fill();
}
</script>
</head>
<body>
<button onClick="draw1('myCanvas');">基本图案</button>
<button onClick="draw2('myCanvas');">环形变换</button>
<button onClick="draw3('myCanvas',2);">二重环形变换</button>
<button onClick="draw3('myCanvas',3);">三重环形变换</button>
<br/><br/>
<canvas id="myCanvas" width="800" height="500">您的浏览器不支持canvas!</canvas>
</body>
</html>
将上述HTML代码保存到一个html文本文件中,再在浏览器中打开包含这段HTML代码的html文件,可以看到在浏览器窗口中,出现“基本图案”、“环形变换”、“二重环形变换”、“三重环形变换”这四个按钮,单击“基本图案”按钮,绘制出如图4所示的基本图案,单击“环形变换”,绘制出如图5所示的环形变换图案,单击“二重环形变换”,绘制出如图6所示的二重环形变换图案,单击“三重环形变换”,绘制出如图7所示的三重环形变换图案。

图5 环形变换图案

图6 二重环形变换图案

图7 三重环形变换图案
下面我们将上面的例子进行扩充,提供多种基本图案的选择,选择好基本图案后,进行环形变换。编写的HTML文件内容如下。
<!DOCTYPE html>
<head>
<title>可选择图案的环形变换</title>
<script type="text/javascript">
// 定义保存基本图案数据的二维数组
var x=new Array(10);
var y=new Array(10);
for (var i=0;i<10;i++)
{
x[i]=new Array(129);
y[i]=new Array(129);
}
var sele=0;
function initGraph()
{
var dig=Math.PI/64;
var w=100;
// 生成一个六瓣花型图案的数据
for (var i=0;i<=128;i++)
{
d=10*Math.sin(8*(i*dig+Math.PI/16));
x[0][i]=d*Math.cos(i*dig)+30*Math.cos(i*dig)*Math.cos(i*dig)*Math.cos(i*dig);
y[0][i]=d*Math.sin(i*dig)+30*Math.sin(i*dig)*Math.sin(i*dig)*Math.sin(i*dig);
}
// 生成一个六瓣花型图案的数据
for (var i=0;i<=128;i++)
{
d=w/2*(0.8+Math.sin(18*i*dig)/5)*1.2;
t=d*(0.5+Math.sin(6*i*dig)/2);
x[1][i]=t*Math.cos(i*dig);
y[1][i]=t*Math.sin(i*dig);
}
// 生成一个六瓣花型图案的数据
for (var i=0;i<=128;i++)
{
d=35*Math.sqrt(Math.abs(Math.cos(3*i*dig)));
t=d+10*Math.sqrt(Math.abs(Math.cos(9*i*dig)));
x[2][i]=t*Math.cos(i*dig)*1.2;
y[2][i]=t*Math.sin(i*dig);
}
}
initGraph();
function seleShape()
{
sele=document.frm.shape.selectedIndex-1;
drawBase('myCanvas');
}
function drawBase(id)
{
var canvas=document.getElementById(id);
if (canvas==null)
return false;
var context=canvas.getContext('2d');
context.fillStyle="#EEEEFF";
context.fillRect(0,0,800,500);
context.fillStyle="yellow";
context.strokeStyle="red";
context.lineWidth=1;
context.beginPath();
var dig=Math.PI/64;
var w=100;
// 在水平一行中绘制8个基本花型图案
for (n=1;n<=8;n++)
{
px=(2*n-1)/2*w;
for (i=0;i<=128;i++)
{
x1=px+x[sele][i];
y1=w/2-y[sele][i];
if (i==0)
{
context.moveTo(x1,y1);
bx=x1; by=y1;
}
else
context.lineTo(x1,y1);
}
}
context.lineTo(bx,by);
context.closePath();
context.stroke();
context.fill();
}
function drawRound(id,k)
{
var canvas=document.getElementById(id);
if (canvas==null)
return false;
var context=canvas.getContext('2d');
context.fillStyle="#EEEEFF";
context.fillRect(0,0,800,500);
context.fillStyle="yellow";
context.strokeStyle="red";
context.lineWidth=2;
context.beginPath();
var dig=Math.PI/64;
w=80; l=10;
// 进行多重环形变换
for (m=1;m<=k;m++)
for (n=1;n<=10;n++)
for (var i=0;i<=128;i++)
{
px=(2*n-1)/2*w;
py=(2*m-1)/2*w;
x1=px+x[sele][i];
y1=py-y[sele][i];
th=2*Math.PI*(w*10-x1)/(w*10);
x2=(l+y1)*Math.cos(th)+400;
y2=(l+y1)*Math.sin(th)+250;
if (i==0)
{
context.moveTo(x2,y2);
bx=x2; by=y2;
}
else
context.lineTo(x2,y2);
}
context.lineTo(bx,by);
context.closePath();
context.stroke();
context.fill();
}
</script>
</head>
<body>
<form name="frm">基本图案选择:
<select name="shape" onchange="seleShape();">
<option value="图案1">--请选择--</option>
<option value="图案1">图案1</option>
<option value="图案2">图案2</option>
<option value="图案3">图案3</option>
</select>
</form>
<button onClick="drawRound('myCanvas',1);">环形变换</button>
<button onClick="drawRound('myCanvas',2);">二重环形变换</button>
<button onClick="drawRound('myCanvas',3);">三重环形变换</button>
<br/><br/>
<canvas id="myCanvas" width="800" height="500">您的浏览器不支持canvas!</canvas>
</body>
</html>
将上述HTML代码保存到一个html文本文件中,再在浏览器中打开包含这段HTML代码的html文件,可以看到在浏览器窗口中,出现“基本图案选择”下拉列表框,提供三种基本图案的选择,还有“环形变换”、“二重环形变换”、“三重环形变换”这三个命令按钮。选定“基本图案”后,单击某个按钮,绘制出基本图案的相应环形变换图案。整个演示过程录屏后展示如图8所示。
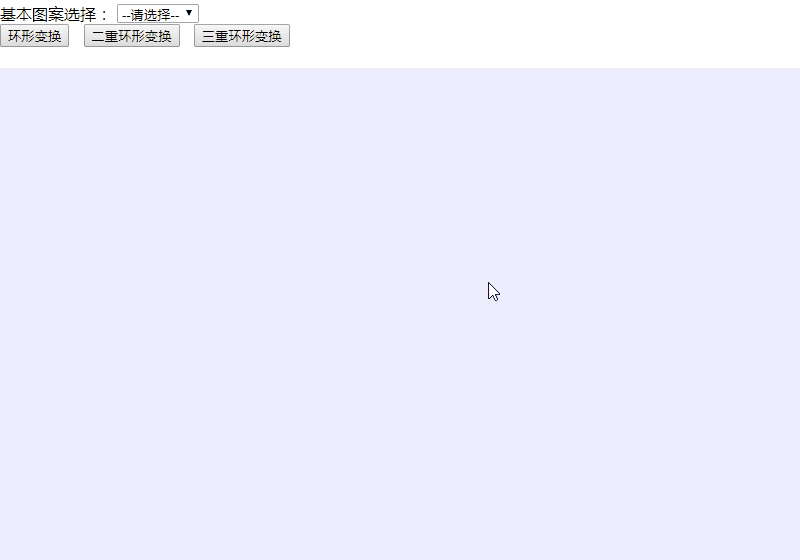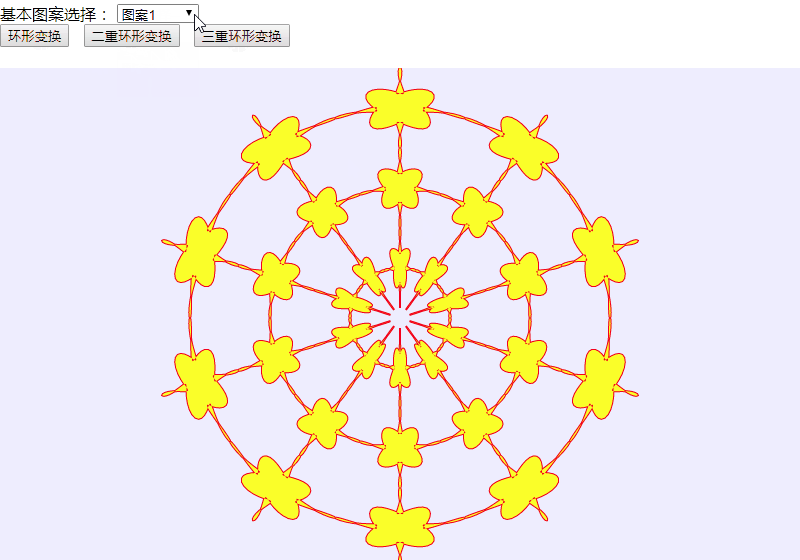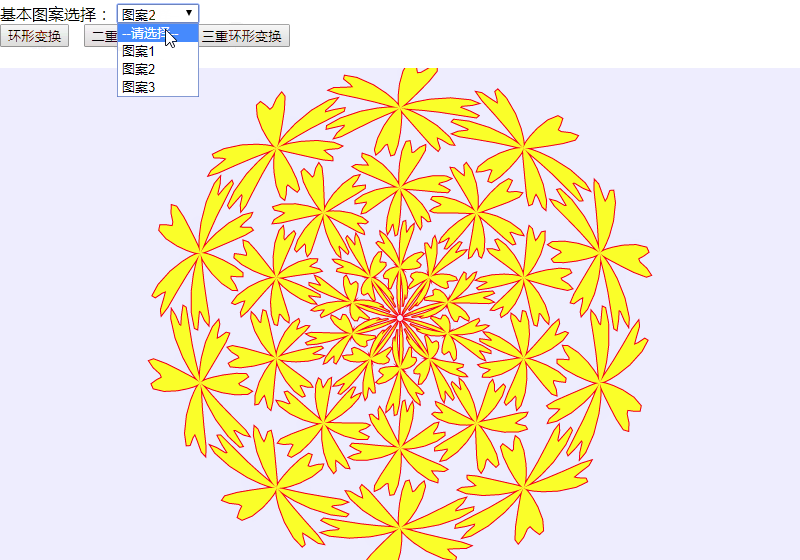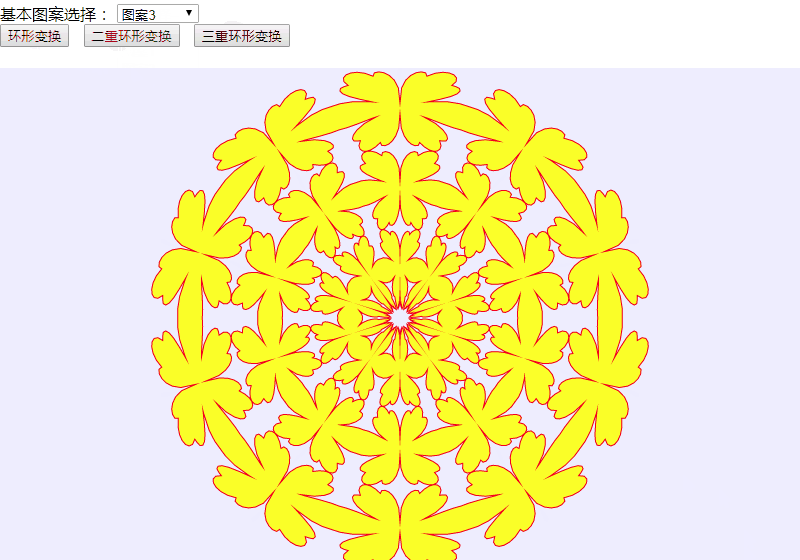
图8 可选择图案的环形变换
JavaScript图形实例:图形的扇形变换和环形变换的更多相关文章
- JavaScript图形实例:再谈IFS生成图形
在“JavaScript图形实例:迭代函数系统生成图形”一文中,我们介绍了采用迭代函数系统(Iterated Function System,IFS)创建分形图案的一些实例.在该文中,仿射变换函数W的 ...
- JavaScript图形实例:Canvas API
1.Canvas概述 Canvas API(画布)用于在网页实时生成图像,并且可以操作图像内容,基本上它是一个可以用JavaScript操作的位图(bitmap). 要使用HTML5在浏览器窗口中绘制 ...
- JavaScript图形实例:线段构图
在“JavaScript图形实例:四瓣花型图案”和“JavaScript图形实例:蝴蝶结图案”中,我们绘制图形时,主要采用的方法是先根据给定的曲线参数方程计算出两点坐标,然后将两点用线段连接起来,线段 ...
- JavaScript图形实例:随机SierPinski三角形
在“JavaScript图形实例:SierPinski三角形”中,我们介绍了SierPinski三角形的基本绘制方法,在“JavaScript图形实例:迭代函数系统生成图形”一文中,介绍了采用IFS方 ...
- JavaScript动画实例:李萨如曲线
在“JavaScript图形实例:阿基米德螺线”和“JavaScript图形实例:曲线方程”中,我们学习了利用曲线的方程绘制曲线的方法.如果想看看曲线是怎样绘制出来的,怎么办呢?编写简单的动画,就可以 ...
- JavaScript动画实例:递归分形图动态展示
在“JavaScript图形实例:SierPinski三角形” 和“JavaScript图形实例:Levy曲线及其变形”等文章中我们介绍了通过递归生成分形图形的方法.我们可以将绘制的分形图形每隔一定的 ...
- JavaScript动画实例:曲线的绘制
在“JavaScript图形实例:曲线方程”一文中,我们给出了15个曲线方程绘制图形的实例.这些曲线都是根据其曲线方程,在[0,2π]区间取一系列角度值,根据给定角度值计算对应的各点坐标,然后在计算出 ...
- JavaScript小实例:拖拽应用(二)
经常在网站别人的网站的注册页中看到一个拖拽验证的效果,就是它的验证码刚开始不出来,而是有一个拖拽的条,你必须将这个拖拽条拖到底,验证码才出来,说了感觉跟没说一样,你还是不理解,好吧,我给个图你看看: ...
- javascript小实例,拖拽应用(一)
前面我们将了一下拖拽的基本思想,理论是有了,那实践呢,可以运用到什么地方呢?下面就给大家带来一个用拖拽思想写的一个小实例,供大家参考,大致效果看下图: 就是这样一个简单的一个拖拽条,你可以把它理解为滚 ...
随机推荐
- Windows异常处理机制简介
windows系统里,为了保证系统内核的强壮和稳定,为了保证用户程序的强壮和稳定,提供了异常处理机制,来帮助程序员和系统使用人员处理异常.简单来说,当CPU执行代码时,发生异常,会把异常告知操作系统, ...
- Jenkins 更改工作目录;
更改 Jenkins 工作目录:如果使用 tomcat 加载的 war包形式启动 默认配置文件 /root/.jenkins Jenkins 默认配置文件 /root/.jenkins/config ...
- word collocations中文版(信息检索)
虽然说是大作业,也做了好几天,但是完全没有什么实际价值...就是把现有的东西东拼西凑一下,发现跑的特别慢还搞了个多核 写这篇blog纯属是我吃饱了没事干,记录一下装env的蛋疼 首先我们是在pytho ...
- cf 1037D BFS
$des$一个 n 个点 m 条边的无向连通图从 1 号点开始 bfs,可能得到的 bfs 序有很多,取决于出边的访问顺序.现在给出一个 1 到 n 的排列,判断是否可能是一个 bfs 序. $sol ...
- js 中的方法注入(aop)
js 中的方法注入 java中很多框架支持 apo 的注入, js中也可以类似的进行实现 主要是通过扩展js中方法的老祖 Function 对象来进行实现. Function.prototype.af ...
- typescript 错误记录
经常遇到 typescript 的编译错误,虽然可以绕过去,不过既然采用了,还是解决问题,了解其中的思想比较重要. 一般遇到错误码 error TS2304: Cannot find name ... ...
- Pytest权威教程15-运行Nose用例
目录 运行Nose用例 使用方法 支持的nose风格 不支持的习语/已知问题 返回: Pytest权威教程 运行Nose用例 Pytest基本支持运行Nose框架格式的测试用例. 使用方法 后安装py ...
- LeetCode之打家劫舍
1. 问题 在一条直线上,有n个房屋,每个房屋中有数量不等的财宝,有一个盗 贼希望从房屋中盗取财宝,由于房屋中有报警器,如果同时从相邻的两个房屋中盗取财宝就会触发报警器.问在不触发报警器的前提下,最多 ...
- 【CSP模拟赛】避难向导(倍增lca&树的直径)
耐力OIer,一天7篇博客 题目描述 “特大新闻,特大新闻!全国爆发了一种极其可怕的病毒,已经开始在各个城市 中传播开来!全国陷入了巨大的危机!大量居民陷入恐慌,想要逃到其它城市以 避难!经调查显示, ...
- CPU突然飙升到300%,Dubbo活动线程数直接飙到1000
转:https://mp.weixin.qq.com/s/-lSiVDfqYrKk_w-xitYBhA 背景:新功能开发测试完成后,准备发布上线,当发布完第三台机器时,监控显示其中一台机器CPU突然飙 ...
