Python实现Newton和lagrange插值

一、介绍
Newton和lagrange插值：给出一组数据进行Newton和lagrange插值，同时将结果用plot呈现出来
1、首先是Lagrange插值：
根据插值的方法，先对每次的结果求积，在对结果求和，完成插值。

2、newton插值：
先要建立差商表，差商表的建立的时候，每次减去的x[0]都是对角的元素，因此需要注意。

二、实现

import matplotlib.pyplot as plt
import math

# ===================================================  lagrange插值  =================================================================
def lagrange(x_, y, a):
    """
    获取拉格朗日插值
    :param x_: x的列表值
    :param y: y的列表值
    :param a: 需要插值的数
    :return: 返回插值结果
    """
    ans = 0.0
    for i in range(len(y)):
        t_ = y[i]
        for j in range(len(y)):
            if i != j:
                t_ *= (a - x_[j]) / (x_[i] - x_[j])
        ans += t_
    return ans

# ===================================================  newton插值  =================================================================
def table(x_, y):
    """
    获取牛顿插值表
    :param x_: x列表的值
    :param y: y列表的值
    :return: 返回插值表
    """
    quotient = [[0] * len(x_) for _ in range(len(x_))]
    for n_ in range(len(x_)):
        quotient[n_][0] = y[n_]
    for i in range(1, len(x_)):
        for j in range(i, len(x_)):
            # j - i 确定了对角线的元素
            quotient[j][i] = (quotient[j][i - 1] - quotient[j - 1][i - 1]) / (x_[j] - x_[j - i])
    return quotient

def get_corner(result):
    """
    通过插值表获取对角线元素
    :param result: 插值表的结果
    :return: 对角线元素
    """
    link = []
    for i in range(len(result)):
        link.append(result[i][i])
    return link

def newton(data_set, x_p, x_7):
    """
    牛顿插值结果
    :param data_set: 求解的问题的对角线
    :param x_p: 输入的值
    :param x_7: 原始的x的列表值
    :return: 牛顿插值结果
    """
    result = data_set[0]
    for i in range(1, len(data_set)):
        p = data_set[i]
        for j in range(i):
            p *= (x_p - x_7[j])
        result += p
    return result

# ============================================================== 画图 =====================================================
def draw_picture(x_list, y_list, node):
    plt.title("newton")
    plt.xlabel("x")
    plt.ylabel("y")
    # plt.plot(x_list, y_list, color="red")
    for i in range(len(x_list)):
        plt.scatter(x_list[i], y_list[i], color="purple", linewidths=2)
    plt.scatter(node[0], node[1], color="blue", linewidth=2)
    plt.show()

if __name__ == '__main__':
    x = 0.54
    x_1 = [0.4, 0.5, 0.6, 0.7, 0.8]
    y_1 = [-0.9163, -0.6931, -0.5108, -0.3567, -0.2231]
    middle = table(x_1, y_1)
    n = get_corner(middle)
    newton = newton(n, x, x_1)
    lagrange = lagrange(x_1, y_1, 0.54)
    print("真值:{}".format(math.log(0.54, math.e)))
    print("拉格朗日插值:{}".format(lagrange))
    print("牛顿插值:{}".format(newton))
    #  画图
    draw_picture(x_1, y_1, (x, newton))

三、结果
1、插值结果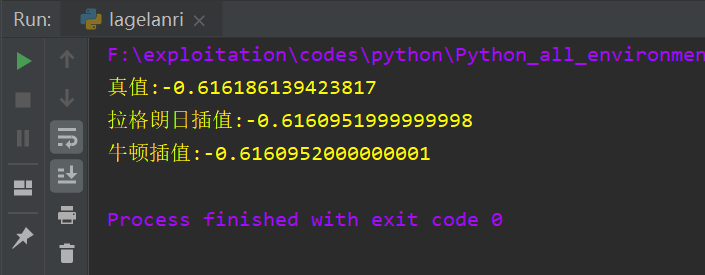

2、画图结果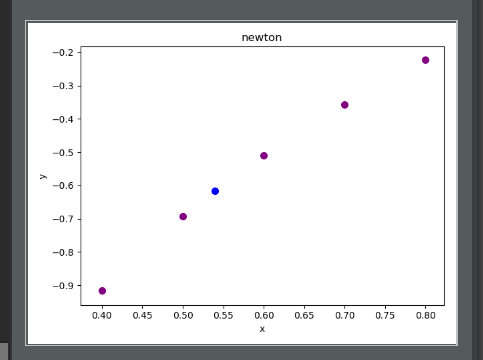

四、总结
Newton和lagrange可以参考一下数值分析的课本，根据课本的公式来进行插值分析。具体过程也在代码中给出。