（DP）51NOD 1183 编辑距离

编辑距离，又称Levenshtein距离（也叫做Edit Distance），是指两个字串之间，由一个转成另一个所需的最少编辑操作次数。许可的编辑操作包括将一个字符替换成另一个字符，插入一个字符，删除一个字符。

例如将kitten一字转成sitting：

sitten （k->s）

sittin （e->i）

sitting （->g）

所以kitten和sitting的编辑距离是3。俄罗斯科学家Vladimir Levenshtein在1965年提出这个概念。

给出两个字符串a,b，求a和b的编辑距离。

 

Input

第1行：字符串a(a的长度 <= 1000)。
第2行：字符串b(b的长度 <= 1000)。

Output

输出a和b的编辑距离

Input示例

kitten
sitting

Output示例

3
解：
具体介绍：https://www.51nod.com/tutorial/course.html#!courseId=3
我们以矩阵形式实现了教程中的比较思想。
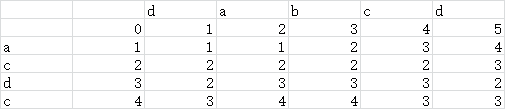
以字符串dabcd和acdc为例，演示流程：
(第二行与第二列预置，之后的数字由其对应行列字母与上，左，左上数字决定。
 　　具体操作：首先比较对应行列字母，若一样则填入左上数据，
　　　　　　　　　　　　　　　　　　 否则填入上，左，左上数字的最小值加一。)

 #include<stdio.h>

 char a[], b[];
 int dp[][];

 int min(int a, int b, int c)
 {
     b = b < a ? b : a;
     return (c < b ? c : b);
 }

 int main()
 {
     while (scanf_s("%s%s", a, , b, ) != EOF)
     {
         int i, j;
         for (i = ; i ==  || a[i - ] != ; i++)
             for (j = ; j ==  || b[j - ] != ; j++)
                 if (i ==  || j == ) dp[i][j] = i | j;
                 else if (a[i - ] == b[j - ]) dp[i][j] = dp[i - ][j - ];
                 else dp[i][j] = min(dp[i - ][j - ], dp[i - ][j], dp[i][j - ]) + ;
         printf("%d\n", dp[i - ][j - ]);
     }
     return ;
 }

由于该方法顺序的检索顺序，我们可以优化空间消耗，减小数组dp的大小：

 #include<stdio.h>

 char a[], b[];
 int dp[][];

 int min(int a, int b, int c)
 {
     b = b < a ? b : a;
     return (c < b ? c : b);
 }

 int main()
 {
     while (scanf_s("%s%s", a, , b, ) != EOF)
     {
         int i, j;
         for (i = ;  != a[i]; i++) dp[][i + ] = i + ;
         for (i = ;  != a[i - ]; i++)
         {
             dp[i & ][] = i;
             for (j = ;  != b[j - ]; j++)
             {
                 if (a[i - ] == b[j - ]) dp[i & ][j] = dp[i +  & ][j - ];
                 else dp[i & ][j] = min(dp[i & ][j - ], dp[i +  & ][j - ], dp[i +  & ][j]) + ;
             }
         }
         printf("%d\n", dp[i +  & ][j - ]);
     }
     return ;
 }