求 LCA 的三种方法

(YYL: LCA 有三种求法, 你们都知道么?)

(众神犇: 这哪里来的傻叉...)

1. 树上倍增

对于求 LCA, 最朴素的方法是"让两个点一起往上爬, 直到相遇", "如果一开始不在同一深度, 先爬到同一深度". 树上倍增求 LCA 的方法同样基于这个道理, 只不过利用了倍增思想从而加速了"向上爬"的操作. 也就是说, 每次向上爬的高度不是 1, 而是 2 的幂.

我们用 $f(i, j)$ 表示从节点 $i$ 向上爬 $2^j$ 的高度所到达的节点, 则 $f(i, 0)$ 就代表节点 $i$ 的父节点. 那么对于任意的 $f(i, j), j > 0$, 有

$f(i, j) = f(f(i, j-1), j-1)$.

当我们要求两点的 LCA 时, 先让它们到同一高度. 这个过程我们使用二进制拆分来加速. 比如当两点高度相差 $5$ 时, $(5)_{10} = (101)_2$, 那么我们就让高度较小的那个节点先往上爬 $2^2 = 4$ 步, 再往上 $2^0 = 1$ 步. 此时两点即在同一高度.

如果爬到同一高度后两点相同, 显然这个点就是它们的 LCA, 直接返回即可.

如果两点不同, 就一起往上爬. 这是一个无限逼近的过程, 直到找到它们的 LCA 的子节点为止. 详见代码.

 for (int i = ; i <= n; ++i)
     lg[i] = lg[i - ] + ( << lg[i - ] +  == i);

 int lca(int x, int y) {
     if (dep[x] < dep[y])
         swap(x, y);
     while (dep[x] > dep[y])
     x = f[x][lg[dep[x] - dep[y]]];
     if (x == y)
         return x;
     for (int k = lg[dep[x]]; k >= ; --k)
         if (f[x][k] != f[y][k])
             x = f[x][k], y = f[y][k];
     return f[x][];
 }

(上面的代码预先算出了 $log_2 (n)$ 的值, 从而简化了代码.)

2. Tarjan 算法

Tarjan 算法建立在 DFS 的基础上.

假如我们正在遍历节点 x, 那么根据所有节点各自与 x 的 LCA 是谁, 我们可以将节点进行分类: x 与 x 的兄弟节点的 LCA 是 x 的父亲, x 与 x 的父亲的兄弟节点的 LCA 是 x 的父亲的父亲, x 与 x 的父亲的父亲的兄弟节点的 LCA 是 x 的父亲的父亲的父亲... 将这些类别各自归入不同的集合中, 如果我们能够维护好这些集合, 就能够很轻松地处理有关 x 节点的 LCA 的询问. 显然我们可以使用并查集来维护.

Tarjan 算法的大致步骤如下:

1. 遍历 x 节点的子节点. 对于 x 节点的每个子节点, 该子节点遍历结束之后, 将其整棵子树合并到 x, 并保证合并之后祖先为 x;

2. 将 x 标记为已遍历;

3. 处理有关 x 的询问. 对于询问 (x, y), 如果 y 节点已遍历, 则 x 与 y 的 LCA 就是 y 节点所在集合的祖先; 否则, 将其推迟到遍历 y 时再处理.

代码如下:

 void tarjan(int u) {
     fa[u] = u;

     int i, v;
     for (i = ; i < tree[u].size(); i++) {
         v = tree[u][i];
         tarjan(v);
         fa[findset(v)] = u;
     }

     vis[u] = true;

     for (i = ; i < query[u].size(); i++) {
         if (vis[query[u][i]]) {
             cnt[findset(query[u][i])]++;
         }
     }
 }

(对于保证合并之后集合祖先为 x 这一步骤, 网络上的代码大多使用了一个 ancestor 数组来记录集合的祖先是谁. 原因是如果使用并查集的带秩合并, 合并两个集合之后不好确定根节点到底是谁. 但是带秩合并在有路径压缩的情况下作用有限, 所以这里取消了带秩合并而直接使用 fa[findset(v)] = u 来保证集合的祖先为 u.)

3. LCA 转 RMQ

树上的一些问题可以转化为对树的 DFS 序列的操作. 比如对于这样一棵树:

(图片来自 http://scturtle.is-programmer.com/posts/30055.html)

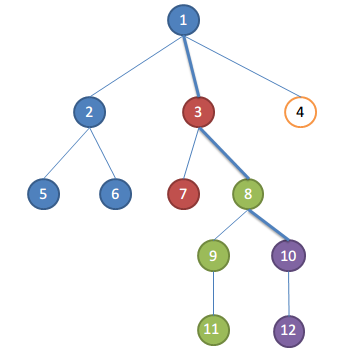
对于以 3 这个节点为根的整棵子树, 其 DFS 序列为: 3 7 3 8 9 11 9 8 10 12 10 8 3.

假如我们要询问 7 和 12 的 LCA, 我们找到 7 和 12 分别第一次出现的位置, 然后在这一个区间内找到深度最小的那个节点, 也就是节点 3, 显然它就是 7 和 12 的 LCA.

记 DFS 序列为 $S[1...2n]$, 节点 $x$ 在序列 $S$ 中第一次出现的位置为 $E[x]$, 用 $RMQ(L, R)$ 表示序列 $S$ 中深度最小的那个节点. 则

$LCA(u, v) = RMQ(E[u], E[v])$

代码略. DFS + RMQ 的普通做法即可(ST, 线段树等等).