洛谷P4009 汽车加油行驶问题

题目描述

给定一个 N \times NN×N 的方形网格，设其左上角为起点◎，坐标(1,1)(1,1)，XX 轴向右为正， YY 轴向下为正，每个方格边长为 11 ，如图所示。

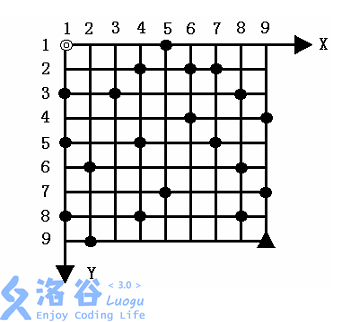
一辆汽车从起点◎出发驶向右下角终点▲，其坐标为 (N,N)(N,N)。

在若干个网格交叉点处，设置了油库，可供汽车在行驶途中加油。汽车在行驶过程中应遵守如下规则:

1. 汽车只能沿网格边行驶，装满油后能行驶 KK 条网格边。出发时汽车已装满油，在起点与终点处不设油库。

2. 汽车经过一条网格边时，若其 XX 坐标或 YY 坐标减小，则应付费用 BB ，否则免付费用。

3. 汽车在行驶过程中遇油库则应加满油并付加油费用 AA。

4. 在需要时可在网格点处增设油库，并付增设油库费用 CC(不含加油费用AA )。

5. N,K,A,B,CN,K,A,B,C 均为正整数， 且满足约束: 2\leq N\leq 100,2 \leq K \leq 102≤N≤100,2≤K≤10。

设计一个算法，求出汽车从起点出发到达终点所付的最小费用。

输入输出格式

输入格式：

文件的第一行是 N,K,A,B,CN,K,A,B,C 的值。

第二行起是一个N\times NN×N 的 0-10−1 方阵,每行 NN 个值,至 N+1N+1 行结束。

方阵的第 ii 行第 jj 列处的值为 11 表示在网格交叉点 (i,j)(i,j) 处设置了一个油库,为 00 时表示未设油库。各行相邻两个数以空格分隔。

输出格式：

程序运行结束时,输出最小费用。

输入输出样例

输入样例#1：

9 3 2 3 6
0 0 0 0 1 0 0 0 0
0 0 0 1 0 1 1 0 0
1 0 1 0 0 0 0 1 0
0 0 0 0 0 1 0 0 1
1 0 0 1 0 0 1 0 0
0 1 0 0 0 0 0 1 0
0 0 0 0 1 0 0 0 1
1 0 0 1 0 0 0 1 0
0 1 0 0 0 0 0 0 0

输出样例#1：

12

分层最短路板子题，讲在i行，j列，还剩k油为一个状态，其中建出这个点为k*n*n+i*n+j然后分出加油和跑路，跑一边SPFA即可

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <cstdlib>
#include <queue>
#include <stack>
#include <vector>
using namespace std;
#define MAXN 200100
#define INF 10000009
#define MOD 10000007
#define LL long long
#define in(a) a=read()
#define REP(i,k,n) for(int i=k;i<=n;i++)
#define DREP(i,k,n) for(int i=k;i>=n;i--)
#define cl(a) memset(a,0,sizeof(a))
inline int read(){
    int x=,f=;char ch=getchar();
    for(;!isdigit(ch);ch=getchar()) if(ch=='-') f=-;
    for(;isdigit(ch);ch=getchar()) x=x*+ch-'';
    return x*f;
}
inline void out(int x){
    if(x<) putchar('-'),x=-x;
    if(x>) out(x/);
    putchar(x%+'');
}
int n,k,a,b,c;
deque <int> Q;
int ans=;
int dis[MAXN],vis[MAXN];
int total=,head[MAXN<<],nxt[MAXN<<],to[MAXN<<],val[MAXN<<];
inline int calc(int l,int i,int j){
    return n*n*l+n*i+j;
}
inline void adl(int a,int b,int c){
    total++;
    to[total]=b;
    val[total]=c;
    nxt[total]=head[a];
    head[a]=total;
    return ;
}
inline void SPFA(){
    memset(dis,,sizeof(dis));
    Q.push_back(calc(k,,));
    dis[calc(k,,)]=;
    vis[calc(k,,)]=;
    while(!Q.empty()){
        int u=Q.front();
        Q.pop_front();
        vis[u]=;
        for(int e=head[u];e;e=nxt[e])
            if(dis[to[e]]>dis[u]+val[e]){
                dis[to[e]]=dis[u]+val[e];
                if(vis[to[e]])  continue;
                vis[to[e]]=;
                if(!Q.empty())
                    if(dis[to[e]]<dis[Q.front()])  Q.push_front(to[e]);
                    else  Q.push_back(to[e]);
                else  Q.push_back(to[e]);
            }
    }
    return ;
}
int main(){
    in(n);in(k);in(a);in(b);in(c);
    REP(i,,n-)
        REP(j,,n-){
            int x;
            in(x);
            if(x || (!i && !j)){
                REP(l,,k-)  adl(calc(l,i,j),calc(k,i,j),a);
                if(i!=n-)  adl(calc(k,i,j),calc(k-,i+,j),);
                if(j!=n-)  adl(calc(k,i,j),calc(k-,i,j+),);
                if(i)  adl(calc(k,i,j),calc(k-,i-,j),b);
                if(j)  adl(calc(k,i,j),calc(k-,i,j-),b);
            }
            else{
                REP(l,,k-)  adl(calc(l,i,j),calc(k,i,j),a+c);
                REP(l,,k){
                    if(i!=n-)  adl(calc(l,i,j),calc(l-,i+,j),);
                    if(j!=n-)  adl(calc(l,i,j),calc(l-,i,j+),);
                    if(i)  adl(calc(l,i,j),calc(l-,i-,j),b);
                    if(j)  adl(calc(l,i,j),calc(l-,i,j-),b);
                }
            }
        }
    SPFA();
    ans=INF;
    REP(i,,k)  ans=min(ans,dis[calc(i,n-,n-)]);
    out(ans);
    return ;
}