KL散度的理解（GAN网络的优化）

原文地址Count Bayesie
这篇文章是博客Count Bayesie上的文章Kullback-Leibler Divergence Explained 的学习笔记，原文对 KL散度 的概念诠释得非常清晰易懂，建议阅读

相对熵，又称KL散度( Kullback–Leibler divergence)，是描述两个概率分布P和Q差异的一种方法。它是非对称的，这意味着D(P||Q) ≠ D(Q||P)。

KL散度的计算

衡量近似分布带来的信息损失。 
KL散度的计算公式其实是熵计算公式的简单变形,在原有概率分布 p上，加入我们的近似概率分布 q，计算他们的每个取值对应对数的差：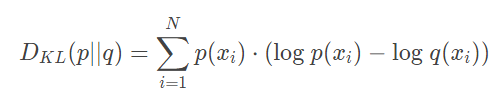

换句话说，KL散度计算的就是数据的原分布与近似分布的概率的对数差的期望值。 
在对数以2为底时，log⁡2 ，可以理解为“我们损失了多少位的信息” 
写成期望形式 ：

The more common way to see KL divergence written is as follows:

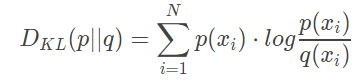
With KL divergence we can calculate exactly how much information is lost when we approximate one distribution with another.

散度不是距离

因为KL散度不具有交换性，所以不能理解为“距离”的概念，衡量的并不是两个分布在空间中的远近，更准确的理解还是衡量一个分布相比另一个分布的信息损失(infomation lost)

使用KL散度进行优化

通过不断改变预估分布的参数，我们可以得到不同的KL散度的值。 
在某个变化范围内，KL散度取到最小值的时候，对应的参数是我们想要的最优参数。 
这就是使用KL散度优化的过程。

参考CodenameNC的博客

GAN网络使用KL散度