机器学习之K近邻算法

K 近邻 (K-nearest neighbor, KNN) 算法直接作用于带标记的样本，属于有监督的算法。它的核心思想基本上就是 近朱者赤，近墨者黑。

它与其他分类算法最大的不同是，它是一种“懒惰”的学习算法 (lazy learning)，因为实际上它并没有“训练”的过程，也不产生一个真实意义上的“模型”，而只是一字不差地将所有训练样本保存起来，等到需要对新样本进行分类的时候，将新样本与所有训练样本进行比较，找出与其距离最接近的 k 个样本，然后基于这 k 个“邻居”所属的类别进行投票，决定分类结果。

距离度量

常用的距离计算方式如下讨论。

欧氏距离

欧式距离 (Euclidean distance)是最易于理解的一种距离计算方法，源自欧氏空间中两点间的距离公式，指 m 维空间中两个点之间的真实距离。

它的一个缺点是对所有变量同等看待，而没有考虑到不同变量由于量纲不同（如“身高”和“体重”），在计算中应该给予不同的重要程度。因此，在实际使用中应该先对所有变量进行标准化处理后再计算距离。

常用的标准化处理方式包括 Z-score 标准化、最大-最小值标准化和正则化等。

点 \(P_1(x_{11},x_{12},\cdots,x_{1n})\)与\(P_2(x_{21},x_{22},\cdots,x_{2n})\)之间的欧氏距离为：

\[d_{12}=\sqrt{\sum^n_{k=1}{({x_{1k}-x_{2k})}^2}}
\]

使用 Python 实现计算欧式距离的代码如下：

# 构造样本点
import numpy as np
x=np.array([1,1])
y=np.array([4,5])
# 计算欧氏距离
from math import *
def e_distance(x,y):
    return sqrt(sum(pow(a-b,2) for a,b in zip(x,y)))
print(e_distance(x,y))

曼哈顿距离

曼哈顿距离 (Manhattan distance)，也就是在欧几里得空间的固定直角坐标系上两点所形成的线段对轴产生的投影的距离综合。

点 \(P_1(x_{11},x_{12},\cdots,x_{1n})\)与\(P_2(x_{21},x_{22},\cdots,x_{2n})\)之间的曼哈顿距离为：

\[d_{12}=\sum_{k=1}^n{|x_{1k}-x_{2k}|}
\]

使用 Python 实现计算曼哈顿距离的代码如下：

# 构造样本点
import numpy as np
x=np.array([1,1])
y=np.array([4,5])
# 计算曼哈顿距离
from math import *
def m_distance(x,y):
    return sum(abs(x-y))
print(m_distance(x,y))

切比雪夫距离

类似国际象棋中国王的移动，国王走一步能够移动到相邻的8个方格中的任意一个。那么国王从格子 \((x_1,y_1)\) 走到格子 \((x_2,y_2)\) 最少需要走 \(max(|x_2-x_1|,|y_2-y_1|)\) 步。切比雪夫距离 (Chebyshev distance)就是类似这种的度量方法。

点 \(P_1(x_{11},x_{12},\cdots,x_{1n})\)与\(P_2(x_{21},x_{22},\cdots,x_{2n})\)之间的切比雪夫距离为：

\[d_{12}=\sum_{k=1}^n{|x_{1k}-x_{2k}|}
\]

使用 Python 实现计算切比雪夫距离的代码如下：

# 构造样本点
import numpy as np
x=np.array([1,1])
y=np.array([4,5])
# 计算切比雪夫距离
from math import *
def q_distance(x,y):
    return abs(x-y).max()
print(q_distance(x,y))

夹角余弦距离

夹角余弦距离 (Cosine distance)，是用向量空间中两个向量夹角的余弦值作为衡量两个个体间差异的大小的度量。

夹角余弦取值范围为 \([-1,1]\) 。夹角余弦越大表示两个向量的夹角越小，也就是这两个向量越相近。

需要注意的是，夹角余弦距离只考虑两个样本（向量）之间的“方向一致性”，而不考虑强度大小。比如向量 \((1,2)\)和 \((100,200)\) 的余弦距离为1，方向完全一致，但它们的强度相差甚远。夹角余弦距离常用在对文本之间的距离计算。

点 \(P_1(x_{11},x_{12},\cdots,x_{1n})\)与\(P_2(x_{21},x_{22},\cdots,x_{2n})\)之间的夹角余弦距离为：

\[cos (\theta)=\frac{\sum_{k=1}^n{X_{1k}X_{2k} } }{\sqrt{\sum^n_{k=1}} { {X_{1k} }^2}\sqrt{\sum^n_{k=1} } { {X_{2k} }^2} }
\]

使用 Python 实现计算夹角余弦距离的代码如下：

# 构造样本点
import numpy as np
x=np.array([1,1])
y=np.array([4,5])
# 计算夹角余弦距离
from math import *
def cos_distance(x,y):
    return np.dot(x,y)/(np.linalg.norm(x)*np.linalg.norm(y))
print(cos_distance(x,y))

算法过程

（1）计算距离： 给定待分类的样本，计算该样本与其他样本的距离。

（2）距离排序：将计算出的距离降序排列。

（3）选择 k 个近邻：根据排序结果，选择距离最近的 k 个样本作为待分类样本的 k 个近邻。

（4）决定分类： 找出 k 个近邻的主要类别，即按投票方式决定待分类样本的类别。

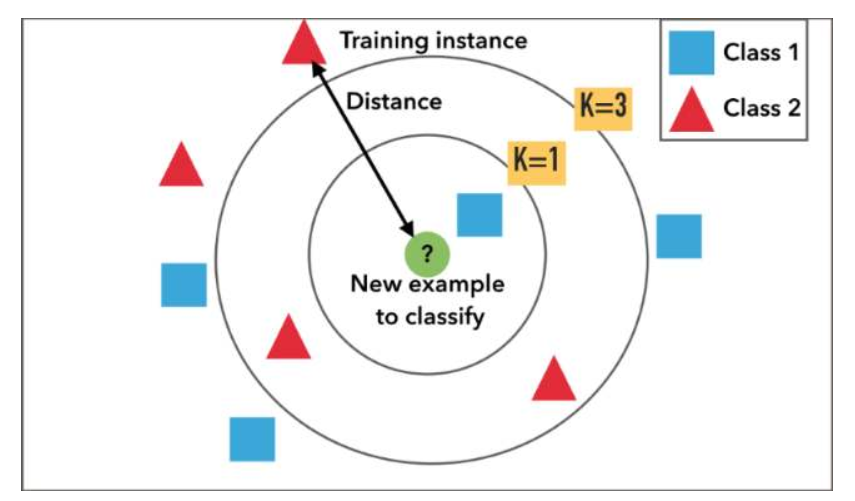
K 值选择

k 值的大小会对分类结果产生巨大影响。

如果 k 设得太小，相当于说我们只用较小的邻域来对决定待分类样本的类别，此时分类结果只取决于待分类样本点最近的少数几个样本，在这种情况下，算法在训练集上的误差会很小，但在新样本上的误差会变大。存在过拟合的风险。

如果 k 设得太大，相当于说我们用较大的邻域来做出分类决定，此时距离待分类样本较远的样本点也会对分类结果起作用，这样做的优点是不容易产生过拟合，但模型的泛化能力也会大大降低。

如何选择恰当的 k 值大小，需要反复尝试和验证。

分类决策

通常情况下，最终待分类样本的分类只需要根据所选择的 k 个近邻投票决定即可，但有时我们也可以根据实际需要，对决策的过程进行改进。

常见的优化方式有：对距离加权和对样本加权。

优缺点

优点：

（1）原理简单，易于理解，实现方便，不需要训练的过程。

（2）特别适用于多分类问题，如根据基因的特征判断基因的功能。

（3）对异常值不敏感。

缺点：

（1）每次进行预测都要对所有样本进行扫描和计算距离，因此当样本集很大时，计算量会很大。

（2）需要存储所有的样本。

（3）结果的可解释性差，无法给出规则。

（4）数据集中如果含有缺失值，需要特殊处理。

算法优化思路

基本的 KNN 算法有两个致命的短板：需要存储所有的训练样本；每次预测需要在所有训练样本上计算一遍。

在真实业务场景中，这种方法几乎是不可行的。

算法角度优化

思路1

对训练样本集重新组织整理，分成若干个小样本组，使得每次的计算压缩在接近待分类样本的小范围邻域内。这种方法可以避免对全样本计算，但不能减少存储量。代表算法有快速搜索近邻法。

思路2

在原样本中挑出对分类计算有效的样本，使样本总数合理地减少，这样既减少计算量，也减少存储量。代表算法有剪辑近邻法与压缩近邻法。

数据结构角度优化

一些特别的数据结构可以使得最近邻搜索速度提升。比如**KD 树 (K-dimension tree) **。

硬件角度优化

可以看出，KNN 计算的过程是高度并行的，非常适合 GPU 处理。

Demo

使用 KNN 对 Iris 数据集进行分类。

Jupyter Notebook 链接为：KNN-Iris

【References】

[1] 裔隽，张怿檬，张目清等．Python机器学习实战[M]．北京：科学技术文献出版社，2018