Bezier画线算法
编译器:VS2013
描述:Bezier画线是利用导数相同拼接曲线,使曲线十分光滑,而不是随意拼接观赏性很差
主函数段
#include "stdafx.h"
#include<stdio.h>
#include"graphics.h"
#include<stdlib.h>
#include<math.h> //函数声明
void Bezier4(int a[]);//四个控制点画出曲线
void Beziern(int a[], int N);//N个点画出曲线
int factorial(int n);//利用递归求出阶乘 int main()
{
int *p, N,gdriver = DETECT, gmove, i; printf("please input the number of point\n");
scanf_s("%d", &N); p = (int *)malloc( * N*sizeof(int)); printf("please input the coordinate:\n");
for (i = ; i < * N; i += )
scanf_s("%d%d", &p[i], &p[i + ]); initgraph(&gdriver, &gmove, ""); //画出多边形
for (i = ; i < *N-; i += )
line(p[i], p[i + ], p[i + ], p[i + ]); Beziern(p, N); system("pause"); closegraph(); return ;
}
Bezier画线函数
//N个点画出曲线
void Beziern(int a[], int N)
{
double t, X1 = a[], Y1 = a[];
int k,i; for (t = ; t <= ; t += 0.02)
{
putpixel(X1, Y1, YELLOW); X1 = , Y1 = ; for (i=,k = ; k<N; i+=,k ++)
{
X1 += 1.0*a[i] * factorial(N-) / factorial(k) / factorial(N- - k)*pow(t, k)*pow( - t, N- - k);//pow函数为求指数的函数
Y1 += 1.0*a[i+] * factorial(N-) / factorial(k) / factorial(N- - k)*pow(t, k)*pow( - t, N -- k);
} }
} //利用递归求出阶乘
inline int factorial(int n)
{
if (n > )
return n*factorial(n - );
else
return ;
}
结果:
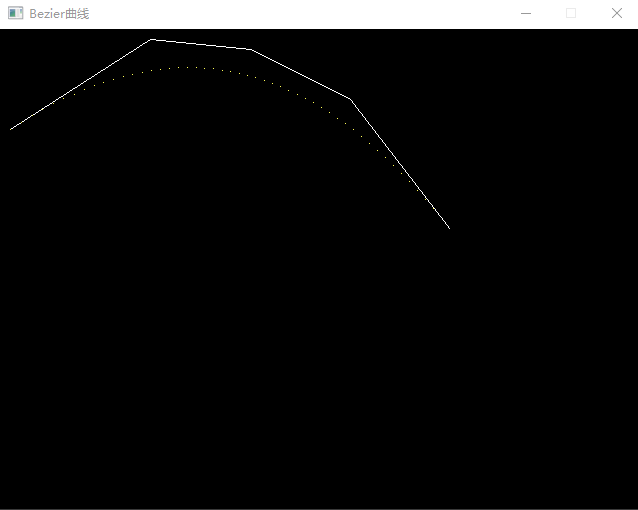
Bezier画线算法的更多相关文章
- 两种画线算法(DDA&Bersenham)
DDA(digital differential analyzer) 由直线的斜截式方程引入 对于正斜率的线段,如果斜率<=1,则以单位x间隔(δx=1)取样,并逐个计算每一个y值 Yk+1 = ...
- Bresenham画线算法
[Bresenham画线算法] Bresenham是一种光栅化算法.不仅可以用于画线,也可以用用画圆及其它曲线. 通过lower与upper的差,可以知道哪一个点更接近线段: 参考:<计算机图形 ...
- 中点Brehensam画线算法
#include<stdio.h> #include<stdlib.h> #include"graphics.h" //函数声明 void MidBreha ...
- 计算机图形学(二)输出图元_3_画线算法_2_DDA算法
DDA算法 数字微分分析仪(digital differential analyzer, DDA)方法是一种线段扫描转换算法.基于使用等式(3.4)或等式(3.5)计算的&x或& ...
- DDA画线算法
#include<stdio.h> #include"graphics.h" #include<math.h> #include<stdlib.h&g ...
- Bresenham直线算法与画圆算法
在我们内部开发使用的一个工具中,我们需要几乎从 0 开始实现一个高效的二维图像渲染引擎.比较幸运的是,我们只需要画直线.圆以及矩形,其中比较复杂的是画直线和圆.画直线和圆已经有非常多的成熟的算法了,我 ...
- 计算机图形学DDA画线法+中点画线法+Bresenham画线法
#include <cstdio> #include <cstring> #include <conio.h> #include <graphics.h> ...
- 画线函数Glib_Line算法的研究
在这里首先先简单把我对函数的功能的理解阐述一下,方便后面的分析:Glib_Line函数实现的功能是通过参数给定(x1,y1,x2,y2,color),来确定起点(x1,y1)和终点(x2,y2)两 ...
- Android中Path类的lineTo方法和quadTo方法画线的区别
转载:http://blog.csdn.net/stevenhu_223/article/details/9229337 当我们需要在屏幕上形成画线时,Path类的应用是必不可少的,而Path类的li ...
随机推荐
- strtus2 文件上传
struts2和spring mvc上传都是用 common-fileupload来实现 1.struts2上的方式需要在对应的Action,加上如下的属性以及get/set方法 private Fi ...
- jquery ajax和php实现返回值 json类型
js页面 $.ajax({ type: “POST”, dataType: ‘json’, url: “add_vote.php”, data: “touid=”+uid+”&touserna ...
- HDTunePro汉化版温度显示不正常后需要更改
查找:2564B046000000002564B043替换:2564A848000000002564A1E6 查找:B0432F2564B046替换:A1E62F2564A848
- React 源码剖析系列 - 不可思议的 react diff
简单点的重复利用已有的dom和其他REACT性能快的原理. key的作用和虚拟节点 目前,前端领域中 React 势头正盛,使用者众多却少有能够深入剖析内部实现机制和原理. 本系列文章希望通过剖析 ...
- TimeSpan格式化字符串格式(摘)
一直在用DateTime, 却不常用TimeSpan , 今天突然用到了, 发现不知道咋做格式化...百度一下,找到了答案, 在这记录一下, 免得以后找花费时间 以下内容摘抄自 Microsoft D ...
- vue2.*初体验
一. 推荐开发环境 二. 安装环境 安装 nvm :curl -o- https://raw.githubusercontent.com/creationix/nvm/v0.31.3/install. ...
- shell 脚本实战笔记(11)--Mysql在linux下的安装和简单运维
前言: linux中安装mysql以及配置的管理, 基础的运维和管理还是需要会一些的. 这边作下笔记, 以求天天向上(^_^). 安装流程:*). 安装mysql-server1). 借助yum检索相 ...
- 20155336 2016-2017-2《JAVA程序设计》第九周学习总结
20155336 2016-2017-2<JAVA程序设计>第九周学习总结 教材学习内容总结 第十六章 JDBC(Java DataBase Connectivity)即java数据库连接 ...
- 51Nod:1268 和为K的组合
1268 和为K的组合 基准时间限制:1 秒 空间限制:131072 KB 分值: 20 难度:3级算法题 收藏 关注 给出N个正整数组成的数组A,求能否从中选出若干个,使他们的和为K.如果可以 ...
- hdu2073-2078
hdu2073 数学 #include<stdio.h> #include<math.h> double len(double x){ )*(x+)); } int main( ...
