poj1066 Treasure Hunt【计算几何】

Treasure Hunt

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 8192		Accepted: 3376

Description

Archeologists from the Antiquities and Curios Museum (ACM) have flown to Egypt to examine the great pyramid of Key-Ops. Using state-of-the-art technology they are able to determine that the lower floor of the pyramid is constructed from a series of straightline walls, which intersect to form numerous enclosed chambers. Currently, no doors exist to allow access to any chamber. This state-of-the-art technology has also pinpointed the location of the treasure room. What these dedicated (and greedy) archeologists want to do is blast doors through the walls to get to the treasure room. However, to minimize the damage to the artwork in the intervening chambers (and stay under their government grant for dynamite) they want to blast through the minimum number of doors. For structural integrity purposes, doors should only be blasted at the midpoint of the wall of the room being entered. You are to write a program which determines this minimum number of doors. 
An example is shown below: 

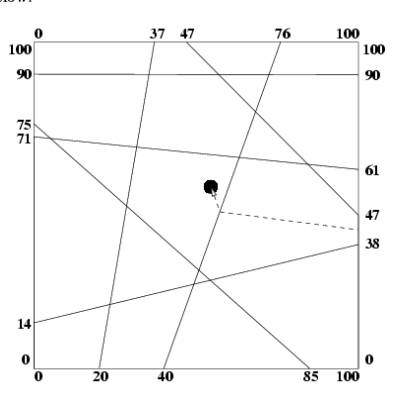
Input

The input will consist of one case. The first line will be an integer n (0 <= n <= 30) specifying number of interior walls, followed by n lines containing integer endpoints of each wall x1 y1 x2 y2 . The 4 enclosing walls of the pyramid have fixed endpoints at (0,0); (0,100); (100,100) and (100,0) and are not included in the list of walls. The interior walls always span from one exterior wall to another exterior wall and are arranged such that no more than two walls intersect at any point. You may assume that no two given walls coincide. After the listing of the interior walls there will be one final line containing the floating point coordinates of the treasure in the treasure room (guaranteed not to lie on a wall).

Output

Print a single line listing the minimum number of doors which need to be created, in the format shown below.

Sample Input

7
20 0 37 100
40 0 76 100
85 0 0 75
100 90 0 90
0 71 100 61
0 14 100 38
100 47 47 100
54.5 55.4 

Sample Output

Number of doors = 2 

Source

East Central North America 1999

题意：

一个正方形中有n面墙，告诉你一个宝藏所在的坐标。问最少要砸穿多少墙才能到达宝藏。

思路：

枚举宝藏坐标和所有的墙的端点构成一个线段。判断这个线段和多少墙相交，因为这个就是从某一个点进入的最短距离，相交的个数就是穿墙数。

这个端点就是最开始进入的点。

相当于那些墙的端点把外围墙划分成了很多区域，我们从某一个点进去。两个端点之间任何一个位置进去都是一样的，所以枚举端点就行了。

找一个最小值就行了。要注意有可能是从角进去的。

刚开始inter函数写错了。

 #include <iostream>
 #include <set>
 #include <cmath>
 #include <stdio.h>
 #include <cstring>
 #include <algorithm>
 #include <vector>
 #include <queue>
 #include <map>
 //#include <bits/stdc++.h>
 using namespace std;
 typedef long long LL;
 #define inf 0x7f7f7f7f

 const double eps = 1e-;
 int sgn(double x)
 {
     if(fabs(x) < eps)return ;
     if(x < )return -;
     else return ;
 }

 struct point{
     double x, y;
     point(){}
     point(double _x, double _y)
     {
         x = _x;
         y = _y;
     }
     point operator -(const point &b)const
     {
         return point(x - b.x, y - b.y);
     }
     point operator +(const point &b)const
     {
         return point(x + b.x, y + b.y);
     }
     point operator /(double d)const
     {
         return point(x / d, y / d);
     }
     double operator ^(const point &b)const
     {
         return x * b.y - y * b.x;
     }
     double operator *(const point &b)const
     {
         return x * b.x + y * b.y;
     }
     //绕原点旋转B
     void transXY(double b)
     {
         double tx = x, ty = y;
         x = tx * cos(b) - ty * sin(b);
         y = tx * sin(b) + ty * cos(b);
     }
 };
 struct line{
     point s, e;
     double k;
     line(){}
     line(point _s, point _e)
     {
         s = _s;
         e = _e;
         k = atan2(e.y - s.y, e.x - s.x);
     }
     pair<int, point>operator &(const line &b)const
     {
         point res = s;
         if(sgn((s - e) ^ (b.s - b.e)) == ){
             if(sgn((s - b.e) ^ (b.s - b.e)) == ){
                 return make_pair(, res);
             }
             else return make_pair(, res);
         }
         double t = ((s - b.s) ^ (b.s - b.e)) / ((s - e) ^ (b.s - b.e));
         res.x += (e.x - s.x) * t;
         res.y += (e.y - s.y) * t;
         return make_pair(, res);
     }
 };

 double dist(point a, point b)
 {
     return sqrt((a - b) * (a - b));
 }

 bool inter(line l1,line l2)
 {
     return
         max(l1.s.x,l1.e.x) >= min(l2.s.x,l2.e.x) &&
         max(l2.s.x,l2.e.x) >= min(l1.s.x,l1.e.x) &&
         max(l1.s.y,l1.e.y) >= min(l2.s.y,l2.e.y) &&
         max(l2.s.y,l2.e.y) >= min(l1.s.y,l1.e.y) &&
         sgn((l2.s-l1.s)^(l1.e-l1.s))*sgn((l2.e-l1.s)^(l1.e-l1.s)) <=  &&
         sgn((l1.s-l2.s)^(l2.e-l1.s))*sgn((l1.e-l2.s)^(l2.e-l2.s)) <= ;
 }

 const int maxn = ;
 line l[maxn];
 point treasure, p[maxn];
 int n;

 int main()
 {
     l[] = line(point(, ), point(, ));
     l[] = line(point(,), point(, ));
     l[] = line(point(, ), point(, ));
     l[] = line(point(, ), point(, ));
     while(scanf("%d", &n) != EOF){
         for(int i = ; i <= n + ; i++){
             scanf("%lf%lf%lf%lf", &l[i].s.x, &l[i].s.y, &l[i].e.x, &l[i].e.y);
             //[2 * i - 1] = l[i].s;
             //p[2 * i] = l[i].e;
         }
         scanf("%lf%lf", &treasure.x, &treasure.y);

         int ans = inf;
         for(int i = ; i <= ; i++){
             line l1 = line(treasure, l[i].s), l2 = line(treasure, l[i].e);
             int cnt1 = , cnt2 = ;
             for(int j = ; j <= n + ; j++){
                 if(inter(l1, l[j])){
                     cnt1++;
                     //cout<<cnt1<<endl;
                 }
                 if(inter(l2, l[j])){
                     cnt2++;
                     //cout<<cnt1<<endl;
                 }
             }
             ans = min(ans, cnt1 + );
             ans = min(ans, cnt2 + );
         }
         for(int i = ; i <= n + ; i++){
             line l1 = line(treasure, l[i].s), l2 = line(treasure, l[i].e);
             int cnt1 = , cnt2 = ;
             for(int j = ; j <= n + ; j++){
                 if(inter(l1, l[j])){
                     cnt1++;
                 }
                 if(inter(l2, l[j])){
                     cnt2++;
                 }
             }
             ans = min(ans, cnt1);
             ans = min(ans, cnt2);
         }
         /*for(int i = 1; i <= n * 2; i++){
             line l1 = line(treasure, p[i]);
             int cnt = 0;
             for(int j = 1; j <= n; j++){
                 if(inter(l1, l[j])){
                     cnt++;
                 }
             }
             ans = min(ans, cnt);
             //cout<<ans<<endl;
         }
         line l1 = line(treasure, point(0, 0));
         int cnt = 0;
         for(int i = 1; i <= n; i++){
             if(inter(l1, l[i])){
                 cnt++;
             }
         }
         ans = min(ans, cnt + 1);
         cnt = 0;
         l1 = line(treasure, point(0, 100));
         for(int i = 1; i <= n; i++){
             if(inter(l1, l[i])){
                 cnt++;
             }
         }
         ans = min(ans, cnt + 1);
         cnt = 0;
         l1 = line(treasure, point(100, 0));
         for(int i = 1; i <= n; i++){
             if(inter(l1, l[i])){
                 cnt++;
             }
         }
         ans = min(ans, cnt + 1);
         cnt = 0;
         l1 = line(treasure, point(100, 100));
         for(int i = 1; i <= n; i++){
             if(inter(l1, l[i])){
                 cnt++;
             }
         }
         ans = min(ans, cnt + 1);*/
         printf("Number of doors = %d\n", ans);
     }
     return ;
 }