P3195 [HNOI2008]玩具装箱TOY（斜率优化dp）

P3195 [HNOI2008]玩具装箱TOY

设前缀和为$s[i]$

那么显然可以得出方程

$f[i]=f[j]+(s[i]-s[j]+i-j-L-1)^{2}$

换下顺序

$f[i]=f[j]+(s[i]+i-(s[j]+j+L+1))^{2}$

为了处理方便，我们套路地设

$a[i]=s[i]+i$

$b[i]=s[i]+i+L+1$

于是得出

$f[i]=f[j]+(a[i]-b[j])^{2}$

拆开：$f[i]=f[j]+a[i]^{2}-2*a[i]*b[j]+b[j]^{2}$

移项：$f[j]+b[j]^{2}=2*a[i]*b[j]+f[i]-a[i]^2$

于是我们就把不变量和变量分开了（$i$固定）

仔细观察

$f[j]+b[j]^{2}=2*a[i]*b[j]+f[i]-a[i]^2$

$y=k*x+b$

一次函数！

$y=f[j]+b[j]^{2}$

$k=2*a[i]$（$i$递增时，显然它是单调递增的）

$x=b[j]$

$b=f[i]-a[i]^{2}$

如果我们要让$f[i]$最小，就是让$b$最小

而对于每个$i$，$k$是不变的

那么问题就转化成：找到一个最优的$(x,y)$使$b$最小

考虑到$k$是单调递增的

于是我们就可以快乐地用单调队列维护下凸包辣

while(L<R&&K(h[L],h[L+])<=*a(i)) ++L;//显然h[L]不比h[L+1]优，可以删去
f[i]=f[h[L]]+(a(i)-b(h[L]))*(a(i)-b(h[L]));//计算出最优的f[i]
while(L<R&&K(h[R-],h[R])>K(h[R],i)) --R;//加入点（x[i],y[i]）后，h[R]在凸包内部，可以删去①
h[++R]=i;//入队

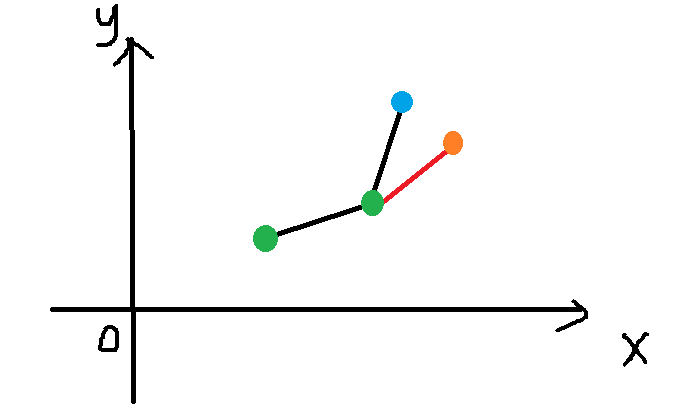
①：显然在加入橙点后，蓝点在凸包内部，可以被删除

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
typedef double db;
#define N 50005
db f[N],s[N];
int n,l,L,R,h[N];
inline db a(int x){return s[x]+x;}
inline db b(int x){return s[x]+x+l+;}
inline db X(int x){return b(x);}
inline db Y(int x){return f[x]+b(x)*b(x);}
inline db K(int x,int y){return (Y(x)-Y(y))/(X(x)-X(y));}
int main(){
    scanf("%d%d",&n,&l);
    for(int i=;i<=n;++i) scanf("%lf",&s[i]),s[i]+=s[i-];
    L=R=;
    for(int i=;i<=n;++i){
        while(L<R&&K(h[L],h[L+])<=*a(i)) ++L;
        f[i]=f[h[L]]+(a(i)-b(h[L]))*(a(i)-b(h[L]));
        while(L<R&&K(h[R-],h[R])>K(h[R],i)) --R;
        h[++R]=i;
    }printf("%.0lf",f[n]);
    return ;
}