深入理解L1、L2正则化

过节福利，我们来深入理解下L1与L2正则化。

1 正则化的概念

• 正则化(Regularization) 是机器学习中对原始损失函数引入额外信息，以便防止过拟合和提高模型泛化性能的一类方法的统称。也就是目标函数变成了原始损失函数+额外项，常用的额外项一般有两种，英文称作\(ℓ1-norm\)和\(ℓ2-norm\)，中文称作L1正则化和L2正则化，或者L1范数和L2范数（实际是L2范数的平方）。

• L1正则化和L2正则化可以看做是损失函数的惩罚项。所谓惩罚是指对损失函数中的某些参数做一些限制。对于线性回归模型，使用L1正则化的模型叫做Lasso回归，使用L2正则化的模型叫做Ridge回归（岭回归）。

• 线性回归L1正则化损失函数：
  \[\min_w [\sum_{i=1}^{N}(w^Tx_i - y_i)^2 + \lambda \|w\|_1 ]........(1)\]

• 线性回归L2正则化损失函数：
  \[\min_w[\sum_{i=1}^{N}(w^Tx_i - y_i)^2 + \lambda\|w\|_2^2] ........(2)\]

• 公式(1)(2)中\(w\)表示特征的系数（\(x\)的参数），可以看到正则化项是对系数做了限制。L1正则化和L2正则化的说明如下：
  • L1正则化是指权值向量\(w\)中各个元素的绝对值之和，通常表示为\(\|w\|_1\)。
  • L2正则化是指权值向量\(w\)中各个元素的平方和然后再求平方根（可以看到Ridge回归的L2正则化项有平方符号），通常表示为\(\|w\|_2^2\)。
  • 一般都会在正则化项之前添加一个系数\(\lambda\)。Python中用\(\alpha\)表示，这个系数需要用户指定（也就是我们要调的超参）。

2 正则化的作用

• L1正则化可以使得参数稀疏化，即得到的参数是一个稀疏矩阵，可以用于特征选择。
  • 稀疏性，说白了就是模型的很多参数是0。通常机器学习中特征数量很多，例如文本处理时，如果将一个词组（term）作为一个特征，那么特征数量会达到上万个（bigram）。在预测或分类时，那么多特征显然难以选择，但是如果代入这些特征得到的模型是一个稀疏模型，很多参数是0，表示只有少数特征对这个模型有贡献，绝大部分特征是没有贡献的，即使去掉对模型也没有什么影响，此时我们就可以只关注系数是非零值的特征。这相当于对模型进行了一次特征选择，只留下一些比较重要的特征，提高模型的泛化能力，降低过拟合的可能。
• L2正则化可以防止模型过拟合（overfitting）；一定程度上，L1也可以防止过拟合。

3 L1正则化与稀疏性

• 事实上，”带正则项”和“带约束条件”是等价的。

• 为了约束w的可能取值空间从而防止过拟合，我们为该最优化问题加上一个约束，就是w的L1范数不能大于m：
  \[
  \begin{cases}
  \min \sum_{i=1}^{N}(w^Tx_i - y_i)^2 \\
  s.t. \|w\|_1 \leqslant m.
  \end{cases}........(3)
  \]

• 问题转化成了带约束条件的凸优化问题，写出拉格朗日函数:
  \[ \sum_{i=1}^{N}(w^Tx_i - y_i)^2 + \lambda (\|w\|_1-m)........(4)\]

• 设\(W_*\)和\(\lambda_*\)是原问题的最优解，则根据\(KKT\)条件得：
  \[
  \begin{cases}
  0 = \nabla_w[\sum_{i=1}^{N}(W_*^Tx_i - y_i)^2 + \lambda_* (\|w\|_1-m)] \\
  0 \leqslant \lambda_*.
  \end{cases}........(5)
  \]

• 仔细看上面第一个式子，与公式(1)其实是等价的，等价于(3)式。
• 设L1正则化损失函数：\(J = J_0 + \lambda \sum_{w} |w|\)，其中\(J_0 = \sum_{i=1}^{N}(w^Tx_i - y_i)^2\)是原始损失函数，加号后面的一项是L1正则化项，\(\lambda\)是正则化系数。
• 注意到L1正则化是权值的绝对值之和，\(J\)是带有绝对值符号的函数，因此\(J\)是不完全可微的。机器学习的任务就是要通过一些方法（比如梯度下降）求出损失函数的最小值。当我们在原始损失函数\(J_0\)后添加L1正则化项时，相当于对\(J_0\)做了一个约束。令\(L=\lambda \sum_w|w|\)，则\(J=J_0+L\)，此时我们的任务变成在\(L\)约束下求出\(J_0\)取最小值的解。
• 考虑二维的情况，即只有两个权值\(w_1\)和\(w_2\)，此时\(L=|w_1|+|w_2|\)对于梯度下降法，求解\(J_0\)的过程可以画出等值线，同时L1正则化的函数\(L\)也可以在\(w_1\)、\(w_2\)的二维平面上画出来。如下图：
  
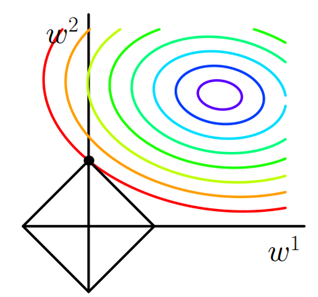
• 上图中等值线是\(J_0\)的等值线，黑色方形是\(L\)函数的图形。在图中，当\(J_0\)等值线与\(L\)图形首次相交的地方就是最优解。上图中\(J_0\)与\(L\)在\(L\)的一个顶点处相交，这个顶点就是最优解。注意到这个顶点的值是\((w_1,w_2)=(0,w_2)\)。可以直观想象，因为\(L\)函数有很多突出的角（二维情况下四个，多维情况下更多），\(J_0\)与这些角接触的机率会远大于与\(L\)其它部位接触的机率，而在这些角上，会有很多权值等于\(0\)，这就是为什么L1正则化可以产生稀疏模型，进而可以用于特征选择。

• 而正则化前面的系数\(\lambda\)，可以控制\(L\)图形的大小。\(\lambda\)越小，\(L\)的图形越大（上图中的黑色方框)；\(\lambda\) 越大，\(L\)的图形就越小，可以小到黑色方框只超出原点范围一点点，这是最优点的值\((w_1,w_2)=(0,w_2)\)中的\(w_2\)可以取到很小的值。

• 同理，又L2正则化损失函数：\(J = J_0 + \lambda \sum_w w^2\),同样可画出其在二维平面的图像，如下：
  

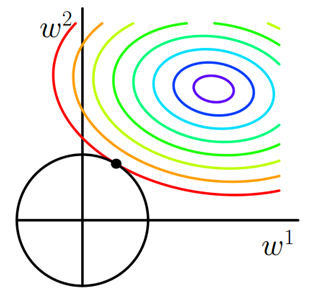
• 二维平面下L2正则化的函数图形是个圆，与方形相比，被磨去了棱角。因此\(J_0\)与\(L\)相交时使得\(w_1\)或\(w_2\)等于零的机率小了许多，这就是为什么L2正则化不具有稀疏性的原因。

4 L2正则化为什么能防止过拟合

• 拟合过程中通常都倾向于让权值尽可能小，最后构造一个所有参数都比较小的模型。因为一般认为参数值小的模型比较简单，能适应不同的数据集，也在一定程度上避免了过拟合现象。可以设想一下对于一个线性回归方程，若参数很大，那么只要数据偏移一点点，就会对结果造成很大的影响；但如果参数足够小，数据偏移得多一点也不会对结果造成什么影响，专业一点的说法是抗扰动能力强。
• 为什么L2正则化可以获得值很小的参数?
• (1) 以线性回归中的梯度下降法为例。假设要求的参数为\(\theta\)，\(h \theta (x)\)是我们的假设函数，那么线性回归的代价函数如下：
  \[ J_{\theta} = \frac{1}{2n}\sum_{i=1}^n (h \theta (x^{(i)}) - y^{(i)})^2 ........(6)\]
• (2)在梯度下降中\(\theta\)的迭代公式为：
  \[\theta_j = \theta_j - \alpha \frac{1}{n} \sum_{i=1}^n (h \theta (x^{(i)}) - y^{(i)}) x_j^{(i)}........(7)\]
• (3) 其中\(\alpha\)是learning rate。 上式是没有添加L2正则化项的迭代公式，如果在原始代价函数之后添加L2正则化，则迭代公式为：
  \[\theta_j = \theta_j(1- \alpha \frac{\lambda}{n}) - \alpha \frac{1}{n} \sum_{i=1}^n (h \theta (x^{(i)}) - y^{(i)}) x_j^{(i)} ........(8)\]
• 其中\(\lambda\)就是正则化参数。从上式可以看到，与未添加L2正则化的迭代公式相比，每一次迭代，\(\theta_j\)都要先乘以一个小于1的因子，从而使得\(\theta_j\)不断减小，因此总得来看，\(\theta\)是不断减小的。
  最开始也提到L1正则化一定程度上也可以防止过拟合。之前做了解释，当L1的正则化系数很小时，得到的最优解会很小，可以达到和L2正则化类似的效果。

5 正则化项的参数选择

• L1、L2的参数\(\lambda\)如何选择好?
• 以L2正则化参数为例：从公式(8)可以看到，λ越大，\(\theta_j\)衰减得越快。另一个理解可以参考L2求解图， \(\lambda\)越大，L2圆的半径越小，最后求得代价函数最值时各参数也会变得很小；当然也不是越大越好，太大容易引起欠拟合。
• 经验
  从0开始，逐渐增大\(\lambda\)。在训练集上学习到参数，然后在测试集上验证误差。反复进行这个过程，直到测试集上的误差最小。一般的说，随着\(\lambda\)从0开始增大，测试集的误分类率应该是先减小后增大，交叉验证的目的，就是为了找到误分类率最小的那个位置。建议一开始将正则项系数λ设置为0，先确定一个比较好的learning rate。然后固定该learning rate，给\(\lambda\)一个值（比如1.0），然后根据validation accuracy，将λ增大或者减小10倍，增减10倍是粗调节，当你确定了\(\lambda\)的合适的数量级后，比如\(\lambda= 0.01\)，再进一步地细调节，比如调节为0.02，0.03，0.009之类。

参考文献

• https://blog.csdn.net/jinping_shi/article/details/52433975
• 《百面机器学习》