2018.4.23-ml笔记(线性回归、梯度下降)
线性回归:找到最合适的一条线来最好的拟合我们的数据点。
hθ(x) = θixi=θTx θ被称之为权重参数 θ0为拟合参数
对每个样本yi=θTxi + εi 误差ε是独立并且具有相同的分布,并且服从均值为0且方差为θ2的高斯分布。
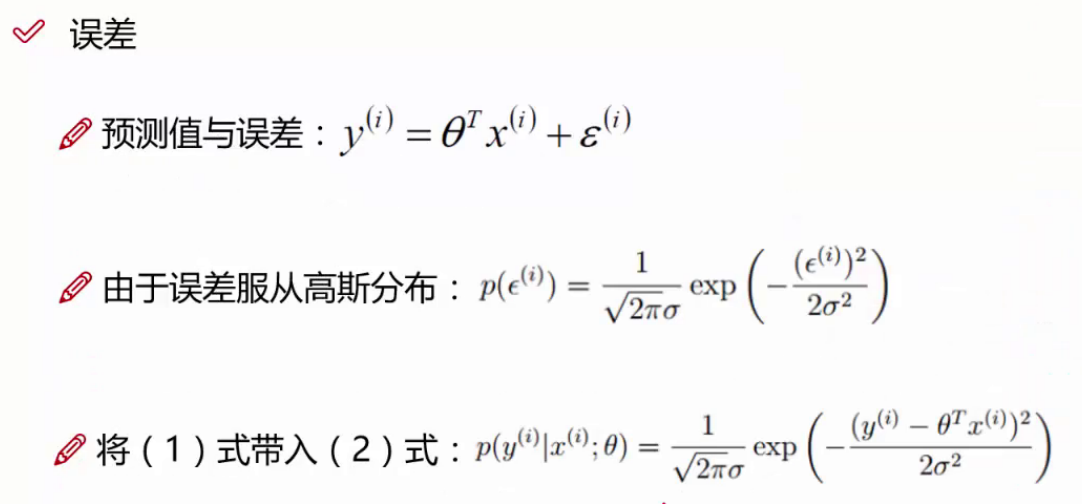


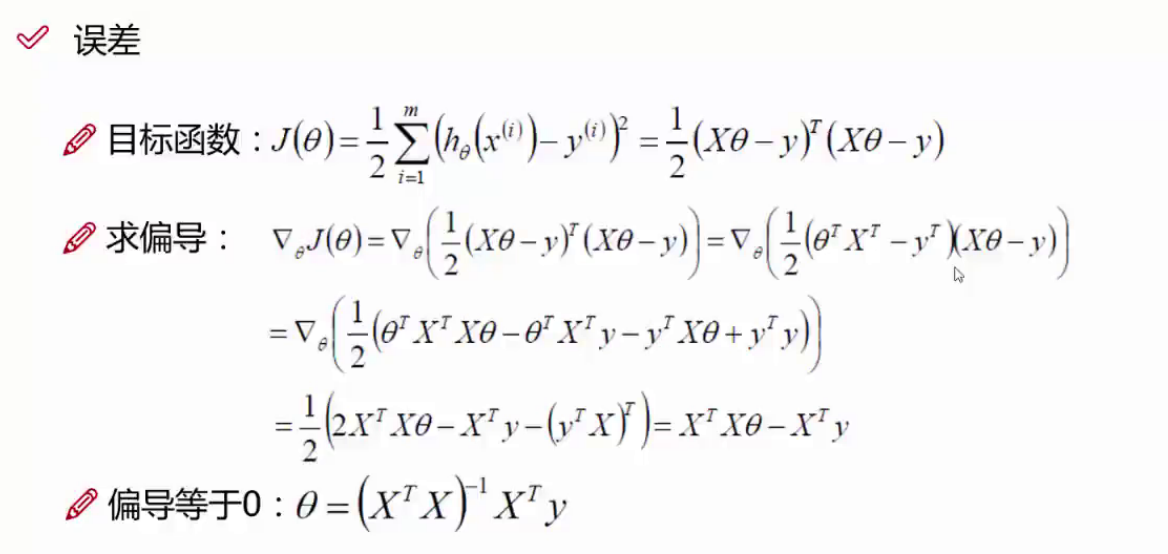




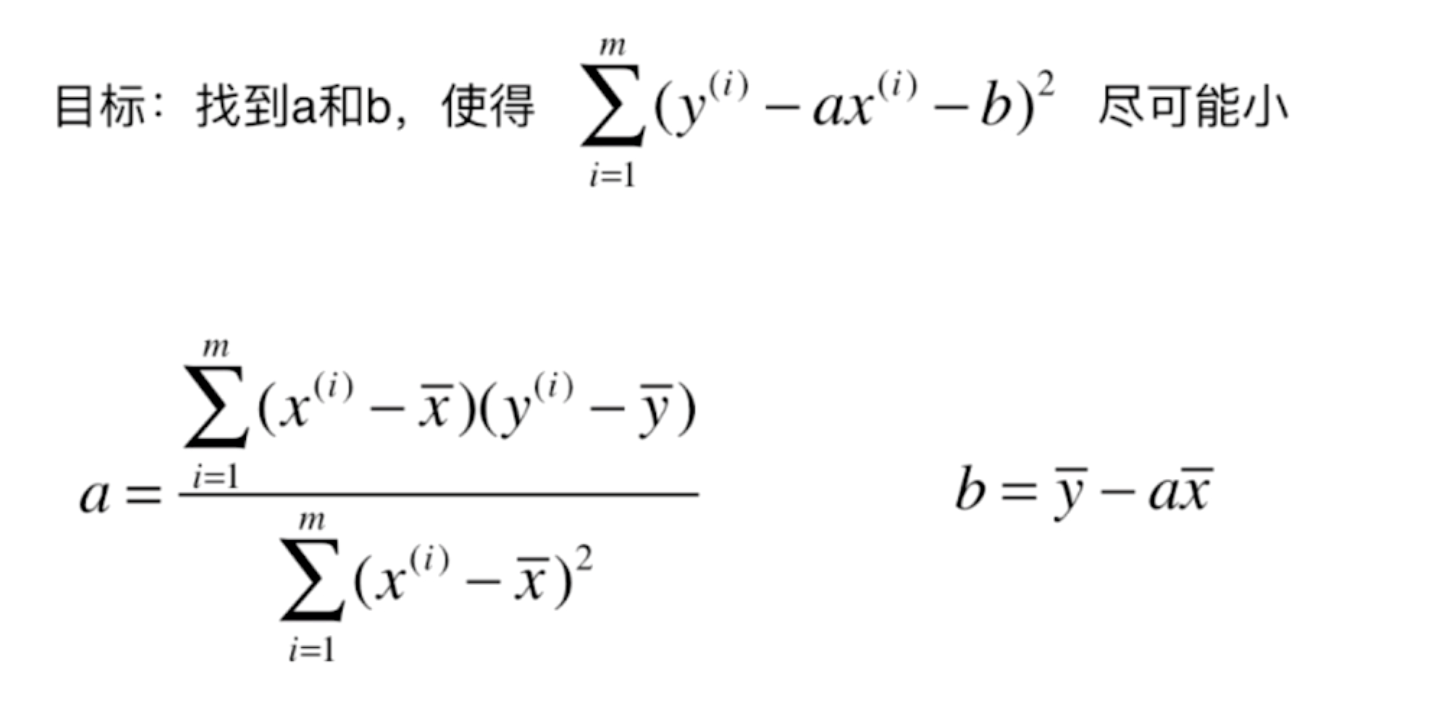
2018.4.23-ml笔记(线性回归、梯度下降)的更多相关文章
- [笔记]线性回归&梯度下降
一.总述 线性回归算法属于监督学习的一种,主要用于模型为连续函数的数值预测. 过程总得来说就是初步建模后,通过训练集合确定模型参数,得到最终预测函数,此时输入自变量即可得到预测值. 二.基本过程 1. ...
- 线性回归 Linear regression(2)线性回归梯度下降中学习率的讨论
这篇博客针对的AndrewNg在公开课中未讲到的,线性回归梯度下降的学习率进行讨论,并且结合例子讨论梯度下降初值的问题. 线性回归梯度下降中的学习率 上一篇博客中我们推导了线性回归,并且用梯度下降来求 ...
- 大叔学ML第一:梯度下降
目录 原理 实践一:求\(y = x^2 - 4x + 1\)的最小值 实践二:求\(z = x^2 + y^2 + 5\)的最小值 问答时间 原理 梯度下降是一个很常见的通过迭代求解函数极值的方法, ...
- 机器学习(1)之梯度下降(gradient descent)
机器学习(1)之梯度下降(gradient descent) 题记:最近零碎的时间都在学习Andrew Ng的machine learning,因此就有了这些笔记. 梯度下降是线性回归的一种(Line ...
- Python实现——一元线性回归(梯度下降法)
2019/3/25 一元线性回归--梯度下降/最小二乘法_又名:一两位小数点的悲剧_ 感觉这个才是真正的重头戏,毕竟前两者都是更倾向于直接使用公式,而不是让计算机一步步去接近真相,而这个梯度下降就不一 ...
- ng机器学习视频笔记(一)——线性回归、代价函数、梯度下降基础
ng机器学习视频笔记(一) --线性回归.代价函数.梯度下降基础 (转载请附上本文链接--linhxx) 一.线性回归 线性回归是监督学习中的重要算法,其主要目的在于用一个函数表示一组数据,其中横轴是 ...
- 斯坦福机器学习视频笔记 Week1 线性回归和梯度下降 Linear Regression and Gradient Descent
最近开始学习Coursera上的斯坦福机器学习视频,我是刚刚接触机器学习,对此比较感兴趣:准备将我的学习笔记写下来, 作为我每天学习的签到吧,也希望和各位朋友交流学习. 这一系列的博客,我会不定期的更 ...
- Andrew Ng机器学习公开课笔记 -- 线性回归和梯度下降
网易公开课,监督学习应用.梯度下降 notes,http://cs229.stanford.edu/notes/cs229-notes1.pdf 线性回归(Linear Regression) 先看个 ...
- 吴恩达机器学习笔记7-梯度下降III(Gradient descent intuition) --梯度下降的线性回归
梯度下降算法和线性回归算法比较如图: 对我们之前的线性回归问题运用梯度下降法,关键在于求出代价函数的导数,即: 我们刚刚使用的算法,有时也称为批量梯度下降.实际上,在机器学习中,通常不太会给算法起名字 ...
- ML(附录1)——梯度下降
梯度下降是迭代法的一种,可以用于求解最小二乘问题(线性和非线性都可以).在求解机器学习算法的模型参数,即无约束优化问题时,梯度下降(Gradient Descent)是最常采用的方法之一,另一种常用的 ...
随机推荐
- [leetcode]38. Count and Say数数
The count-and-say sequence is the sequence of integers with the first five terms as following: 1. 1 ...
- 根据需要查找需要的第三方pyhton库
1.可以在https://awesome-python.com/这个网站上按照分类去寻找,上面收录了比较全面的第三方库.比如我们想要找爬虫方面的库时,查看Web Crawling这个分类,就能看到相应 ...
- jsp相关笔记(一)
1.在html中调整两个<p>标签之间的间距,可以用margin属性: p { margin: 0.2em 0;} 2.在jsp中要对页面分成上.左.右三栏时,可以用<framese ...
- 代码之髓读后感——类&继承
面向对象 语言中的用语并不是共通的,在不同语言中,同一个用语的含义可能会有很大差别. C++的设计者本贾尼·斯特劳斯特卢普对类和继承给予了正面肯定,然而,"面向对象"这个词的发明者 ...
- AX_NumberSeq
NumberSeq::newGetNum(NumberSeqReference::findReference(typeId2ExtendedTypeId(typeid(InventTransId))) ...
- Spring的介绍与搭建
一.Spring的介绍 二.Spring的搭建 (1)导包 (2)创建一个对象 (3)书写配置注册对象到容器 (4)代码测试
- SignalR 服务器系统配置要求
SignalR 所支持的服务器版本..NET Framework 版本.IIS和其他组件. SignalR操作系统要求 SignalR组件能够运行在下面的服务器和客户端操作系统.需要注意的是使用Web ...
- docker学习笔记-命令大全
容器生命周期管理 • Run OPTIONS说明: • -a :显示所有的容器,包括未运行的. • -f :根据条件过滤显示的内容. • --format :指定返回值的模板文件. • -l :显示最 ...
- verilog 有符号数运算
1)之前的笔记写过<补码探讨>,可知在FPGA综合成电路的时候最底层都是以补码的形式在运算,正数的补码就是本身,负数的补码要取反+1. (2)那么Verilog中编程的时候对编程人员来说, ...
- ubuntu上vsftpd服务配置
Ubuntu上提供两种常用的ftp服务应用:vsftpd 和 tftpd,区别如下: 1)vsftpd 支持客户端上下传文件,支持浏览器显示及下载,支持用户名密码认证,支持匿名访问,默认端口TCP:2 ...
