浅谈AC自动机

写在前面：从10月23日开始写这篇博文，离NOIP2018只有十多天了。坚持不停课的倔强蒟蒻（我）尽量每天挤时间多搞一搞信竞（然而还要准备期中考试）。NOIP争取考一个好成绩吧。

一、简介

AC自动机，全称Aho-Corasick automaton，该算法在1975年产生于贝尔实验室，是著名的多模匹配算法。（并不是让你的代码自动AC的算法）

AC自动机是必须建立在KMP和Trie的基础上的。所以如果你不会KMP或Trie，你可以给这篇文章点赞然后去看：

KMP

Trie

我们知道，KMP算法是处理一个字符串（模式串）对应一段文本（主串）的，而AC自动机是用来处理多个字符串和一段文本的匹配问题的

举个例子：

有N个单词，平均长度为L；文章长度为M。求这些单词在文中出现了多少次？（一个单词出现多次算多次）

Algorithm1：暴力。时间复杂度O(NML)

Algorithm2：AC自动机。时间复杂度O((N+M)L)

二、步骤

简单来说分为三步：

1、将所有的单词（模式串）构建一棵Trie

2、构造每一个结点的nxt数组

3、利用前缀指针对文本进行匹配

这里的前缀指针是算法的重点，与KMP中的next数组十分相似。所以AC自动机可以看作是在Trie上的KMP。

三、详细流程

（一）将所有的单词（模式串）构建一棵Trie

这个Trie跟普通的Trie没有任何区别，不做讲解了

注意一点，如果本题的要求是一个单词出现多次算做多次的话，那么Trie中的book数组每遍要+1而不是=1

（二）构造每一个结点的nxt数组

这个重点讲解一下

首先假设我们的Trie长这个样子：

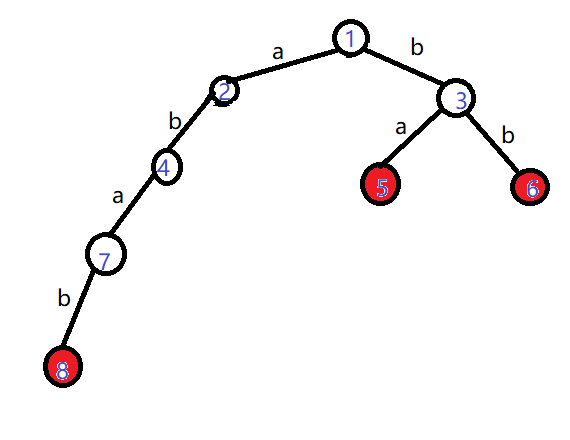
需要匹配的文本是"abb"

我们前两个字符都能匹配：

我们走到了4号结点。

然后我们发现下一个字符是'b'，然而四号节点的儿子中没有4！

那该怎么办呢？

要返回根节点并从'b'继续搜索吗？

不能这么做！因为如果这样，前两个字符'ab'不就浪费掉了吗？而我们的目的是找到全部的单词啊。

所以就会想到，对于前两个字符，我们要尽可能的保留

“尽可能地保留”换成严谨的语言就是满足最长后缀关系

即：在Trie上另找一个结点，使它所代表的字符串与当前节点所代表的字符串拥有最长的公共后缀

在上面的例子中，我们找到3号节点。它所代表的字符串是'b'，与当前字符串'ab'具有最长的公共后缀

那就是它了！

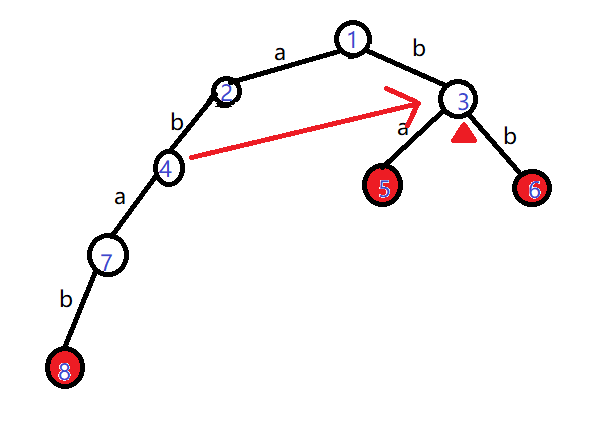
继续查找。文本中的第三个字符是'b'，而3号结点的儿子中有'b'，还恰好有book标记。

那么我们就找到了一个单词'bb'！

思考上面的过程，有没有觉得上图中的那个红色箭头非常重要？在我们匹配失败时，它可以告诉我们一个新的结点并继续匹配。

我们还发现，每个结点的“失配箭头”都是固定的，只与模式串有关，与主串（文本）无关！

那么，完全可以预处理出一个数组，将每个结点的“失配箭头”储存下来！

艾玛……厉害了

这个数组，就是AC自动机中的核心，nxt数组！

nxt[i]=j表示当匹配到i无法匹配时，j所代表的字符串与i所代表的字符串拥有最长公共后缀，所以接下来就要到j继续匹配

说的这么多，终于把nxt数组是什么以及它的用途说完了……不知道说清楚没有

下面是某个Trie的nxt数组建立过程（图片来自于《信息学奥赛一本通.提高篇》）

换成代码就是这样的：

for(i=;i<;i++)
        if(trie[][i])
            Q.push(trie[][i]);
    while(!Q.empty())
    {
        int u=Q.front();
        Q.pop();
        for(i=;i<;i++)
        {
            if(trie[u][i])
            {
                f[trie[u][i]]=trie[f[u]][i];
                Q.push(trie[u][i]);
            }
            else trie[u][i]=trie[f[u]][i];//优化
        }
    }
    return ;
}

上面代码中的else那个优化是怎么回事呢？

实际情况中，若不存在trie[u][i]的转移边，那么就需要一直让u=f[u]直到找到一个有i的转移边的点，设该点为点v。那我们就直接让trie[u][i]=trie[v][i]（也就是trie[u][i]=trie[f[u]][i]）。

也正是因为如此，存在trie[u][i]的转移边时并不需要考虑trie[f[u]][i]的转移边不存在的情况（就算不存在，以前肯定也处理好了），直接赋值就OK了。这样不仅代码好写，而且优化了时间。

（三）匹配

接着输入一段文本，对着处理好nxt数组的trie进行匹配就可以了

详见代码：

void get_ans(char *a)
{
    int u=,len=strlen(a);
    for(i=;i<len;i++)//枚举主串每一个字符
    {
        int c=a[i]-'a';
        u=trie[u][c];
        for(int k=u;k && book[k]!=-;k=f[k])//统计所有以字符c结尾的单词
            ans+=book[k],book[k]=-;//book置为-1，避免重复统计
    }
}

差不多就讲完了

学之前觉得AC自动机是个高大上的东西，但其实搞懂之后就很奇妙了

板子：

洛谷P3808

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<queue>
using namespace std;

inline int read()
{
    int f=,x=;
    char ch=getchar();
    while(ch<'' || ch>'') {if(ch=='-') f=-; ch=getchar();}
    while(ch>='' && ch<='') {x=x*+ch-''; ch=getchar();}
    return x*f;
}

int n,cnt,ans;
int trie[][],book[],f[];
int i;
queue <int> Q;

void build(char *a)
{
    int u=,len=strlen(a);
    for(i=;i<len;i++)
    {
        int c=a[i]-'a';
        if(!trie[u][c])
            trie[u][c]=++cnt;
        u=trie[u][c];
    }
    book[u]++;
    return ;
}

void bfs()
{
    for(i=;i<;i++)
        if(trie[][i])
            Q.push(trie[][i]);
    while(!Q.empty())
    {
        int u=Q.front();
        Q.pop();
        for(i=;i<;i++)
        {
            if(trie[u][i])
            {
                f[trie[u][i]]=trie[f[u]][i];
                Q.push(trie[u][i]);
            }
            else trie[u][i]=trie[f[u]][i];
        }
    }
    return ;
}

void get_ans(char *a)
{
    int u=,len=strlen(a);
    for(i=;i<len;i++)
    {
        int c=a[i]-'a';
        u=trie[u][c];
        for(int k=u;k && book[k]!=-;k=f[k])
            ans+=book[k],book[k]=-;
    }
}

int main()
{
    n=read();
    char a[];
    for(int k=;k<=n;k++)
    {
        scanf("%s",a);
        build(a);
    }
    bfs();
    scanf("%s",a);
    get_ans(a);
    printf("%d",ans);
    return ;
}

AC代码（仅供参考）

本文部分内容参考《信息学奥赛一本通.提高篇》第二部分第四章 AC自动机

若需转载，请注明https://www.cnblogs.com/llllllpppppp/p/9839718.html

~NOIP2018 加油~