细讲递归（recursion）

入门

首先先对递归进行入门。

递归是以自相似的方式重复项目的过程。在编程语言中，如果程序允许您在同一函数内调用函数，则称其为函数的递归调用。

简而言之，递归就是函数的自身调用。可以看看下面的递归使用：

void Recursive() {
    Recursive();//call itself
}

int main(void)
{
    Recursive();

    system("PAUSE");
    return ;
}

借前辈一句话，递归定义就是：递归中的“递”就是入栈，递进；“归”就是出栈，回归。

因为递归在整个函数结束时才释放数据区，而每一次调用函数都会存储临时的变量，因此递归次数过多，会造成栈溢出，上面的例子就会出现这种状况。

如果你会将递归与return联系起来，但实际上return的作用只是将值返回给调用参数的函数。

N项求和

我们以前都计算过求1+2+3+4+...+n，n项求和。现在要求我们使用递归写出来。

1.我们设第n项的和为sum(n)，而前n项之和，可以由前n-1项之和加第n项。用表达式就是:sum(n-1) + n。

可以得到关系式:sum(n) = sum(n -1) + n;

2.接下来我们可以想一下，sum(n-1)又等于前一项加n-1一直循环下去计算，直到sum(2) = sum(1) + 2;计算完毕，此时sum(2)是我们要求的值，sum(1)是未知的，因此我们还需要知道sum(1)的值,才能求前n项和。

由1， 2的叙述，我们列出：

sum(n) = sum(n-) + n;
sum() = ;

我们将第一个式子称作为“关系”， 第二个式子称作“出口”（可以理解为结束递归的条件）。

由此我们可以写出程序：

#include <stdio.h>
#include <stdlib.h>

int sum(int n) {
    if (n == ) {
        return ;
    }
    else {
        return sum(n - ) + n;
    }
}

int main(void)
{
    int k = sum();

    printf("%d\n", k);

    system("PAUSE");
    return ;
}

Question:

接着我们可以试着自己做一下n!的递归计算，同样是第n项等于 前n-1项相乘 *  第n项，出口为第1项，当然出口也可以为第m项(m>0&&m<=n)，但我们这里算n!，就不管了。

奇/偶数求和

同样，对于奇数，偶数求和也就是前n项的变型，这里不再说，我们这里可以对奇/偶数求第n项的值，进行递归计算。这里举例奇数计算：1+3+5+7...，设num(n)为第n个奇数。

1.通过第一个例子我们首先可以列出关系，num(n) = num(n - 1) + 2;

2.写出出口，num(1) = 1;

写出主要程序：

int num(int n) {
    if (n == ) {
        return ;
    }
    else {
        return num(n - ) + ;
    }
}

斐波那契数列(Fibonacci sequence)

接着我们看看 斐波那契数列：1, 1, 2, 3, 5, 8, 13...

得出规律，后一项等于前两项相加。写出关系式f(n) = f(n-1) + f(n-2);

随之我们对关系式的出口（结束条件）进行判断，我们需要求f(n)，而f(n-1)和f(n-2)都是未知的，我们只写其中一项为出口都是不够的，因此我们需要两个出口。f(1) = 1; f(2) = 1;

通过关系和出口，我们写出：

f(n) = f(n-) + f(n-);
f() = ;
f() = ;

写出程序：

#include <stdio.h>
#include <stdlib.h>

int f(int n) {
    if (n == ) return ;
    if (n == ) return ;

    return f(n - ) + f(n - );
}

int main(void)
{
    int k = f();

    printf("%d\n", k);

    system("PAUSE");
    return ;
}

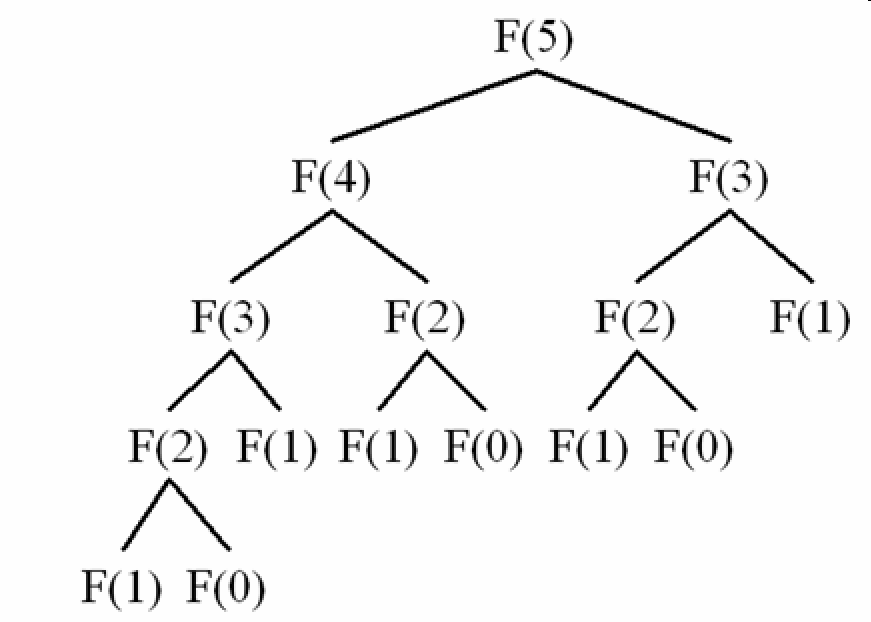
可以发现越高层的函数调用，自身调用的次数越多。

数组求和

使用递归，对数组array[] = { 1, 2, 3, 4, 5, 6};求和。

和之前n项求和思想相似，不过这里多了将数组地址传入，同样我们可以将数组关系写出 sum(array, n) = sum(array, n-1) + array[n];   注意：我们这里传入的n应当是数组的最大下标（数组从0~n-1,n个数）。

很显然作为递归出口的应当是当数组下标为0时，sum(array, 0) = array[0];

我们可以写出程序：

#include <stdio.h>
#include <stdlib.h>

int sum(int *arr, int n) {
    if (n == ) return arr[];

    return sum(arr, n - ) + arr[n];
}

int main(void)
{
    int array[] = { , , , , ,  };
    int k = sum(array, sizeof(array) / sizeof(int) - );//这里填数组最大下标
    //int k = sum(array, 5);
    printf("数组元素之和:%d", k);
    system("PAUSE");
    return ;
}

汉诺塔问题

有三根杆子A，B，C。A杆上有N个(N>1)穿孔圆环，盘的尺寸由下到上依次变小。要求按下列规则将所有圆盘移至C杆：

1. 每次只能移动一个圆盘；
2. 大盘不能叠在小盘上面。

这道题的解题步骤就三个：

1. 将A(source)杆中前n - 1个盘移到B(auxiliary)杆；
2. 将A(source)杆最后一个盘移到C(destination)杆；
3. 将B(auxiliary)杆n - 1个盘移到C(destination)杆；

动态图演示（借前辈图一用）

如果这样说你还是不能理解过程，那么我们就回想一下之前的n项求和，我们将前n-1项 + 第n项。那么在这里，我们将前n-1个盘看成一个整体(盘的位置不变），将最后一个大盘看成一个整体，先将那一大坨移到B杆，再把A杆剩下的那个大盘移到C杆，然后我们再把那一大坨移到C杆。

整体过程：

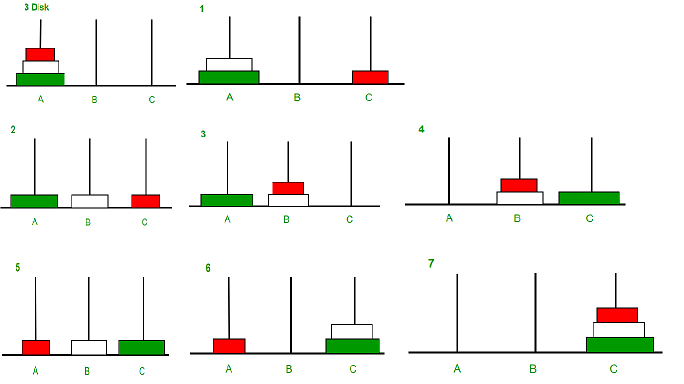
 a.同样的这道题我们通过解题步骤去找关系式：(整个函数的声明是void Hanoi(int n, char SourcePole, char AuxiliaryPole, char DestinationPole);)

1. Hanoi(n - 1,  SourcePole, DestinationPole, AuxiliaryPole);
2. printf("将盘%d,从%c柱------>%c柱\n", n ,SourcePole, DestinationPole);
3. Hanoi(n - 1,  AuxiliaryPole, SourcePole, DestinationPole);

(因为输出对象是SourcePole到DestinationPole,因此我们要将A杆的盘转移到B杆上，就需要在递归调用函数，传入参数时，将参数换位。)

b.接着我们写出口，移动n - 1个盘，也就是1~（n -1）,当n = 0时结束函数。

因此写出程序：

#include <stdio.h>
#include <stdlib.h>

void Hanoi(int n, char SourcePole, char AuxiliaryPole, char DestinationPole){
    if(n == ){
        return;
    }
    Hanoi(n - , SourcePole, DestinationPole, AuxiliaryPole);
    printf("将盘%d,从%c柱------>%c柱\n", n ,SourcePole, DestinationPole);
    Hanoi(n - , AuxiliaryPole, SourcePole, DestinationPole);
}

int main(void)

{
    Hanoi(, 'A', 'B', 'C');
    system("PAUSE");
    return ;
}

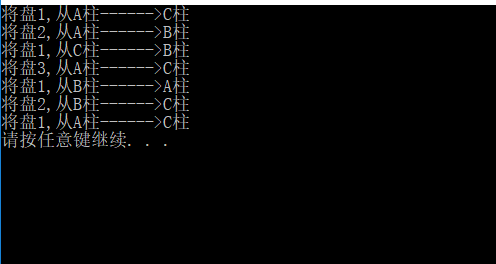
当然，对于出口也有另一种，盘数是从1~(n-1)的，当n = 0时结束入栈，当n = 1时恰好是最后一个入栈的。因此，可以当n = 1时进行一次移盘操作之后结束入栈。

此时的代码为（将SourcePole...更换变量名，便于读者阅读）：

#include <stdio.h>
#include <stdlib.h>

void Hanoi(int n, char A, char B, char C){
    if(n == ){
        return printf("将盘%d,从%c柱------>%c柱\n", n ,A, C);
    }
    Hanoi(n - , A, C, B);
    printf("将盘%d,从%c柱------>%c柱\n", n ,A, C);
    Hanoi(n - , B, A, C);
}

int main(void)
{

    Hanoi(, 'A', 'B', 'C');
    system("PAUSE");
    return ;
}

还有一道从N个球中取M个球的递归问题也不错，有兴趣可以看：点击链接

深入

接着我们对递归进行深一步的挖掘，了解递归的运算过程和在栈中的处理情况。

了解递归的运算过程，我们需知递归在栈中运算：

1. 后进先出，先进后出
2. 自顶向下移动指针

对于前面提到的n项求和，我们理解sum(6) 可以通过下面的图例理解，后进前出，先进后出的情况：

对于在栈中的运算过程我们可以结合下图理解：

递归在栈中的运算过程如下图：

图片来源

#include <bits\stdc++.h>

using namespace std;

int main()
{
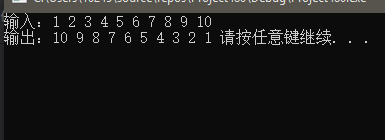
    stack<int> val;

    cout << "输入：";
    for (int i = ; i <= ; ++i) {
        cout << i << ' ';
        val.push(i);//将数据压入栈中(1~10)
    }

    cout << endl;

    cout << "输出：";
    while (!val.empty()) {
        cout << val.top() << ' ';//输出顶层数据

        val.pop();
        //删除顶层数据，下一次输出顶层数据将是原来的第二个数据
        //以此循环，直到栈中数据全部释放
    }

    system("PAUSE");
    return ;
}

二分法：

二分法顾名思义就是将数据分半进行查找。（前提是数据是按顺序排列好的）

思路（假设数组的值从小到大排列）：

1. 找到数组下标中间位置mid;
2. 将array[mid]与寻找值num比较;

若值相等结束查找，若不相等再次进行二分法查找。

具体的比较方式是：

• 若array[mid] = num 结束查找
• 若array[mid] > num 说明array{mid, mid+1... ...end} > num，则此时应该在array{beg... ...mid-1}中查找，end = mid - 1;
• 若array[mid] < num 说明array{beg, beg+1... ...mid} < num, 则此时应该在array{mid+1... ...end}中查找, beg = mid + 1；

C语言（非递归）：

#include <stdio.h>
#include <stdlib.h>

int Search(int *arr, int beg, int end, int num) {
    int mid;

    while (beg <= end) {
        mid = (beg + end) / ;//定义中间位置
        if (arr[mid] < num) {
            beg = mid + ;
            //当中间位置对应数组值小于寻找的数
            //则数组的寻找区间起点改变为 mid+1
        }
        else if (arr[mid] > num) {
            end = mid - ;
            //当中间位置对应数组值大于寻找的数
            //数组的寻找终点变为 mid - 1
        }
        else {
            return mid;
            //相等时，找到寻找的数
        }
    }

    return -;
}

int main(void)
{
    int array[] = { , , , , , ,  };

    printf("%d\n",Search(array, , , ));

    system("PAUSE");
    return ;
}

C语言（递归）

首先找出口,当beg > end时退出递归

找关系式， 三种大小关系就行，对beg和end的修改，在函数的再次调用上体现。

#include <stdio.h>
#include <stdlib.h>

int Search(int *arr, int beg, int end, int num) {
    int mid;

    while (beg <= end) {
        mid = (beg + end) / ;
        if (arr[mid] < num) {
            return (arr, mid + , end, num);
        }
        else if (arr[mid] > num) {
            return (arr, beg, mid - , num);
        }
        else {
            return mid;
        }
    }

    return -;
}

int main(void)
{
    int array[] = { , , , , , ,  };

    printf("%d\n",Search(array, , , ));

    system("PAUSE");
    return ;
}

尾递归

定义：是指一个函数里的最后一个动作是返回一个函数的调用结果的情形，即最后一步新调用的返回值直接被当前函数的返回结果。此时，该尾部调用位置被称为尾位置。尾调用中有一种重要而特殊的情形叫做尾递归。

简而言之：在执行递归操作时，将算术的结果作为参数传入。

这种方法编译器可以在下次调用函数前，销毁当前的栈空间，亦或者直接覆盖当前栈空间数据，降低了栈空间损耗，但依然存在着当前环境优化问题的问题。

有兴趣的可以看看前辈的这篇文章：点击查看

各位读者能够有收获便是我最大的快乐！写教程不易，熬夜伤身，有个赞什么的，我也是不介意滴！哈哈哈！