首先，我们要知道BFS的思想，BFS全称是Breadth-First-Search。
二叉树的BFS：通过BFS访问，它们的访问顺序是它们到根节点距离从小到大的排序。
图的BFS：同样的，离起点越近，越早被访问到。

例题1: Abbott的复仇（Abbott's Revenge，ACM/ICPC World Finals 2000，UVa 816）

题目描述：有一个最多包含9x9个交叉点的迷宫。输入起点、起始朝向、终点，求最短路。
这个迷宫的特殊之处在于：进入一个交叉点的方向不同（NEWS：N朝上，E朝右，W朝左，S朝下），允许出去的方向也不同。
例如：1 2 WLF NR ER * 表示交叉点(1,2)有三个路标，（字符*为结束标志），如果进入该交叉点时的方向为W（左），则可以L（左转）或F（直行）。如果进入时方向为N（上）或者E（右），则只能R（右转）。

如图所示：

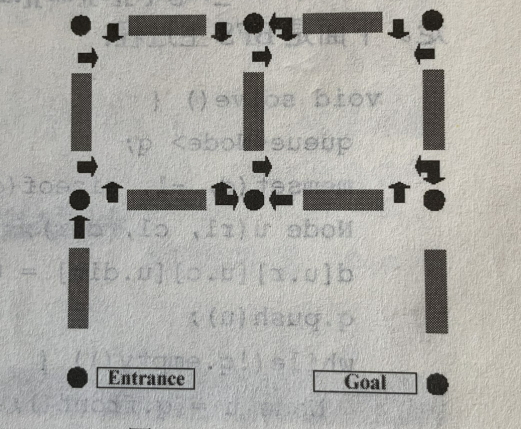
利用BFS实现最短路的更多相关文章

  1. 利用BFS求最短路

    利用BFS求图的最短路, POJ3984 #define _CRT_SECURE_NO_DEPRECATE #include<iostream> #include<string.h& ...

  2. BFS求最短路

    假设有一个n行m列的迷宫,每个单位要么是空地(用1表示)要么是障碍物(用0表示).如和找到从起点到终点的最短路径?利用BFS搜索,逐步计算出每个节点到起点的最短距离,以及最短路径每个节点的前一个节点. ...

  3. 6.4.2 用BFS求最短路

    前面的篇幅占了太多,再次新开一章,讲述BFS求最短路的问题 注意此时DFS就没有BFS好用了,因为DFS更适合求全部解,而BFS适合求最优解 这边再次提醒拓扑变换的思想在图形辨认中的重要作用,需要找寻 ...

  4. 图-用DFS求连通块- UVa 1103和用BFS求最短路-UVa816。

    这道题目甚长, 代码也是甚长, 但是思路却不是太难.然而有好多代码实现的细节, 确是十分的巧妙. 对代码阅读能力, 代码理解能力, 代码实现能力, 代码实现技巧, DFS方法都大有裨益, 敬请有兴趣者 ...

  5. POJ 2251 Dungeon Master --- 三维BFS(用BFS求最短路)

    POJ 2251 题目大意: 给出一三维空间的地牢,要求求出由字符'S'到字符'E'的最短路径,移动方向可以是上,下,左,右,前,后,六个方向,每移动一次就耗费一分钟,要求输出最快的走出时间.不同L层 ...

  6. UVa 816 (BFS求最短路)

    /*816 - Abbott's Revenge ---代码完全参考刘汝佳算法入门经典 ---strchr() 用来查找某字符在字符串中首次出现的位置,其原型为:char * strchr (cons ...

  7. CSU 1259 bfs找最短路

    题目大意: 不想介绍,题目链接:http://acm.csu.edu.cn/OnlineJudge/problem.php?id=1259 bfs求最短路. 这里因为2-9,到达同样的点不计步数,那我 ...

  8. UVA 816 -- Abbott's Revenge(BFS求最短路)

     UVA 816 -- Abbott's Revenge(BFS求最短路) 有一个 9 * 9 的交叉点的迷宫. 输入起点, 离开起点时的朝向和终点, 求最短路(多解时任意一个输出即可).进入一个交叉 ...

  9. [蓝桥杯2015决赛]穿越雷区（BFS求最短路）

    题目描述 X星的坦克战车很奇怪,它必须交替地穿越正能量辐射区和负能量辐射区才能保持正常运转,否则将报废.某坦克需要从A区到B区去(A,B区本身是安全区,没有正能量或负能量特征),怎样走才能路径最短?已 ...

随机推荐

  1. Redis雪崩、穿透、热点key等优化

    一.缓存 Redis做缓存是最常见的应用场景.客户端请求在缓存层命中就直接返回,如果miss就去读取存储层,存储层读取到就写入缓存层,然后再返回到客户端. 优点: 加速读写 降低后端负载 缺点: 数据 ...

  2. Coursera-AndrewNg(吴恩达)机器学习笔记——第三周编程作业（逻辑回归）

    一. 逻辑回归 1.背景:使用逻辑回归预测学生是否会被大学录取. 2.首先对数据进行可视化,代码如下: pos = find(y==); %找到通过学生的序号向量 neg = find(y==); % ...

  3. C++设计模式 ==> 装饰（者）模式

    简介 装饰模式指的是在不必改变原类文件和使用继承的情况下,动态地扩展一个对象的功能.它是通过创建一个包装对象,也就是装饰来包裹真实的对象.装饰模式使用对象嵌套的思想,实现对一个对象动态地进行选择性的属 ...

  4. 牢记 31 种 CSS 选择器用法

    原文 The 30 CSS Selectors you Must Memorize 由 Jeffrey Way 发表于 2011 年 6 月,介绍了 30 种最常用的 CSS 选择器用法,多加了一种, ...

  5. 复杂json的解析：jsonobject与jsonArray的使用

    String parameter = { success : 0, errorMsg : "错误消息", data : { total : "总记录数", ro ...

  6. 5.Dubbo2.5.3泛化引用和泛化实现

    转载请出自出处:http://www.cnblogs.com/hd3013779515/ 1.泛化引用 泛接口调用方式主要用于客户端没有API接口及模型类元的情况,参数及返回值中的所有POJO均用Ma ...

  7. react如何引入外部文件的整理

    1 引入组件 首先就应该是安装了,安装在环境中后通过 import { Select, Button, Icon, QueueAnim } from 'antd'; 就可以把需要的组件引用进来了~ 2 ...

  8. HTML标签之marquee

    版权声明:本文为博主原创文章.未经博主同意不得转载. https://blog.csdn.net/zkn_CS_DN_2013/article/details/25229719 <html> ...

  9. RMAN常用命令汇总！

    进入RMAN:$ rman target sys/oracle@orcl   --远程连接到rman$ rman target sys/oracle@orcl @backup_db.ram   --远 ...

  10. python-webbrowser模块 浏览器操作

    python的webbrowser模块支持对浏览器进行一些操作,对于爬虫来说是比较基础的知识点 1.主要有以下三个方法: webbrowser.open(url, new=0, autoraise=T ...