JavaScript动画实例:圆点的衍生
考虑如下的曲线方程:
R=S*sqrt(n)
α=n*θ
X=R*SIN(α)
Y=R*COS(α)
其中,S和θ可指定某一个定值。对n循环取0~999共1000个值,对于每个n,按照给定的坐标方程,求得一个坐标值(x,y),然后以(x,y)为圆心绘制一个半径为6的圆,可以得到一个螺旋状的图形。
编写如下的HTML代码。
<html>
<head>
<title>衍生的圆点</title>
</head>
<body>
<canvas id="myCanvas" width="600" height="600" style="border:3px double #996633;">
</canvas>
<script>
var canvas = document.getElementById('myCanvas');
var ctx = canvas.getContext('2d');
var scale = 10;
var theta = 30;
for (n=0;n<1000;n++)
{
var radius = scale * Math.sqrt(n);
var angle = n * theta * (Math.PI / 180);
var x = radius * Math.cos(angle) + canvas.width / 2;
var y = radius * Math.sin(angle) + canvas.height / 2;
ctx.beginPath();
ctx.arc(x, y, 6, 0, Math.PI * 2);
ctx.fillStyle ='rgba(255,50,50,0.9)';
ctx.fill();
}
</script>
</body>
</html>
在浏览器中打开包含这段HTML代码的html文件,可以看到在画布中绘制出如图1所示的图案。
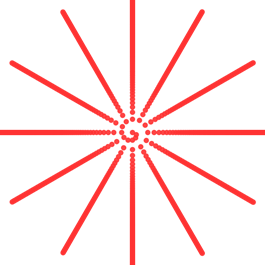
图1 scale = 10,theta = 30时绘制的图案
若将上面程序中的语句“var theta = 30; ”改写为“var theta =60; ”,其余部分保持不变,则在画布中绘制出如图2所示的图案。

图2 scale = 10,theta = 60时绘制的图案
在程序中,theta代表每个小圆圆心相对于上一个小圆圆心的偏移角度。一个圆周360°,因此当theta = 30时,会绘制出360/30=12条放射状的线,如图1所示;当theta =60时,会绘制出360/60=6条放射状的线,如图2所示。
若将上面程序中的语句“var theta = 30; ”改写为“var theta =110; ”,其余部分保持不变,则在画布中绘制出如图3所示的图案。

图3 scale = 10,theta =110时绘制的图案
若再将程序中的语句“var scale = 10; ”改写为“var scale =6; ”,则在画布中绘制出如图4所示的图案。

图4 scale = 6,theta =110时绘制的图案
若将程序中的语句“var scale = 10; ”改写为“var scale =15; ”,则在画布中绘制出如图5所示的图案。

图5 scale = 15,theta =110时绘制的图案
对比图3、4、5可知,scale的值可以可知各小圆的疏密程度。
将上面程序中1000个小圆的绘制过程动态展示出来,编写如下的HTML文件。
<html>
<head>
<title>衍生的圆点</title>
</head>
<body>
<canvas id="myCanvas" width="600" height="600" style="border:3px double #996633;background:black;">
</canvas>
<script>
var canvas = document.getElementById('myCanvas');
var ctx = canvas.getContext('2d');
var hue = 0;
var scale = 10;
var n = 0;
var theta = 30;
function draw()
{
var radius = scale * Math.sqrt(n);
var angle = n * theta * (Math.PI / 180);
var x = radius * Math.cos(angle) + canvas.width / 2;
var y = radius * Math.sin(angle) + canvas.height / 2;
hue++;
if (hue >= 360) hue = 0;
ctx.beginPath();
ctx.arc(x, y, 6, 0, Math.PI * 2);
ctx.fillStyle = `hsl(${hue}, 100%, 50%)`;
ctx.fill();
n++;
if (n>=1000)
{
ctx.clearRect(0,0,canvas.width,canvas.height);
n=0;
}
}
setInterval("draw()",20);
</script>
</body>
</html>
在浏览器中打开包含这段HTML代码的html文件,可以看到在浏览器窗口中呈现出如图6所示的动画效果。

图6 scale = 10,theta = 30时圆点衍生效果
更改scale和theta的值,会产生不同的圆点衍生效果。例如,修改scale=12,theta=137.5,则在浏览器窗口中呈现出如图7所示的动画效果。

图7 scale = 12,theta = 137.5时圆点衍生效果
更进一步,我们将上面程序中的控制圆点疏密程度的参数scale和每次迭代偏移角度theta采用随机数的方式确定其值。编写如下的HTML代码。
<html>
<head>
<title>衍生的圆点</title>
</head>
<body>
<canvas id="myCanvas" width="400" height="400" style="border:3px double #996633;background:black;"></canvas>
<script>
var canvas = document.getElementById('myCanvas');
var ctx = canvas.getContext('2d');
var hue = 0;
var scale = 12;
var n = 0;
var theta = 137.5;
function rand(min,max)
{
return Math.floor(Math.random()*(max-min)+min)+(Math.random()>0.5?0.5:0);
}
function draw()
{
var radius = scale * Math.sqrt(n);
var angle = n * theta * (Math.PI / 180);
var x = radius * Math.cos(angle) + canvas.width / 2;
var y = radius * Math.sin(angle) + canvas.height / 2;
hue++;
if (hue >= 360) hue = 0;
ctx.beginPath();
ctx.arc(x, y, 6, 0, Math.PI * 2);
ctx.fillStyle = `hsl(${hue}, 100%, 50%)`;
ctx.fill();
n++;
if (n>=500)
{
ctx.clearRect(0,0,canvas.width,canvas.height);
scale=rand(6,15);
theta=rand(20,170);
n=0;
}
}
setInterval("draw()",20);
</script>
</body>
</html>
在浏览器中打开包含这段HTML代码的html文件,可以看到在浏览器窗口中呈现出如图8所示的动画效果。

图8 圆点的衍生动画特效
JavaScript动画实例:圆点的衍生的更多相关文章
- JavaScript动画实例:李萨如曲线
在“JavaScript图形实例:阿基米德螺线”和“JavaScript图形实例:曲线方程”中,我们学习了利用曲线的方程绘制曲线的方法.如果想看看曲线是怎样绘制出来的,怎么办呢?编写简单的动画,就可以 ...
- JavaScript动画实例:递归分形图动态展示
在“JavaScript图形实例:SierPinski三角形” 和“JavaScript图形实例:Levy曲线及其变形”等文章中我们介绍了通过递归生成分形图形的方法.我们可以将绘制的分形图形每隔一定的 ...
- JavaScript动画实例:曲线的绘制
在“JavaScript图形实例:曲线方程”一文中,我们给出了15个曲线方程绘制图形的实例.这些曲线都是根据其曲线方程,在[0,2π]区间取一系列角度值,根据给定角度值计算对应的各点坐标,然后在计算出 ...
- JavaScript动画实例:旋转的圆球
1.绕椭圆轨道旋转的圆球 在Canvas画布中绘制一个椭圆,然后在椭圆上绘制一个用绿色填充的实心圆.之后每隔0.1秒刷新,重新绘制椭圆和实心圆,重新绘制时,实心圆的圆心坐标发生变化,但圆心坐标仍然位于 ...
- JavaScript动画实例:动感小球
已知圆的坐标方程为: X=R*SIN(θ) Y=R*COS(θ) (0≤θ≤2π) 将0~2π区间等分48段,即设定间隔dig的值为π/24.θ初始值从0开始,按曲线方程求得坐标值(x,y), ...
- JavaScript动画实例:旋转的正三角形
给定一个正三角形的重心坐标为(x0,y0),高为h,可以用如下的语句绘制一个底边水平的正三角形. ctx.beginPath(); ctx.moveTo(x0,y0-h*2/3); ctx.lineT ...
- JavaScript动画实例:沿五角星形线摆动的小圆
五角星形线的笛卡尔坐标方程式可设为: r=10+(3*sin(θ*2.5))^2 x=r*cos(θ) y=r*sin(θ) (0≤θ≤2π) 根据这个曲线方程,在[0,2 ...
- JavaScript动画实例:炸开的小球
1.炸开的小球 定义一个小球对象类Ball,它有6个属性:圆心坐标(x,y).小球半径radius.填充颜色color.圆心坐标水平方向的变化量speedX.圆心坐标垂直方向的变化量speedY. B ...
- JavaScript动画实例:螺旋线
数学中有各式各样富含诗意的曲线,螺旋线就是其中比较特别的一类.螺旋线这个名词来源于希腊文,它的原意是“旋卷”或“缠卷”.例如,平面螺旋便是以一个固定点开始向外逐圈旋绕而形成的曲线.在2000多年以前, ...
随机推荐
- 上海python14期第一次周考
上海python14期第一次周考 1 介绍 满分50分 考试范围: Python语法 数据类型 流程控制 考试时间: 周五下午3.00点-晚6:00 2 基础题(38分) 什么是编程语言?什么是语言? ...
- Jmeter系列(41)- Jmeter + Ant +Jenkins 持续集成
如果你想从头学习Jmeter,可以看看这个系列的文章哦 https://www.cnblogs.com/poloyy/category/1746599.html Window 环境准备 安装 ant: ...
- Python并发编程——多线程与协程
Pythpn并发编程--多线程与协程 目录 Pythpn并发编程--多线程与协程 1. 进程与线程 1.1 概念上 1.2 多进程与多线程--同时执行多个任务 2. 并发和并行 3. Python多线 ...
- mui div滚动阻止触发下拉刷新
function orderListScroll () { var _orderObj = document.querySelector('.circulation-loan-list') //div ...
- java 面向对象(二十五):内部类:类的第五个成员
内部类:类的第五个成员 1.定义: Java中允许将一个类A声明在另一个类B中,则类A就是内部类,类B称为外部类.2.内部类的分类:成员内部类(静态.非静态 ) vs 局部内部类(方法内.代码块内.构 ...
- java 面向对象(十六):Object类的使用
1.java.lang.Object类的说明: * 1.Object类是所Java类的根父类 * 2.如果在类的声明中未使用extends关键字指明其父类,则默认父类为java.lang.Object ...
- SQLAlchemy03 /外键、连表关系
SQLAlchemy03 /外键.连表关系 目录 SQLAlchemy03 /外键.连表关系 1.外键 2.ORM关系以及一对多 3.一对一的关系 4.多对多的关系 5.ORM层面的删除数据 6.OR ...
- Python之爬虫从入门到放弃(十三) Scrapy框架整体的了解
这里是通过爬取伯乐在线的全部文章为例子,让自己先对scrapy进行一个整理的理解 该例子中的详细代码会放到我的github地址:https://github.com/pythonsite/spider ...
- layui弹窗里面 session过期 后跳转到登录页面
1.在登录页面添加 <script> $(function () { if (top != window) { layer.msg("登录失效", {icon: 5}) ...
- ffmpeg播放器实现详解 - 框架搭建
ffplay是ffmpeg源码中一个自带的开源播放器实例,同时支持本地视频文件的播放以及在线流媒体播放,功能非常强大. FFplay: FFplay is a very simple and port ...
