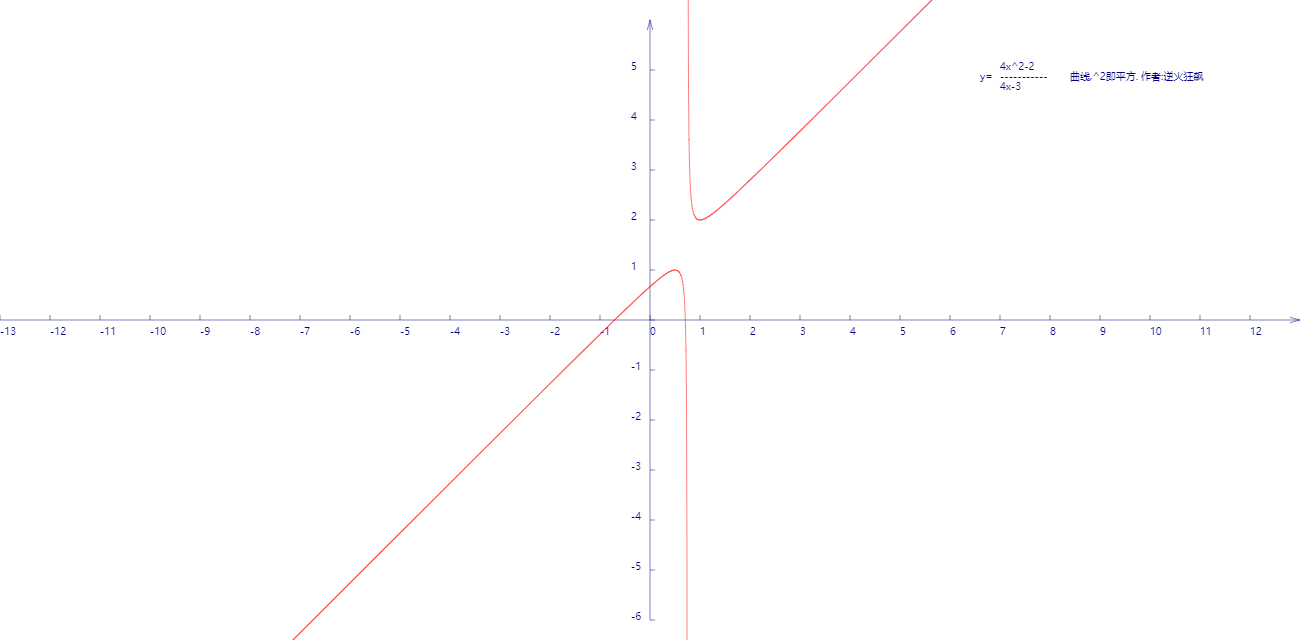
代码：

<!DOCTYPE html>
<html lang="utf-8">
<meta http-equiv="Content-Type" content="text/html; charset=utf-8"/>
<head>
     <title>函数4x^2-2/4x-3曲线勾画</title>
    </head>

     <body onload="draw()">
        <canvas id="myCanvus" width="1300px" height="640px" style="border:1px dashed black;">
            出现文字表示你的浏览器不支持HTML5
        </canvas>
     </body>
</html>
<script type="text/javascript">
<!--
    function draw(){
        var canvas=document.getElementById("myCanvus");
        var canvasWidth=1300;
        var canvasHeight=640;

        var context=canvas.getContext("2d");

        context.fillStyle = "white";
        context.fillRect(0, 0, canvasWidth, canvasHeight);

        context.strokeStyle = "black";
        context.fillStyle = "black";

        // 进行坐标变换：把原点放在左下角，东方为X轴正向，北方为Y轴正向
        var offsetY=320;// Y向偏移值，正值向上偏，用来画坐标轴
        var offsetX=650;// X向偏移值，正值向右偏，用来画坐标轴

        context.save();
        context.translate(0+offsetX,canvasHeight-offsetY);

        drawAxisXText(context);// 文字和线分开画比较好处理
        drawAxisYText(context);
        drawTitleText(context);

        context.rotate(getRad(180));
        context.scale(-1,1);        

        drawAxisX(context);
        drawAxisY(context);
        drawCurve(context);       

        context.restore();
    }

    function drawTitleText(ctx){
        ctx.lineWidth=0.5;
        ctx.strokeStyle='navy';
        ctx.fillStyle='navy';

        var x=350;
        var y=-250;

        // 写文字
        ctx.fillText("4x^2-2",x,y);
        ctx.fillText("-----------",x,y+10);
        ctx.fillText("4x-3",x,y+20);
        ctx.fillText("y=",x-20,y+10);
        ctx.fillText("曲线,^2即平方. 作者:逆火狂飙",x+70,y+10);
    }

    function drawCurve(ctx){
        var SU=50;// Scale Unit

        var cds=[{}];
        var cds2=[{}];

        var x,y;
        for(x=-13;x<=13;x+=0.01){

            if(x<3/4){
                y=(4*x*x-2)/(4*x-3);// 函数式在此
                var arr={"x":x,"y":y};
                cds.push(arr);
            }

            if(x>3/4){
                y=(4*x*x-2)/(4*x-3);// 函数式在此
                var arr={"x":x,"y":y};
                cds2.push(arr);
            }
        }

        // 将数组里面的点一段段连线
        //var ymax=-6,ymin=6,xmax,xmin;

        ctx.strokeStyle = "red";
        ctx.beginPath();

        for(var i=0; i<cds.length; i++){
            ctx.lineTo(cds[i].x*SU,cds[i].y*SU);
        } 

        ctx.stroke();
        ctx.closePath();

        ctx.beginPath();
        for(var i=0; i<cds2.length; i++){
            ctx.lineTo(cds2[i].x*SU,cds2[i].y*SU);
        } 

        ctx.stroke();
        ctx.closePath();

        // 极大值
        /*ctx.beginPath();
        ctx.moveTo(xmax*SU,ymax*SU-5);
        ctx.lineTo(xmax*SU,ymax*SU+5);

        ctx.save();
        ctx.scale(1,-1);
        ctx.fillText("ymax="+cutShort(ymax.toString(),8),xmax*SU,-ymax*SU);
        ctx.restore();

        ctx.stroke();
        ctx.closePath();

        // 极小值
        ctx.beginPath();
        ctx.moveTo(xmin*SU,ymin*SU-5);
        ctx.lineTo(xmin*SU,ymin*SU+5);

        ctx.save();
        ctx.scale(1,-1);
        ctx.fillText("ymin="+ymin,xmin*SU,-ymin*SU);
        ctx.restore();

        ctx.stroke();
        ctx.closePath();*/
    }

    function drawAxisX(ctx){
        ctx.save();

        ctx.lineWidth=0.5;
        ctx.strokeStyle='navy';
        ctx.fillStyle='navy';

        var start=-650;
        var end=650;

        // 画轴
        ctx.beginPath();
        ctx.moveTo(start, 0);
        ctx.lineTo(end, 0);
        ctx.stroke();
        ctx.closePath();

        // 画箭头
        ctx.beginPath();
        ctx.moveTo(end-Math.cos(getRad(15))*10, Math.sin(getRad(15))*10);
        ctx.lineTo(end, 0);
        ctx.lineTo(end-Math.cos(getRad(15))*10, -Math.sin(getRad(15))*10);
        ctx.stroke();
        ctx.closePath();

        // 画刻度
        var x,y;
        y=5;
        for(x=start;x<end;x+=50){
            ctx.beginPath();
            ctx.moveTo(x, 0);
            ctx.lineTo(x, y);

            ctx.stroke();
            ctx.closePath();
        }

        ctx.restore();
    }

    function drawAxisXText(ctx){
        ctx.lineWidth=0.5;
        ctx.strokeStyle='navy';
        ctx.fillStyle='navy';

        var start=-650;
        var end=650;

        // 写文字
        var x,y=5;
        for(x=start;x<end;x+=50){
            ctx.fillText(x/50,x,y+10);
        }
    }

    function drawAxisY(ctx){
        ctx.save();

        ctx.lineWidth=0.5;
        ctx.strokeStyle='navy';
        ctx.fillStyle='navy';

        var start=-300;
        var end=300;

        // 画轴
        ctx.beginPath();
        ctx.moveTo(0, start);
        ctx.lineTo(0, end);
        ctx.stroke();
        ctx.closePath();

        // 画箭头
        ctx.beginPath();
        ctx.moveTo(Math.sin(getRad(15))*10, end-Math.cos(getRad(15))*10);
        ctx.lineTo(0, end);
        ctx.lineTo(-Math.sin(getRad(15))*10, end-Math.cos(getRad(15))*10);
        ctx.stroke();
        ctx.closePath();

        // 画刻度
        var x,y;
        x=5;
        for(y=start;y<end;y+=50){
            ctx.beginPath();
            ctx.moveTo(x, y);
            ctx.lineTo(0, y);

            ctx.stroke();
            ctx.closePath();
        }
    }

    function drawAxisYText(ctx){
        ctx.lineWidth=0.5;
        ctx.strokeStyle='navy';
        ctx.fillStyle='navy';

        var start=-250;
        var end=350;

        // 写文字
        var x=-19,y=5;
        for(y=start;y<end;y+=50){

            if(y!=0){
                ctx.fillText(-y/50,x,y);
            }
        }
    }

    function getRad(degree){
        return degree/180*Math.PI;
    }

    function cutShort(str,length){
        if(str.length>length){
            str=str.substr(0,length)+"...";
        }

        return str;
    }
//-->
</script>

在笛卡尔坐标系上描绘函数 y=4x^2-2/4x-3的更多相关文章

  1. 在笛卡尔坐标系上描绘函数(x*x+1)/(x*x-1)曲线

    代码: <!DOCTYPE html> <html lang="utf-8"> <meta http-equiv="Content-Type ...

  2. 在笛卡尔坐标系上描绘函数2*x+Math.sqrt(5-x*x)及其共轭函数2*x-Math.sqrt(5-x*x)曲线

    代码如下: <!DOCTYPE html> <html lang="utf-8"> <meta http-equiv="Content-Ty ...

  3. 在笛卡尔坐标系上描绘y=x^2-4/x^2-2x-3曲线

    <!DOCTYPE html> <html lang="utf-8"> <meta http-equiv="Content-Type&quo ...

  4. AcWing：112. 雷达设备（贪心 + 笛卡尔坐标系化区间）

    假设海岸是一条无限长的直线,陆地位于海岸的一侧,海洋位于另外一侧. 每个小岛都位于海洋一侧的某个点上. 雷达装置均位于海岸线上,且雷达的监测范围为d,当小岛与某雷达的距离不超过d时,该小岛可以被雷达覆 ...

  5. HTML5 Canvas 笛卡尔坐标系转换尝试

    <!DOCTYPE html> <html lang="utf-8"> <meta http-equiv="Content-Type&quo ...

  6. 如果是在有master上开启了该参数，记得在slave端也要开启这个参数（salve需要stop后再重新start），否则在master上创建函数会导致replaction中断。

    如果是在有master上开启了该参数,记得在slave端也要开启这个参数(salve需要stop后再重新start),否则在master上创建函数会导致replaction中断.

  7. 使用神经网络来拟合函数y = x^3 +b

    我们使用一个三层的小网络来,模拟函数y = x^3+b函数 import tensorflow as tf import numpy as np import matplotlib.pyplot as ...

  8. 自学Linux Shell16.4-在命令行上使用函数

    点击返回 自学Linux命令行与Shell脚本之路 16.4-在命令行上使用函数 脚本函数不仅可以用作shell脚本命令,也可以用作命令行界面的命令.一旦在shell中定义了函数,可以从系统的任意目录 ...

  9. 函数 y=x^x的分析

    关于函数 y=xx的分析: 由图像得,y在负无穷大到0图像处处不连续,故y的定义域为(0,正无穷大): 故该函数不就是y=e^(lnxx)吗? 1.定义域:我们变形一下,y=e^(xlnx),显然是0 ...

随机推荐

  1. H264 帧边界识别简介

    http://blog.csdn.net/wzw88486969/article/details/50364017

  2. CentOS 7 Docker

    安装docker yum install docker 查看docker docker version 这是因为docker还没有运行,需要启动docker 启动docker systemctl st ...

  3. HDU6074 Phone Call （并查集 LCA）

    Phone Call Time Limit: 6000/3000 MS (Java/Others)    Memory Limit: 524288/524288 K (Java/Others)Tota ...

  4. Sqli-labs介绍、下载、安装

    SQLI和sqli-labs介绍 SQLI,sql injection,我们称之为sql注入.何为sql,英文:Structured Query Language,叫做结构化查询语言.常见的结构化数据 ...

  5. Html导出Pdf

    最近领导给了一个新的需求:给了我一个html页面,让我导出Pdf页面 由于以前没有搞过这方面的需求,所以查百度找资料,找了一大堆的好东西,像ItextSharp和wkhtmltopdf 废话不说,进入 ...

  6. 有的系统区apk需要对其系统签名，才能正常使用。

    韩梦飞沙  韩亚飞  313134555@qq.com  yue31313  han_meng_fei_sha 向方案公司索要platform.x509.pem 和platform.pk8这两个文件. ...

  7. 手机上编程，编写android apk

    韩梦飞沙 yue31313 韩亚飞 han_meng_fei_sha  313134555@qq.com C4Droid:在手机上直接编程,然后导出为apk

  8. JZYZOJ1536 [haoi2014]走出金字塔

    http://172.20.6.3/Problem_Show.asp?id=1536 确实不难,找规律的题,开始想复杂了,分了好多情况.开始为省几个变量加了一大堆max,min,abs代码一下子复杂太 ...

  9. 【树形dp】The more, The Better

    [HDU1561]The more, The Better Time Limit: 6000/2000 MS (Java/Others)    Memory Limit: 32768/32768 K ...

  10. 【二分】Petrozavodsk Winter Training Camp 2017 Day 1: Jagiellonian U Contest, Monday, January 30, 2017 Problem A. The Catcher in the Rye

    一个区域,垂直分成三块,每块有一个速度限制,问你从左下角跑到右上角的最短时间. 将区域看作三块折射率不同的介质,可以证明,按照光路跑时间最短. 于是可以二分第一个入射角,此时可以推出射到最右侧边界上的 ...