Wannafly 挑战赛16 A 取石子

题目描述

给出四堆石子，石子数分别为a,b,c,d。规定每次只能从堆顶取走石子，问取走所有石子的方案数。

输入描述:

在一行内读入四个由空格分隔的整数a,b,c,d， 输入均为不超过500的正整数

输出描述:

输出一个整数表示答案，答案对10⁹+7取模

示例1

输入

3 5 4 2

输出

2522520

备注:

输入均为不超过500的正整数

【分析】

每一堆的石子之间的相对位置是固定不变的，所以可以通过插入来生成一个取石子的顺序，而插入的求解则可以利用组合数来计算。 起始的时候，把第一堆的$$$a$$$个石头摆好，相当于在$$$a$$$个空位放下$$$a$$$个石头，由于石头顺序是固定的，所以有$$$C^a_a$$$种，也就是1种；

接下来，把第二堆的$$$b$$$个石头也加进来，要在$$$a$$$个石头之间以及两边插入$$$b$$$个石头，等价于一共有$$$a+b$$$个位置，在其中选$$$b$$$个位置，作为放置$$$b$$$的地方，由于$$$b$$$的顺序确定，所以组合数为$$$C^b_{a+b}$$$个

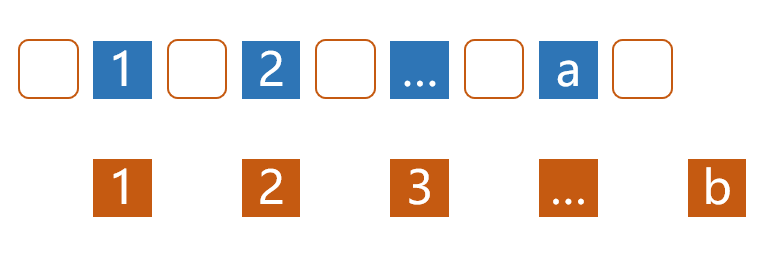
然后把第三堆的$$$c$$$个石头也加进来，在$$$a+b$$$个石头插入$$$c$$$个石头，同理，组合数为$$$C^c_{a+b+c}$$$个；

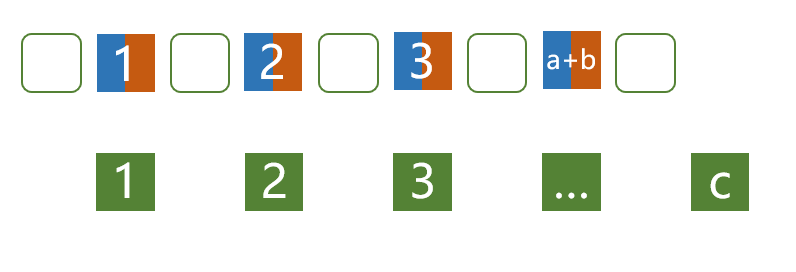
第四堆的$$$d$$$加进来就是$$$C^d_{a+b+c+d}$$$个。 所以最终答案为$$$C^a_a \times C^b_{a+b} \times C^c_{a+b+c} \times C^d_{a+b+c+d}$$$个

【注意】

组合数较大需要用long long存放；对答案需要取模 可以对组合数打表，来避免分数取模，公式为$$$C^x_y = C^x_{y-1} + C^{x-1}_{y-1}$$$

【代码】

#include<stdio.h>
#define N_max 2005
int n;
typedef long long ll;
#define mod 1000000007

ll C[N_max][N_max] = { 0 };
#define min(a,b) ((a)<(b)?(a):(b))

int main() {

int a[4];
	ll res = 1;
	for (int t = 0; t < N_max; ++t)C[t][0]=1;

	for (int i = 1; i <N_max; ++i)
		for (int j = 1; j <=i; ++j) {
			C[i][j] = (C[i - 1][j - 1] + C[i - 1][j])%mod;
		}
	for (int i = 0; i < 4; ++i)
	{
		scanf("%d", a + i);
	}
	res = C[a[0]][a[0]];
	res = res*C[a[0] + a[1]][a[1]]%mod;
	res = res*C[a[0] + a[1]+a[2]][a[2]]%mod;
	res = res*C[a[0] + a[1]+a[2]+a[3]][a[3]]%mod;

	printf("%lld", res);
	return 0;
}