poj2018——Best Cow Fences

Description

Farmer John's farm consists of a long row of N (1 <= N <= 100,000)fields. Each field contains a certain number of cows, 1 <= ncows <= 2000.

FJ wants to build a fence around a contiguous group of these fields
in order to maximize the average number of cows per field within that
block. The block must contain at least F (1 <= F <= N) fields,
where F given as input.

Calculate the fence placement that maximizes the average, given the constraint.

Input

* Line 1: Two space-separated integers, N and F.

* Lines 2..N+1: Each line contains a single integer, the number of
cows in a field. Line 2 gives the number of cows in field 1,line 3 gives
the number in field 2, and so on.

Output

* Line
1: A single integer that is 1000 times the maximal average.Do not
perform rounding, just print the integer that is 1000*ncows/nfields.

Sample Input

10 6
6
4
2
10
3
8
5
9
4
1

Sample Output

6500

题意：

给定一个正整数序列a，求一个平均数最大的、长度不小于L的子段。

Solution：

本题由于是求平均数的最大值，我们很容易往二分方向上想，二分答案的关键是如何取check，判定“是否存在一个长度不小与L的子段平均数不小于二分的值”。

考虑这样一种思路，把数列中每个数都减去二分的值，就转化为判断是否存在一个长不小于L的子段，子段和非负。继续思考，

1、若没有L的限制，只需O(n)扫描数列不断加数当和为负数时就把当前子段清空，扫描过程中出现过的最大子段和即为所求。

2、求一个子段它的和最大且长度不小与L。子段和可以转化为前缀和相减的形式，即设sum_i表示a_i～a_j的和，则：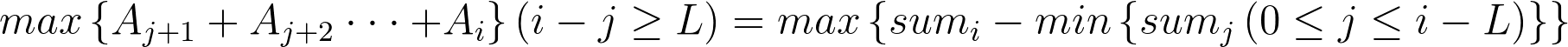

仔细观察上面的式子容易发现，随着i的增长，j的取值范围0～i-L每次只会增大1。换言之，每次只会有一个新的取值进入min{sum_j}的候选集合，所以我们没有必要每次循环枚举j，只需要用一个变量记录当前的最小值，每次与新的取值sum_i-L取min就可以了。

于是我们只需要看一下最大子段和是不是非负数就可以确定二分上下界的变化范围了。

（没看懂没事，第一遍我也没看懂，仔细看并对照代码，f**k真的简单巧妙！）

代码：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<cstdlib>
#define il inline
#define ll long long
#define debug printf("%d %s\n",__LINE__,__FUNCTION__)
using namespace std;
il int gi()
{
    int a=;char x=getchar();bool f=;
    while((x<''||x>'')&&x!='-')x=getchar();
    if(x=='-')x=getchar(),f=;
    while(x>=''&&x<='')a=a*+x-,x=getchar();
    return f?-a:a;
}
const double eps=1e-;
int n,L;
double a[],b[],sum[];
int main()
{
    n=gi(),L=gi();
    for(int i=;i<=n;i++)a[i]=gi();
    double l=-1e6,r=1e6;
    while(r-l>eps){
        double mid=(l+r)/,ans=-1e10,minn=1e10;
        for(int i=;i<=n;i++)b[i]=a[i]-mid;
        for(int i=;i<=n;i++)sum[i]=sum[i-]+b[i];
        for(int i=L;i<=n;i++)minn=minn<sum[i-L]?minn:sum[i-L],ans=max(ans,sum[i]-minn);
        if(ans>=)l=mid;else r=mid;
    }
    printf("%d\n",int(r*));
    return ;
}