P3574 [POI2014] FAR-FarmCraft 吐槽 + 题解

洛谷上面的题解写的真的不太好，有很多错误，我来谈谈自己的理解。

设 \(f[i]\) 表示以 \(i\) 为根节点的子树中（包括节点 \(i\)）的所有人安装好游戏所需要的时间（与下面的 \(g[i]\) 并没有包含关系，管理员也没有强制性要求要回到根节点，比如会出现下图情况）。

设 \(g[i]\) 表示从 \(i\) 开始往下走，兜一圈又回到 \(i\) 所需要的时间。

实际上 \(f[i]\) 可能 \(< g[i]\)，比如当出现如下情况的时候：

假设下图中所有人的安装时间为 \(1\)，

那么当管理员兜了一个圈，第二次到达 \(3\) 的时候，

所有人都已经安装完成了。

所以在此图中 \(f[1] < g[1]\)。

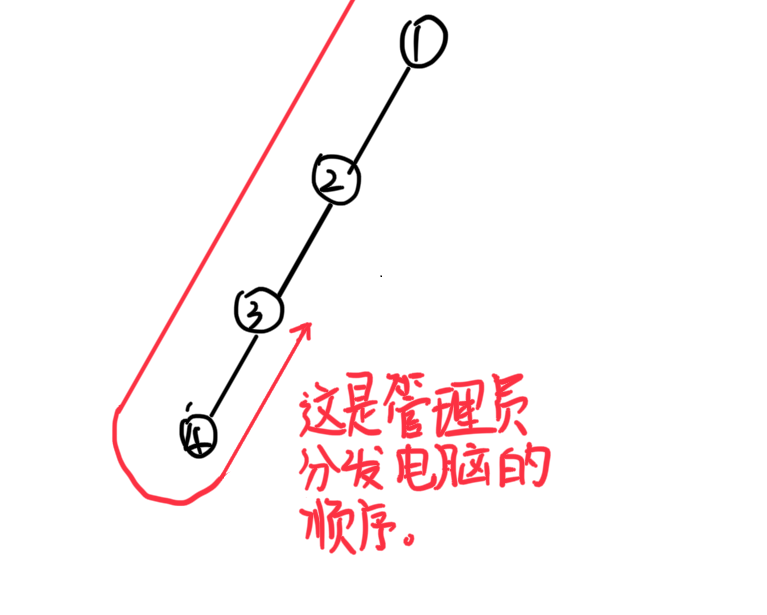
那我们先访问那个节点呢？

分为两种情况考虑，即 \(f[i] - g[i] \geq 0\) 和 \(f[i] - g[i] < 0\) 两种情况。

如果管理员回到了起点那些人还没有装完（即 \(f[i] - g[i] \geq 0\)），那么就需要等待 \(f[i] - g[i]\) 的时间所有人才能安装好。

根据常识，在等待的这段时间我们可以去下一家，以减少所需的总时间。

这里我们利用贪心，让需要等待时间最久的作为第一个访问的节点，

这样可以管理员在他漫长的安装时间内将电脑送给其他人。

而如果出现了像上图一样的情况（即 \(f[i] - g[i] < 0\)） 的情况，

根本就不需要等待，

也就不用排序，

随机访问即可，

但为了简单起见，

排了序也没有什么问题。

所以我们可以对 \(f[i] - g[i]\) 从大到小进行排序。

再挨个访问即可。

然后就是利用 \(f\) 和 \(g\) 来用子树信息更新父亲节点。

如下图：

先说结论：只安装到 \(i\) 点会需要 \(\sum (g[j] + 2) + 1 + f[i]\) 的时间能完成安装，其中 \(j\) 为比 \(i\) 先遍历到的同一层的节点（如上图）。

为什么是这样呢？

第一部分的 \(\sum (g[j] + 2)\) 表示遍历完所有 \(j\) 子树的节点，每次都回到根节点（所以要 \(+2\)）。

第二部分的 \(+1\) 表示从根节点走到 \(i\) 所需要的步骤（即为 \(1\) 步）。

最后一部分的 \(f[i]\) 表示把 \(i\) 子树内所有的游戏装好了需要花的时间。

总时间取 \(\max\) 即可， 即 \(f[root] = \max\{\sum (g[j] + 2) + f[i] + 1\}\)。

#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>

using namespace std;

const int N = 500010;

struct Edge {
	int to, next;
}e[N * 2];

int head[N], idx;

void add(int a, int b) {
	idx++;
	e[idx].to = b;
	e[idx].next = head[a];
	head[a] = idx;
}

int n, t[N];
int f[N], g[N];

void dfs(int u, int fa) {
	vector<int> wait;
	for (int i = head[u]; i; i = e[i].next) {
		int to = e[i].to;
		if (to == fa) continue;
		dfs(to, u);
		wait.push_back(to);
	}
	sort(wait.begin(), wait.end(), [](const int& a, const int& b) { return f[a] - g[a] > f[b] - g[b]; });
	for (int i = 0; i < wait.size(); i++) {
		f[u] = max(f[u], g[u] + 1 + f[wait[i]]);
		g[u] += g[wait[i]] + 2;
	}
	if (t[u] > g[u] && u != 1) f[u] = max(f[u], t[u]);
}

int main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);

	cin >> n;
	for (int i = 1; i <= n; i++) cin >> t[i];
	for (int i = 1; i < n; i++) {
		int a, b;
		cin >> a >> b;
		add(a, b);
		add(b, a);
	}
	dfs(1, 0);
	cout << max(f[1], g[1] + t[1]) << '\n';
	return 0;
}