神经网络优化篇：详解梯度的数值逼近（Numerical approximation of gradients）

在实施backprop时，有一个测试叫做梯度检验，它的作用是确保backprop正确实施。因为有时候，虽然写下了这些方程式，却不能100%确定，执行backprop的所有细节都是正确的。为了逐渐实现梯度检验，首先说说如何计算梯度的数值逼近。

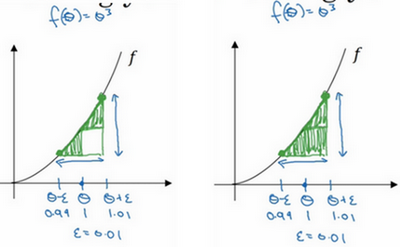
先画出函数\(f\)，标记为\(f\left( \theta \right)\)，\(f\left( \theta \right)=\theta^{3}\)，先看一下\(\theta\)的值，假设\(\theta=1\)，不增大\(\theta\)的值，而是在\(\theta\) 右侧，设置一个\(\theta +\varepsilon\)，在\(\theta\)左侧，设置\(\theta -\varepsilon\)。因此\(\theta=1\)，\(\theta +\varepsilon =1.01,\theta -\varepsilon =0.99\),，跟以前一样，\(\varepsilon\)的值为0.01，看下这个小三角形，计算高和宽的比值，就是更准确的梯度预估，选择\(f\)函数在\(\theta -\varepsilon\)上的这个点，用这个较大三角形的高比上宽，技术上的原因就不详细解释了，较大三角形的高宽比值更接近于\(\theta\)的导数，把右上角的三角形下移，好像有了两个三角形，右上角有一个，左下角有一个，通过这个绿色大三角形同时考虑了这两个小三角形。所以得到的不是一个单边公差而是一个双边公差。

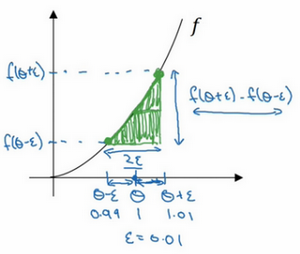
写一下数据算式，图中绿色三角形上边的点的值是\(f( \theta +\varepsilon )\)，下边的点是\(f( \theta-\varepsilon)\)，这个三角形的高度是\(f( \theta +\varepsilon)-f(\theta -\varepsilon)\)，这两个宽度都是ε，所以三角形的宽度是\(2\varepsilon\)，高宽比值为\(\frac{f(\theta + \varepsilon ) - (\theta -\varepsilon)}{2\varepsilon}\)，它的期望值接近\(g( \theta)\)，\(f( \theta)=\theta^{3}\)传入参数值，\(\frac {f\left( \theta + \varepsilon \right) - f(\theta -\varepsilon)}{2\varepsilon} = \frac{{(1.01)}^{3} - {(0.99)}^{3}}{2 \times0.01}\)，大家可以暂停视频，用计算器算算结果，结果应该是3.0001，而当\(\theta =1\)时，\(g( \theta)=3\theta^{2} =3\)，所以这两个\(g(\theta)\)值非常接近，逼近误差为0.0001，前面只考虑了单边公差，即从\(\theta\)到\(\theta +\varepsilon\)之间的误差，\(g( \theta)\)的值为3.0301，逼近误差是0.03，不是0.0001，所以使用双边误差的方法更逼近导数，其结果接近于3，现在更加确信，\(g( \theta)\)可能是\(f\)导数的正确实现，在梯度检验和反向传播中使用该方法时，最终，它与运行两次单边公差的速度一样，实际上，认为这种方法还是非常值得使用的，因为它的结果更准确。

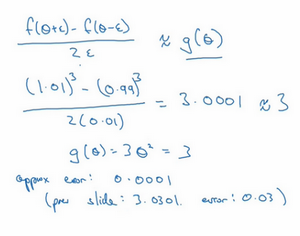
这是一些可能比较熟悉的微积分的理论，如果不太明白讲的这些理论也没关系，导数的官方定义是针对值很小的\(\varepsilon\)，导数的官方定义是\(f^{'}\theta) = \operatorname{}\frac{f( \theta + \varepsilon) -f(\theta -\varepsilon)}{2\varepsilon}\)，这里有涉及到微积分的知识。

对于一个非零的\(\varepsilon\)，它的逼近误差可以写成\(O(\varepsilon^{2})\)，ε值非常小，如果\(\varepsilon=0.01\)，\(\varepsilon^{2}=0.0001\)，大写符号\(O\)的含义是指逼近误差其实是一些常量乘以\(\varepsilon^{2}\)，但它的确是很准确的逼近误差，所以大写\(O\)的常量有时是1。然而，如果用另外一个公式逼近误差就是\(O(\varepsilon)\)，当\(\varepsilon\)小于1时，实际上\(\varepsilon\)比\(\varepsilon^{2}\)大很多，所以这个公式近似值远没有左边公式的准确，所以在执行梯度检验时，使用双边误差，即\(\frac{f\left(\theta + \varepsilon \right) - f(\theta -\varepsilon)}{2\varepsilon}\)，而不使用单边公差，因为它不够准确。

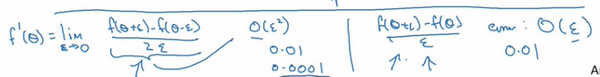
如果不理解上面两条结论，所有公式都在这儿，不用担心，如果对微积分和数值逼近有所了解，这些信息已经足够多了，重点是要记住，双边误差公式的结果更准确。

这篇讲了如何使用双边误差来判断别人给的函数\(g( \theta)\)，是否正确实现了函数\(f\)的偏导，现在可以使用这个方法来检验反向传播是否得以正确实施，如果不正确，它可能有bug需要来解决。