GJK算法：两个凸集的碰撞测试

  GJK算法用于判断两个凸集是否相交，其中GJK是三个提出者的姓名首字母。为了便于理解（偷懒），下面的内容都只在二维平面内讨论。

1. 回顾凸集

  可能有很多小伙伴忘了什么是凸集。凸集有很多等价的定义，最常用的一种是在集合中任取两点，连接这两点的线段一定在此集合内。常见的形状，例如三角形、矩形、圆、椭圆，都是凸集。

  对于两个凸集A, B, 从集合A, B中分别任取一点a, b, 所有可能的a+b构成的集合称为A与B的闵可夫斯基和，记作A+B. A+B也是一个凸集，这一点用定义很容易证明。

A+B大概长什么样子呢？假设在原点有一支铅笔，现在用一根铁棒将铅笔与集合B连接，使得它们的相对位置不发生改变。之后用铅笔将集合A涂一遍，在此过程中B扫过的区域就是集合A+B了。

  类似于加法的定义，我们可以定义A与B的闵可夫斯基差A-B: 从A, B中分别任取一点a, b, 所有可能的a-b构成的集合便是A-B. A-B也是个凸集，因为集合-B是B中所有点的坐标取反，相当于相对于原点做了个对称变换，自身的形态并没有改变，只是在空间所处的位置发生了变化，从而-B也是个凸集，因此A-B = A + (-B), 两个凸集的和当然是凸集。

  好了，到这里可以简单介绍下GJK算法的思想了：对于两个凸集A, B，想一想，如果A, B相交，那么必然有某个点同时包含在A与B中，从而凸集A-B必然包含原点；反之，如果A, B不相交，那么A-B必然不包含原点。因此，GJK算法的本质就是判断原点是否包含在A-B中。当然，GJK算法不会直接计算出A-B, 因为这样的操作在实际中不具有可操作性；对于我们讨论的二维平面，GJK算法会在A-B内找一个三角形，并在迭代过程中不断更新三角形，让这个三角形不断接近原点。为了高效实现这个目的，需要为凸集定义一个support方法。

  在这里可以找到上述内容的一个动画演示。

2. 凸集的support方法

  support方法其实很简单：这个方法接受一个二维向量direction作为输入，返回凸集在这个方向上最远的点。接口示意如下：

class ConvexSet:
    def support(direction: Vector2d) -> Vector2d:
        ...

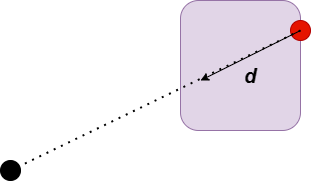
  例如，在下图中，圆在方向d₁上最远的点是图中标红的点，矩形在方向d₂上最远的点是图中标绿的点。如何找一个凸集沿着方向d 最远的点呢？作一条与d 垂直的直线l，然后沿着d 移动，直到一个极限的状态：如果沿着d 再移动一点点，凸集将会与直线l 没有任何交点；此时凸集与直线l 的交点就是沿着方向d 最远的点。

  当然，有些凸集沿着某个方向的最远点可能不止一个，例如下图所示的矩形，整条蓝色边上的点都是沿着方向d 最远的点，这时我们任取一个就好。

  既然说到这里，就顺便说说support操作是用来做什么的，这与凸集的另一个性质相关。对于这里讨论的二维平面来说，这个性质说的是，对于凸集边界上的任意一点s，都存在过s 的一条直线，使得整个凸集都在这条直线的同一侧。这个性质在这里就不证了，有兴趣的朋友可以搜索“支撑超平面”。

  给定方向d, support方法找到凸集沿着此方向最远的一个点s（不难看出，s 在凸集的边界上），此时过点s 且与方向d 垂直的直线就可以将整个凸集划分到直线的一侧（可以看看上面的示意图）；如果此时原点在直线的另一侧，就说明原点必然不包含在凸集中。

3. GJK算法

  假设输入的两个凸集为A和B, GJK算法的描述如下：

1. 1. 随机选择一个初始方向d.
   2. 计算A沿着方向d 最远的点p_a 以及B沿着方向-d (注意，这里是-d )最远的点p_b.令p = p_a - p_{b .}
   3. 令S={ p }, 更新方向d =-p.
   4. 计算A沿着方向d 最远的点p_a 以及B沿着方向-d 最远的点p_b ,令p = p_a - p_b.
   5. 如果p 与d 的点乘小于0, 则A, B不相交, 返回false.
   6. 否则, 将p 添加到集合S中.
   7. 如果S包含原点, 则A, B相交, 返回true.

  否则，从S中选择距离原点最近的一条边, 更新方向d =这条边指向原点的方向，并跳转到第4步.

二维平面的一个点既可以看作是一个点，又可以看作是原点指向这一点的向量。因此，上述中出现的 -p 实际上指的是从点 p 指向原点的向量。

4. GJK算法的解读

  前面说过，给定凸集A, B, GJK算法就是判断凸集A-B是否包含原点，只是它没有显式计算出A-B. 下面就来说明GJK算法的每一步都做了些什么。

  我们没有必要知道A-B长什么样子，只要知道它是个凸集就够了。为了说明，可以想象下A-B的样子，比如说，A-B可能长成下面这样：

  注意到GJK算法的一个关键操作：对于方向d, 计算p = A.support(d) - B.supoort(-d). 此时p 必然是A-B沿着方向d 最远的一个点。为什么？想一想，A.support(d)是A沿着方向d 最远的一个点，而B.support(-d)是B沿着方向-d 最远的一个点，考虑集合A-B的定义，还能在方向d 上找到一个更远的点吗？

例1：A与B不相交

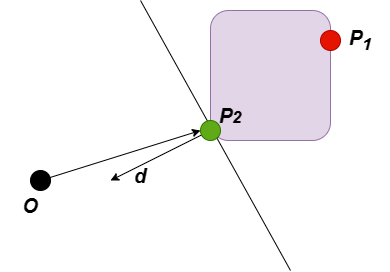
  GJK算法的第一步，随机选择一个方向，例如(1, 0), 然后计算出A.support((1, 0)) - B.supoort((-1, 0))（即凸集A-B中沿着(1, 0)最远的一个点，下图中标红的点，记作P₁）。下一步，将标红的点加入点集S, 并更新方向d 为标红的点指向原点（图中标黑的点）。

  下一步，计算A.support(d) - B.supoort(-d)， 这个点位于下图中标绿的点，我们将这个点记作P_2. 可以看到，此时向量OP₂ 与d 的夹角大于90°，因此它们的点乘小于0. 从而说明原点O不可能在A-B中，从而可以判断A与B不相交。

例2：A与B相交

  这种情况下，原点O在A-B的内部，前面的步骤同上。不过，此时向量OP₂ 与d 的点乘大于0, 如下图所示。

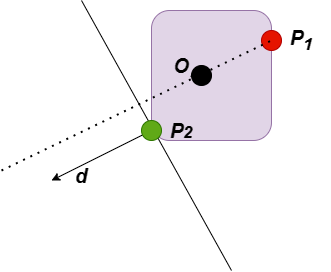
  下一步，将P₂ 加入点集S. 此时S中只有两个点，直线P₁P₂ 显然不包含原点O. 下一步更新d为P₁P₂ 指向O的方向，如下图所示：

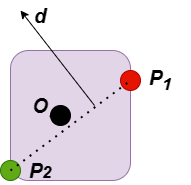
  更新d 之后，就开始了下一次的循环，计算A.support(d) - B.supoort(-d)， 这个点位于下图中标蓝的点，记作P_3. 如下图所示：

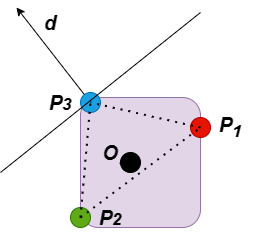
  此时向量OP₃ 与d 的点乘仍然大于0. 下一步，P₁P₂P₃ 构成的三角形已经包含原点O. 从而说明A-B包含原点O, 即A, B相交。

例3：A与B相交

  如果在例2中，P₁P₂P₃ 构成的三角形并不包含原点O. 这时就需要找到此三角形中与原点O 最近的那条边，更新点集S为这条边的两个顶点，接下来的步骤和例2中的相同：更新方向d 为这条边指向原点的方向，然后继续循环下去。（用上面的图不太好画这种情况的例子，我就不画了，改用口头叙述）

4. 小结

  可以看到，GJK算法所做的，就是用一个三角形来近似两个凸集A,B的差A-B, 然后更新这个三角形使之不断接近原点。 GJK算法的泛化性也很强，如果对于不同类型的物体，每两个类型都要写一个碰撞检测算法，比如说圆与矩形、矩形与正六边形，那得写多少?！反而，GJK算法只要求物体是凸的，而且只要提供support方法就好。而且GJK算法的收敛速度看起来也很快，不过现在我还没有想清楚为什么收敛这么快，知道原因的朋友可以在评论区交流下。

碎碎念：算法看起来不难，用Python实现了下，我的感受是一步一个坑。很多细节都需要考虑，例如如何判断原点是否在三角形内部、如何找到三角形距离原点最近的边等等。事实上，最后出现bug的地方在二维向量类的实现，有个重载运算符的地方写错了调试了好久，下次这种就用现成的类吧。