CEOI2022

Day1 T1 Abracadabra

题意：给你一个 \(1 \sim n\) 的排列 \(p\)，保证 \(n\) 为偶数，我们对它进行足够多次数的洗牌操作，定义一次洗牌为：

• 考虑取出 \(p_{1 \sim \frac{n}{2}}\) 作为序列 \(A\)，取出 \(p_{\frac{n}{2} + 1 \sim n}\) 作为序列 \(B\)，将 \(A\) 和 \(B\) 归并后重新放回 \(p\)，其中归并表示每次取两个序列第一个数的较小值。

给出 \(q\) 次询问，每次询问给出 \(t, x\)，求 \(t\) 次洗牌后的 \(p_x\) 是多少。

\(n \times 2 \times 10^5, q \le 10^6, t \le 10^9\)。

直接维护洗牌过程肯定时不可行的，所以我们需要发掘一些关于洗牌的性质。

考虑 \(A\) 或 \(B\) 中（我们钦定为 \(A\)）一个长度为 \(2\) 的连续子序列 \(A_{i \sim i + 1}\)，满足 \(A_i > A_{i + 1}\)，那么在归并时只要加入 \(A_i\) 必定加入 \(A_{i + 1}\)，所以我们套路的将 \(A_i\) 和 \(A_{i + 1}\) 绑定。

现在拓展一下，我们分别考虑 \(A\) 和 \(B\) 的单调栈，单调栈中每一个元素是序列中的前缀最大值。序列被这些元素划分成了若干连续段，每一段有一个性质是”选了这个段的第一个元素就必须选整个段“。我们从段的角度考虑，发现它的第一个值决定整个段被选的时间，我们称其为关键元，我们发现在 \(A\) 和 \(B\) 两个序列上关键元分别是单调递增的。

但是维护 \(A\) 和 \(B\) 上的连续段显然是困难的，因为它们会归并到 \(p\)。我们考虑维护 \(p\) 上的连续段，每次洗牌会从 \(\frac{n}{2} \sim \frac{n}{2} + 1\) 处截断，如果截断的地方没有连续段，那么操作直接结束，因为 \(A\) 和 \(B\) 都是已经归并完的，继续归并又会得到原序列。

否则一定存在一个连续段在 \(\frac{n}{2} \sim \frac{n}{2} + 1\) 处被截断，此时这个连续段被分成了两部分，\(\frac{n}{2}\) 之前的部分归属于 \(A\)，\(\frac{n}{2} + 1\) 之后的部分归属于 \(B\)，考虑 \(A\) 部分的连续段不会发生变化，\(B\) 部分相当于对一个连续段的后缀独立了，需要重构。

注意到一个非常重要的性质，就是任意时刻的任意一个连续段是原序列上的一段区间，因为我们只分裂的连续段而没有合并，所以重构时可以在原序列上找后面第一个大于自己的数，单调栈即可。由于操作之间不独立，连续段最多分裂 \(n - 1\) 次，所以我们可以暴力跳后继，每跳一次段数 \(+1\)，同时也说明了有效洗牌树不超过 \(n - 1\)，\(t\) 可以对 \(n - 1\) 取 \(\min\)，使得我们只需维护前 \(n - 1\) 次操作。

然后我们需要找中点和找某一时刻的第 \(i\) 个数，线段树二分即可，时间复杂度 \(O((n + q) \log n)\)。

Code

#include <iostream>
#include <deque>
#include <vector>
#include <queue>
#include <stack>

#define lc (k << 1)
#define rc ((k << 1) | 1)

using namespace std;

const int N = 2e5 + 5, T = N * 4, Q = 1e6 + 5; 

int n, q, a[N], p[N], siz[N], nx[N];
int ans[Q];
vector<pair<int, int>> qr[N];
int cnt[T];

void Add (int k, int x, int y, int L = 1, int R = n) {
  cnt[k] += y;
  if (L == R) return;
  int mid = (L + R) >> 1;
  if (x <= mid)
    Add(lc, x, y, L, mid);
  else
    Add(rc, x, y, mid + 1, R);
}

int Query (int k, int &x, int L = 1, int R = n) {
  if (L == R) return L;
  int mid = (L + R) >> 1;
  if (x <= cnt[lc])
    return Query(lc, x, L, mid);
  else
    return Query(rc, x -= cnt[lc], mid + 1, R);
}

int Next (int x) {
  for (int i = x; i <= n; ++i) {
    if (a[i] > a[x])
      return i;
  }
  return n + 1;
}

void Print () {
  bool fl = 0;
  for (int i = 1; i <= n; ++i) {
    if (!siz[i]) continue;
    if (fl) cout << "| ";
    fl = 1;
    for (int j = p[i]; j < p[i] + siz[i]; ++j) {
      cout << a[j] << ' ';
    }
  }
  cout << '\n';
}

int main () {
  // freopen("abracadabra.in", "r", stdin);
  // freopen("abracadabra.out", "w", stdout);
  cin.tie(0)->sync_with_stdio(0);
  cin >> n >> q;
  int la = 0, cur = 0;
  for (int i = 1; i <= n; ++i) {
    cin >> a[i], p[a[i]] = i;
    if (a[i] > cur)
      cur = a[i];
    ++siz[cur];
  }
  stack<int> s;
  fill(nx + 1, nx + n + 1, n + 1);
  for (int i = 1; i <= n; ++i) {
    while (!s.empty() && a[i] > a[s.top()]) {
      nx[s.top()] = i, s.pop();
    }
    s.push(i);
  }
  for (int i = 1, t, x; i <= q; ++i) {
    cin >> t >> x, t = min(t, n - 1);
    qr[t].push_back({x, i});
  }
  for (int i = 1; i <= n; ++i) {
    Add(1, i, siz[i]);
  }
  // Print();
  for (int t = 1; t <= n; ++t) {
    for (auto i : qr[t - 1]) {
      int j = Query(1, i.first);
      ans[i.second] = a[p[j] + i.first - 1];
    }
    int tmp = n / 2, j = Query(1, tmp);
    if (siz[j] == tmp) continue;
    int k = p[j] + tmp, ed = p[j] + siz[j] - 1;
    Add(1, j, tmp - siz[j]), siz[j] = tmp;
    for (int r = k; r <= ed; r = nx[r]) {
      Add(1, a[r], siz[a[r]] = min(ed + 1, nx[r]) - r);
    }
    // Print();
  }
  for (int i = 1; i <= q; ++i) {
    cout << ans[i] << '\n';
  }
  return 0;
}

Day1 T2 Homework

题意：有一个由若干个 \(\max\) 和 \(\min\) 组成的表达式，其中有 \(n\) 个变量 \(x_{1 \sim n}\)，它们全部未知（比如 \(\texttt{min(min(?,?),min(?,?))}\)）。

现在你可以任意将这些变量赋值为一个 \(1 \sim n\) 的排列，求最终表达式的值有多少种可能。

\(n\le 10^6\)。

考虑计算表达式的过程形如一棵二叉树，二叉树上的叶子是一个变量，非叶子结点是 \(\max\) 和 \(\min\) 运算中的一个。

注意到答案可以表示为一段区间 \([l, r]\)，在 \([l, r]\) 以外的全部不合法。这个很好理解，因为一个 \(\max\) 只会删掉一段前缀，一个 \(\min\) 只会删掉一段后缀。我们考虑求出 \(l, r\)，答案记为 \(r - l + 1\)。

我们直接在这颗二叉树上 \(\text{dp}\)，设 \(f_i\) 表示 \(i\) 子树内表达式的最小值，\(g_i\) 表示 \(i\) 子树内表达式的最大值，相当于对于每一棵子树，我们都维护了一个区间 \([l, r]\)。

考虑转移。以 \(f\) 为例，\(g\) 是镜像的过程：

• 如果当前结点 \(i\) 上运算为 \(\min\)，那么 \(f_i = \min(f_{lc}, f_{rc})\)，表示我们考察其两个子树 \(lc, rc\)，选 \(f\) 值小的那个儿子，将 \(1 \sim f\) 中的所有数全部塞到这个儿子里，取 \(\min\) 后相当于可以继承这个较小的 \(f\)。

• 如果当前结点 \(i\) 上运算为 \(\max\)，那么 \(f_i = f_{lc} + f_{rc}\)。表示我们对于两个儿子的 \(1 \sim f\) 分别塞满，但是一个数不能用两次，所以应将两棵子树中需要的数的个数相加。

时间复杂度 \(O(n)\)。

Code

#include <iostream>
#include <stack>

using namespace std;

const int N = 1e6 + 5; 

int n, tot, f[N], g[N];
stack<int> ns, os; 

int main () {
  cin.tie(0)->sync_with_stdio(0);
  string s;
  cin >> s;
  for (auto c : s)
    n += c == '?';
  for (int i = 0; i < s.size(); ++i) {
    if (s[i] == 'm') {
      os.push(s[i + 1] == 'a');
    }
    else if (s[i] == '?') {
      ++tot, f[tot] = 1, g[tot] = n;
      ns.push(tot);
    }
    else if (s[i] == ')') {
      int v = ns.top();
      ns.pop();
      int u = ns.top();
      if (!os.top()) {
        f[u] = min(f[u], f[v]);
        g[u] = g[u] + g[v] - n - 1;
      }
      else {
        f[u] = f[u] + f[v];
        g[u] = max(g[u], g[v]);
      }
      os.pop();
    }
  }
  cout << g[1] - f[1] + 1 << '\n';
  return 0;
}

Day1 T3 Prize

题意：给出两棵树 \(T_0, T_1\) 的形态，边有边权，但是你在初始时刻并不知道。给出参数 \(k\)（\(k\) 由交互库任意选择），首先你需要选择一个大小为 \(k\) 的点集 \(S\)。

然后你可以进行 \(k - 1\) 询问，每次你可以给出两个点 \(u, v\)，设 \(w_0\) 为 \(u\) 和 \(v\) 在 \(T_0\) 上的 \(\text{LCA}\)，\(w_1\) 为 \(u\) 和 \(v\) 在 \(T_1\) 上的 \(\text{LCA}\)，\(dis_i(u, v)\) 为 \(u\) 和 \(v\) 在 \(T_i\) 上的距离，交互库会给出 \(dis_0(u, w_0), dis_0(v, w_0), dis_1(u, w_1), dis_1(v, w_1)\)。

接下来交互库会进行 \(t\) 次询问，每次询问给出两个数 \(u, v \in S\)，你需要回答 \(dis_0(u, v), dis_1(u, v)\)。

\(n \le 10^6, k \le 10^3, t \le 10^5\)。

首先将题意转化一步，考虑你需要获取什么信息，才能回答交互库提出的询问。容易发现，对于 \(S\) 建虚树后，你需要知道虚树上任意点对的深度差。回答 \((u, v)\) 的询问时，由于树的形态确定，求一下 \(\text{LCA}\) 为 \(w\)，答案就是 \((dep_u - dep_w) + (dep_v - dep_w)\)。这里的深度指的都是一个点到根的距离。

考虑为什么在 \(S\) 为任意点集时不可做。此时你有一种类似于每次询问两个编号相邻的点的策略，但是你的询问可能无法覆盖所有虚树上的点，比如下面的情况：

注意这里所说的编号相邻只是策略之一。比如你可以在 \(T_0\) 上可以选择一些有性质的点，但它们在 \(T_1\) 上可能什么性质也没有。所以我们知道任意询问 \(k - 1\) 个点对肯定是不行的。并且你可以任意选定 \(S\) 的这个条件一定有用。

考虑只有一棵树，但是任意给出一个 \(S\) 的情况，此时你可以用 \(k - 1\) 次询问模拟二次排序建虚树的过程，每次询问一对 \(dfn\) 相邻的点，那么你可以将虚树上的所有点覆盖。

那么接下来的做法就很显然了，考虑用任意选定 \(S\) 的方法解决 \(T_0\) 的限制，用模拟建虚树的方法解决 \(T_1\) 的限制。

一种方法是选定 \(S\) 时选择 \(T_0\) 上 \(\text{dfs}\) 序的一段前缀，这样可以保证 \(S\) 的虚树是其本身（\(\text{dfs}\) 序上的一段前缀一定满足儿子被选则父亲也被选，模拟任意选两个点跳 \(\text{LCA}\) 的过程可说明封闭性）。询问时将所有 \(S\) 中的点按 \(T_1\) 上的 \(dfn\) 排序，每次询问相邻的点对即可。此时再考虑 \(T_0\)，\(k - 1\) 次询又至少构成了一棵树，此时我们任意钦定一个点的深度并 \(\text{dfs}\)，即可求出所有点的相对深度。

时间复杂度 \(O((n + t) \log n)\)。

Code

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

const int N = 1e6 + 5, M = 20;

int n, k, q, t; 

struct Tree {
  int rt, tot, vr;
  vector<int> e[N], v, pv;
  vector<pair<int, int>> t[N];
  int dfn[N], rmp[N], fa[N][M], dep[N], pre[N];
  bool vis[N];

  void Dfs (int u) {
    dep[u] = dep[fa[u][0]] + 1;
    rmp[dfn[u] = ++tot] = u;
    for (auto v : e[u]) {
      fa[v][0] = u, Dfs(v);
    }
  }

  void Build () {
    for (int i = 1, f; i <= n; ++i) {
      cin >> f;
      if (f != -1) {
        e[f].push_back(i);
      }
      else {
        rt = i;
      }
    }
    Dfs(rt);
    for (int k = 1; k < M; ++k) {
      for (int i = 1; i <= n; ++i) {
        fa[i][k] = fa[fa[i][k - 1]][k - 1];
      }
    }
  }

  int Lca (int u, int v) {
    if (dep[u] < dep[v])
      swap(u, v);
    for (int k = M - 1; ~k; --k) {
      if (dep[u] - dep[v] >= (1 << k)) {
        u = fa[u][k];
      }
    }
    if (u == v) return u;
    for (int k = M - 1; ~k; --k) {
      if (fa[u][k] != fa[v][k])
        u = fa[u][k], v = fa[v][k];
    }
    return fa[u][0];
  } 

  void Build_virtual (vector<int> _v) {
    v = _v;
    auto cmp = [&](int i, int j) -> bool {
      return dfn[i] < dfn[j];
    };
    sort(v.begin(), v.end(), cmp), pv = v;
    for (int l = v.size(), i = 0; i < l - 1; ++i) {
      v.push_back(Lca(v[i], v[i + 1]));
    }
    sort(v.begin(), v.end(), cmp);
    v.resize(unique(v.begin(), v.end()) - v.begin()), vr = v[0];
  }

  void Add_limit (int u, int v, int x, int y) {
    int w = Lca(u, v);
    t[w].push_back({u, x});
    t[u].push_back({w, -x});
    t[w].push_back({v, y});
    t[v].push_back({w, -y});
  }

  void Calc (int u) {
    vis[u] = 1;
    for (auto i : t[u]) {
      int v = i.first, w = i.second;
      if (vis[v]) continue;
      pre[v] = pre[u] + w, Calc(v);
    }
  } 

  int Get_dis (int u, int v) {
    int w = Lca(u, v);
    return pre[u] + pre[v] - pre[w] * 2;
  }
} tr[2]; 

int main () {
  cin >> n >> k >> q >> t;
  tr[0].Build(), tr[1].Build();
  vector<int> v;
  for (int i = 1; i <= k; ++i) {
    v.push_back(tr[0].rmp[i]);
  }
  for (auto i : v) {
    cout << i << ' ';
  }
  cout << endl;
  tr[0].Build_virtual(v), tr[1].Build_virtual(v);
  for (int i = 0; i < k - 1; ++i) {
    int u = tr[1].pv[i], v = tr[1].pv[i + 1];
    cout << "? " << u << ' ' << v << endl;
  }
  cout << "!" << endl;
  for (int i = 0; i < k - 1; ++i) {
    int u = tr[1].pv[i], v = tr[1].pv[i + 1], x[2], y[2];
    cin >> x[0] >> y[0] >> x[1] >> y[1];
    tr[0].Add_limit(u, v, x[0], y[0]), tr[1].Add_limit(u, v, x[1], y[1]);
  }
  tr[0].Calc(tr[0].vr), tr[1].Calc(tr[1].vr);
  vector<pair<int, int>> qr(t);
  for (auto &q : qr)
    cin >> q.first >> q.second;
  for (auto q : qr) {
    cout << tr[0].Get_dis(q.first, q.second) << ' ' << tr[1].Get_dis(q.first, q.second) << '\n';
  }
  return 0;
}

Day2 T1 Drawing

题意：给定平面上的 \(n\) 个点，和一棵 \(n\) 个结点的二叉树。你需要将平面上的点（Point）和树上的结点（Node）一一对应，使得平面上的点按照树的形态连接后，任意两条线段在除端点处无交。

\(1 \le n \le 2 \times 10^5\)。

先考虑一个较为直接的做法：

• 我们在树上随便钦定一个点为根，再随便钦定一个根的对应点，然后以该点为原点，将平面上所有点极角排序。将每一个子树对应一段极角序连续的点，递归地做下去即可。

我们发现这种做法在随机数据下是比较优秀的，但当树是一条链时，时间复杂度为 \(O(n^2)\)。可以考虑用点分治优化，但是点分治的要求是每一层任意钦定子树的根，这样你才能找重心。但是这题任意钦定子树根显然是有问题的，它可能会使根-子树根的边，和子树内的边产生冲突。

于是我们考虑链分治（提前说明，我下面说的链分治和大众做法和官方题解并不一样，请谨慎使用）：

还是在树上任意钦定一个根 \(a\)，任意找一个凸包上的点 \(A\) 为对应点，考虑沿将 \(a\) 所在的重链拎出来，记链首为 \(a\)，那么链尾为 \(b\)，将 \(b\) 的对应点钦定为 \(A\) 在凸包上的一个相邻点 \(B\)，然后我们需要在这条重链上分治。

找到树链 \(a \rightarrow b\) 的中点 \(c\)，考虑将问题分解为 \(c\) 子树内的部分和 \(c\) 子树外的部分（两部分都包括 \(c\)）分别求解，假设第一个问题结点数为 \(n_1\)，第二个问题结点数为 \(n_2\)。

接下来我们需要找一个 \(c\) 的对应点 \(C\)，我们希望分解出来的两个问题互不干扰，以便我们分别独立求解。考虑构造一种方式，使得 \(\triangle ABC\) 中没有点。我们将所有点按照 \(A\) 极角排序，取出前 \(n_2\) 个点，在找一个关于 \(B\) 极角序最大的点，我们钦定该点为 \(C\)。

确定了 \(C\) 以后，我们再以 \(C\) 为原点极角排序，取前 \(n_2\) 个点划分到子问题 \(2\)，其余的点划分到子问题 \(1\)。下面是一张做工粗糙的图：

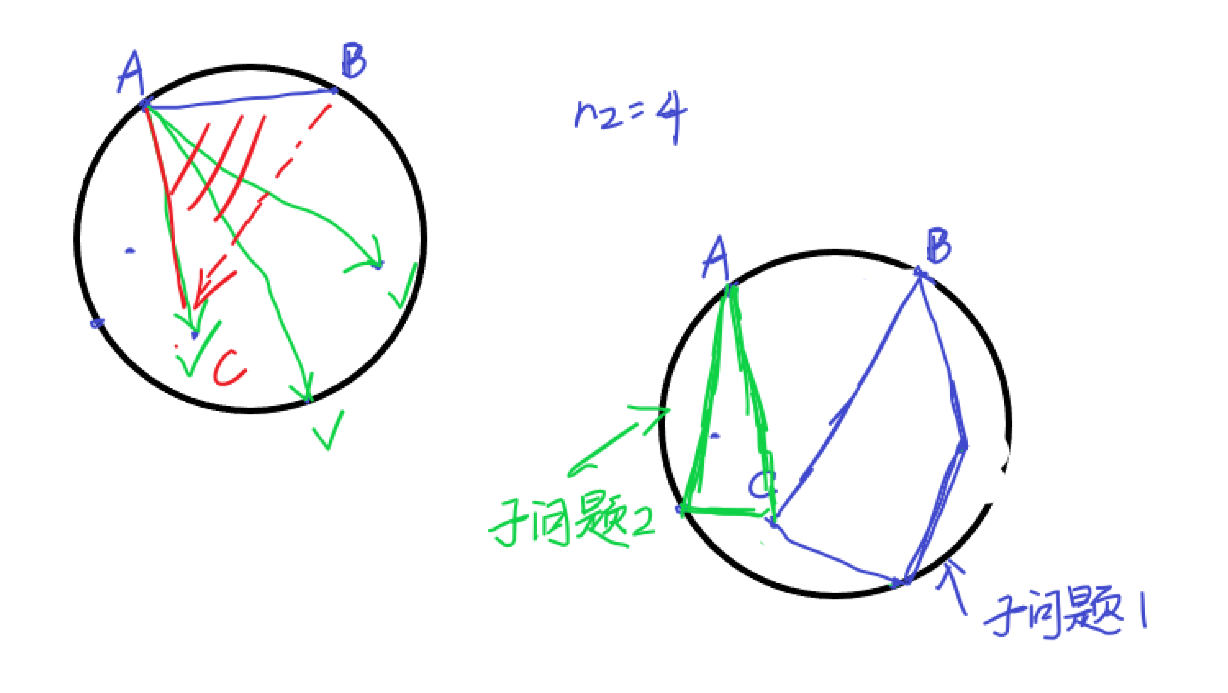
留下的两个子问题，递归求解即可。我们容易发现 \(AC\) 和 \(BC\) 分别是两个点集的凸包上的一条边，那么考虑我们最后一定将所有点划分成若干个凸包，这些凸包的求解相互独立，互不相交，而每条树边都是凸包上的一条边，所以这样做是对的。

可能在树上有若干 Corner Case，比如钦定的重链只剩下两个点 \(a\) 和 \(b\)，此时找不到中点，但是对应点 \(A\) 和 \(B\) 都已经确定，此时直接将边 \((a, b)\) 割掉，在 \(a\) 子树内重新钦定一条重链即可。下图是链分治在树上的形态：

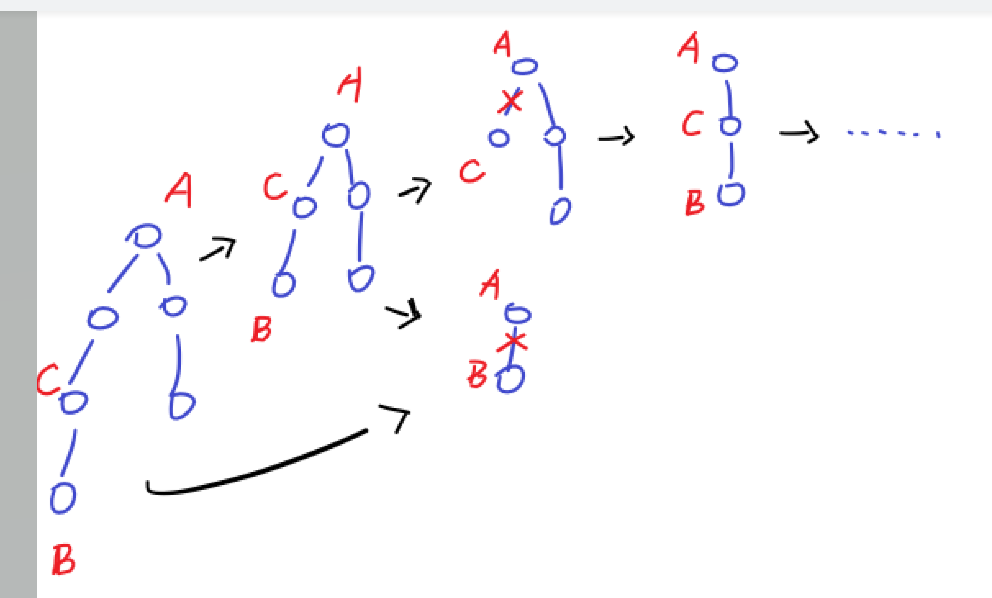
以上所谓极角排序其实并不用排序，只需要找前 \(k\) 小即可。可以考虑用 \(\text{nth_element}\)，或者手写一个类似快速排序的东西，时间复杂度是线性的，考虑每递归到一个子问题，设点数为 \(n\)，则在该层的时间复杂度为 \(O(n)\)。

下面分析时间复杂度，考虑按照子问题不好分析，可以按照重链分析，每次相当于消掉一条重链。设原问题规模为 \(n\)，在对这一条重链分治的过程中，由于是每次取中点，所以只有每个点只会在 \(O(\log n)\) 个子问题中出现，这一部分时间复杂度为 \(O(n \log n)\)。

考虑还分解出若干子问题，规模分别为 \(n_1, n_2, \ldots, n_k\)，这些子问题必然经过一条轻边，由于原树是二叉树，那么经过一条轻边规模必然减半（其实是我实现的问题，如果实现的好一点不是二叉树也可做），那么 \(\forall i \in [1, k], n_i \le \frac{n}{2}\)，我们可以得到递归式 \(T(n) = \sum\limits_{i = 1}^{k} T(n_i) + O(n \log n)\)，通过主定理或者建递归树容易分析出 \(T(n) = O(n \log^2 n)\)。

代码非常难写。对于凸包退化（三点共线）的情况请慎重考虑！对于极角排序时极角相同的情况，在哪个部分是优先较近点，哪个部分是优先较远点，请慎重考虑！

Code

#include <iostream>
#include <vector>
#include <map>
#include <algorithm>
#include <cassert>

using namespace std;
using LL = long long;
using Pii = pair<int, int>; 

Pii operator- (Pii a, Pii b) {
  return {a.first - b.first, a.second - b.second};
}

LL operator* (Pii a, Pii b) {
  return 1ll * a.first * b.second - 1ll * a.second * b.first;
}

LL Cross (Pii a, Pii b, Pii c) {
  return (a - c) * (b - c);
}

LL Dis (Pii a) {
  return 1ll * a.first * a.first + 1ll * a.second * a.second;
}

struct Polar_Angle {
  Pii O;
  int type, type2;
  // type = 0 : closer is better
  // type = 1 : further is better
  // type2 = 0 : return more left-hand element
  // type2 = 1 : return more right-hand element
  vector<pair<Pii, bool>> lim; 

  Polar_Angle (Pii O, int type, vector<pair<Pii, bool>> lim, int type2 = 0) : O(O), type(type), lim(lim), type2(type2) {}

  bool operator() (Pii a, Pii b) {
    for (auto i : lim) {
      if (i.first == a) return i.second;
      if (i.first == b) return !i.second;
    }
    LL ret = Cross(a, b, O);
    if (ret != 0) return (ret < 0) ^ type2;
    return (Dis(a - O) < Dis(b - O)) ^ type;
  }
}; 

const int N = 2e5 + 5;

int n;
vector<int> e[N];
Pii pv[N];
map<Pii, int> mp;
int lc[N], rc[N], fa[N], ans[N], siz[N];

void Dfs (int u) {
  for (auto v : e[u]) {
    if (v == fa[u]) continue;
    int &child = (!lc[u] ? lc[u] : rc[u]);
    fa[v] = u, Dfs(child = v);
  }
}

void Connect (int a, Pii A) {
  ans[mp[A]] = a;
}

void Solve (Pii *be, Pii *ed, int a, Pii A);
void Solve (Pii *be, Pii *ed, int a, Pii A, int b, Pii B);

void Rebuild (int u) {
  siz[u] = 1;
  if (lc[u]) {
    Rebuild(lc[u]);
    siz[u] += siz[lc[u]];
  }
  if (rc[u]) {
    Rebuild(rc[u]);
    siz[u] += siz[rc[u]];
  }
}

void Solve (Pii *be, Pii *ed, int a, Pii A) {
  if (!lc[a] && !rc[a]) return;
  Rebuild(a);
  int b = a;
  while (lc[b] || rc[b]) {
    b = (siz[lc[b]] > siz[rc[b]] ? lc[b] : rc[b]);
  }
  Polar_Angle cmp(A, 1, {});
  Pii B;
  bool fl = 0;
  for (Pii *i = be; i != ed; ++i) {
    Pii p = *i;
    if (p == A) continue;
    if (!fl) {
      fl = 1, B = p;
    }
    else if (cmp(p, B)) {
      B = p;
    }
  }
  Connect(b, B);
  Solve(be, ed, a, A, b, B);
}

int Get_midpoint (int a, int b) {
  int c = b;
  while (c != a) {
    c = fa[c];
    if (c == a) return b;
    c = fa[c];
    b = fa[b];
  }
  return b;
}

void Cut (int a, int b) {
  fa[b] = 0;
  (b == lc[a] ? lc[a] : rc[a]) = 0;
}

void Solve (Pii *be, Pii *ed, int a, Pii A, int b, Pii B) {
  int n = ed - be, c = Get_midpoint(a, b);
  if (c == b) {
    Pii *pos = find(be, ed, B);
    for (Pii *i = pos; i != be; --i) {
      swap(*i, *(i - 1));
    }
    Cut(a, b);
    Solve(be + 1, ed, a, A);
    return;
  }
  Rebuild(a);
  Polar_Angle cmp(A, 1, {{B, 1}, {A, 0}});
  int n2 = siz[c], n1 = n - siz[c] + 1;
  Pii *mid = be + n2;
  auto tval = [&](Pii a) -> int {
    bool fl = !Cross(a, A, B) && Dis(a - B) > Dis(A - B);
    return !fl;
  };
  auto tcmp = [&](Pii a, Pii b) -> bool {
    if (tval(a) != tval(b))
      return tval(a) > tval(b);
    return cmp(a, b);
  };
  nth_element(be, mid, ed, tcmp);
  Polar_Angle cmp2(B, 0, {}, 1);
  Pii C;
  bool fl = 0;
  for (Pii *i = be; i != mid; ++i) {
    Pii p = *i;
    if (p == A || p == B) continue;
    if (!fl) {
      fl = 1;
      C = p;
    }
    else if (cmp2(p, C)) {
      C = p;
    }
  }
  Connect(c, C);
  Polar_Angle cmp3(C, 0, {{A, 0}, {B, 1}, {C, 1}});
  auto sgn = [&](Pii a) -> int {
    return Cross(a, B, C) >= 0;
  };
  auto cmp4 = [&](Pii a, Pii b) -> bool {
    if (sgn(a) != sgn(b))
      return sgn(a) > sgn(b);
    return cmp3(a, b);
  };
  nth_element(be, mid, ed, cmp4);
  Solve(be, mid, c, C, b, B);
  if (lc[c]) Cut(c, lc[c]);
  if (rc[c]) Cut(c, rc[c]);
  Solve(mid - 1, ed, a, A, c, C);
}

int main () {
  // freopen("tmp.in", "r", stdin);
  // freopen("tmp.out", "w", stdout);
  cin.tie(0)->sync_with_stdio(0);
  cin >> n;
  for (int i = 1, u, v; i < n; ++i) {
    cin >> u >> v;
    e[u].push_back(v);
    e[v].push_back(u);
  }
  for (int i = 1; i <= n; ++i) {
    cin >> pv[i].first >> pv[i].second;
    mp[pv[i]] = i;
  }
  int rt = 1;
  for (int i = 1; i <= n; ++i) {
    if (e[i].size() != 3)
      rt = i;
  }
  Dfs(rt);
  sort(pv + 1, pv + n + 1);
  int sa = rt;
  Pii sA = pv[1];
  Connect(sa, sA);
  Solve(pv + 1, pv + n + 1, sa, sA);
  for (int i = 1; i <= n; ++i) {
    cout << ans[i] << ' ';
  }
  cout << '\n';
  return 0;
}

Day2 T2 Measures

题意：数轴上有 \(N\) 个人，第 \(i\) 个人的坐标为 \(a_i\)，每个人可以花费 \(1\) 单位时间移动一单位距离。

由于某些原因，它们要保持社交距离，所以它们希望任意两个人的距离至少为 \(D\)。

现在额外进行 \(M\) 次操作，每次操作加入一个位置为 \(b_i\) 的人，并且你需要求出现在加入的所有人保持社交距离的最小时间。

\(1 \le N, M \le 2 \times 10^5\)。

首先因为 \(N\) 和 \(M\) 同级，我们可以将初始存在的人也看成加入操作，这样问题会变得简单一些。我们只需考虑如何动态维护答案。

考虑静态的情况怎么做，也就是给你所有人的坐标，让你单次求出答案。设 \(A_u\) 为第 \(i\) 个人的坐标，假设我们已经对 \(A\) 从小到大排序，那么答案即为：

\[t = \max\limits_{i < j} (j - i)D - (A_j - A_i)
\]

证明考虑让每个人先向左走 \(t\) 个单位，那么每个人可以选择向右走 \([0, 2t]\) 个单位，然后每个人贪心选一个最靠左的位置，即可得到上面这个式子。

为了方便计算，我们令 \(B_i = A_i - iD\)，那么答案可以表示为：

\[\max\limits_{i < j} B_i - B_j
\]

这个东西可以考虑用线段树维护，记录答案，最大值，最小值即可。那么先将所有插入操作离线，这样插时入可以方便的定位到线段树上，另外插入时 \(B\) 会变化，它形如一段前缀 \(+D\)。不过线段树维护区间加也是方便的，我们只需额外维护一个懒标记。

时间复杂度 \(O(N \log N)\)。

Code

#include <iostream>
#include <algorithm>
#include <numeric>

#define lc (k << 1)
#define rc ((k << 1) | 1)

using namespace std;
using LL = long long;

const int N = 4e5 + 5, T = N * 4;
const LL Inf = 1e18;

int n, m, d;
int a[N], p[N], pos[N];
LL mx[T], mi[T], ans[T], tag[T];

void Insert (int k, int x, int y, int L = 1, int R = n + m) {
  if (L == R)
    return mx[k] = mi[k] = y + tag[k], void();
  int mid = (L + R) >> 1;
  if (x <= mid) {
    Insert(lc, x, y, L, mid);
  }
  else {
    mx[lc] += d, mi[lc] += d, tag[lc] += d;
    Insert(rc, x, y, mid + 1, R);
  }
  mx[k] = tag[k] + max(mx[lc], mx[rc]);
  mi[k] = tag[k] + min(mi[lc], mi[rc]);
  ans[k] = max(max(ans[lc], ans[rc]), mx[lc] - mi[rc]);
}

int main () {
  cin.tie(0)->sync_with_stdio(0);
  cin >> n >> m >> d;
  for (int i = 1; i <= n + m; ++i) {
    cin >> a[i], p[i] = a[i];
  }
  sort(p + 1, p + n + m + 1);
  fill(mx, mx + (n + m) * 4 + 1, -Inf);
  fill(mi, mi + (n + m) * 4 + 1, Inf);
  iota(pos + 1, pos + n + m + 1, 1);
  for (int i = 1; i <= n + m; ++i) {
    int t = upper_bound(p + 1, p + n + m + 1, a[i]) - p - 1;
    Insert(1, pos[t]--, a[i]);
    if (i > n) {
      cout << ans[1] / 2;
      if (ans[1] & 1) cout << ".5";
      cout << ' ';
    }
  }
  cout << '\n';
  return 0;
}

Day2 T3 Parking

题意：停车场中有 \(n\) 种颜色的车，每种颜色的车恰好有两辆，有 \(m\) 个车位，每个车位形如一个大小为 \(2\) 的栈，只能在顶部进车和出车。初始时这 \(2n\) 辆车都停放在这些车位中，车的摆放形态给定。

现在你可以进行若干次操作，每次操作你可以将一辆在车位顶部的车开到另一个车位的顶部。

求是否用一种操作方式，使得进行了这些操作后，每种颜色的两辆车都在同一个车位中。如果存在这种操作方式，你还需要最小化操作次数，并给出一种最优方案。

\(1 \le n \le m \le 2 \times 10^5\)。

由于我们的目标是对于每一种颜色，都要让该颜色的两辆车出现在同一个栈中，那么这两辆车的分布位置非常重要。考虑假设有一种颜色，它对应的两辆车一个出现在位置 \(u\)，一个出现在位置 \(v\)，若 \(u = v\)，那么它已经合法，我们一定不会操作它，可以直接忽略。否则我们连一条无向边 \((u, v)\)。

注意到每个车位至多有两辆车，里面的每辆车最多贡献 \(1\) 的度数。所以这张图满足所有点度数 \(\le 2\)，显然，它只能由若干环和链组成。这些环和链我们可以独立考虑。

先考虑较为简单的链，显然有些情况链两端可以直接匹配，此时相当于删掉了一个叶子，我们不断重复这个过程，直到所有结点被删空，或者链的两端都无法删去。

如果能够通过上述操作删空当然是简单的，但是如果不能呢？考虑此时这条链一定长成这样：

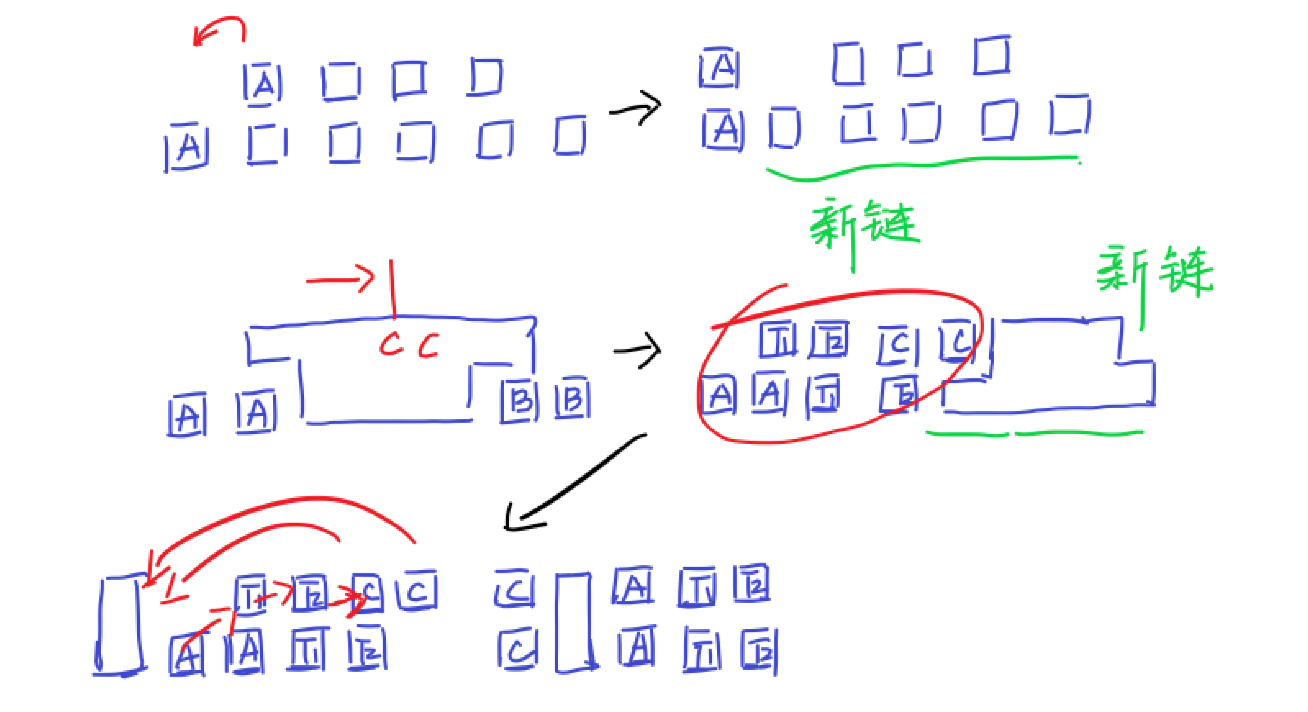
考虑下图的情况，这里我们默认将链拉成序列状，链的两端分别为 \(A\) 和 \(B\)，那么一定是两个 \(A\) 和 \(B\) 都位于车位底端，才使我们不能消去，此时你考虑除 \(A\) 和 \(B\) 外的其他元素，由于图是一条链，设位于底端的元素个数为 \(B\)，位于顶端的元素个数为 \(T\)，有 \(B = T + 2\)，由于 \(A\) 和 \(B\) 全部位于底端，那么对于其他元素有 \(B' = T' - 2\)。那么根据鸽巢原理，一定有一个元素连续在顶端出现两次，我们找到第一个这样的元素，并记它为 \(C\)。

对于 \(C\) 右端又构成了一条链，这个我们可以递归的做下去。考虑我们可以证明 \(C\) 左端（包括 \(C\)）可以全部消掉。

设 \(A\) 和 \(C\) 之间顺次排列了若干元素 \(T_1, T_2, T_k\)，具体如上图所示。我们一定需要先借用一个车位，将两个 \(C\) 全部放进去，然后从 \(T_k\) 开始，倒着将 \(T_k, T_{k - 1}, \ldots, T_2, T_1\) 归位，最后将 \(A\) 也归位，具体构造上图也画的很清楚了。

由于两个 \(A\) 是平放的，还原时又会空出一个车位。那么遇到这种情况相当于先借用一个车位，然后又可以还回来一个车位。

之后我们将看到，无论是对于链的情况，还是对于环的情况，是否存在形如两个连续车位，满足有一种颜色的车同时出现在车两个车位顶端，这样的单元非常重要，我们将其称为坏单元。

那么对于没有坏单元的链，我们可以直接消掉，并且由于这条链上原本存在两个车位只有一辆车，现在全满了，相当于可以直接提供一个车位。对于有环的链，我们需要借用一个车位才能消掉，但是类似的可以知道消完后我们将获得两个车位。

接下来考虑环，如果对链的部分完全理解的话环就比较简单了，分类讨论以下：

• 若不存在坏单元，则我们可以借用一个车位，随便将一辆位于顶端的车丢进去，剩下部分构成一个不含坏单元的链，归约到链的情况可知，我们需要先借用一个车位，消完后可以提供一个车位。

• 若存在一个坏单元，我们还是借用一个一个车位，将那两辆位于顶端的颜色相同的车丢进去，剩下部分归约到无坏单元的链，依旧是借用一个车位后提供一个车位。

• 若存在两个坏单元，我们无论怎么操作都会构成一个有坏单元的链，借用一个车位并随便丢一个进去，到了链的情况还需借用一个车位，那么我们相当于借用了两个车位后提供两个车位。

总结以下四种情况：

• 链

  • 不存在一个坏单元，我们可以直接获得一个车位。

  • 存在一个坏单元，我们需要借用一个车位并获得两个车位。

• 环

  • 存在不超过一个坏单元，我们需要借用一个车位并获得一个车位。

  • 存在至少两个坏单元，我们需要借用两个车位并获得两个车位。

那么我们拿出所有初始为空的车位，贪心维护以上过程，显然按照上面顺序从上往下做是最优的，如果某一时刻需要车位但没有车位则无解。

容易发现我们整个过程都没有做无用的操作，操作次数自然是最小的。

时间复杂度 \(O(n)\)。

Code

#include <iostream>
#include <vector>
#include <cassert>
#include <algorithm>

using namespace std;

template <typename T>
void Append (vector<T> &a, vector<T> b) {
  for (auto i : b)
    a.push_back(i);
}

const int N = 2e5 + 5;

int n, m;
int a[N][2], pa[N], pb[N];
vector<int> e[N], cur;
bool vis[N];

void Add_edge (int u, int v) {
  e[u].push_back(v);
  e[v].push_back(u);
}

void Dfs (int x) {
  vis[x] = 1;
  cur.push_back(x);
  for (auto y : e[x]) {
    if (!vis[y])
      Dfs(y);
  }
}

struct List {
  int need, serve, s0, s1;
  vector<pair<int, int>> op;

  List (vector<int> v) {
    // for (auto i : v) {
    //   cout << i << ' ';
    // }
    // cout << '\n';
    s0 = s1 = 0;
    int cur = -1;
    auto ib = v.begin(), ie = --v.end();
    while (ie - ib > 1) {
      if (a[*ib][0] == a[*next(ib)][1]) {
        int p = *ib, q = *next(ib);
        op.push_back({q, p});
        a[p][1] = a[q][1], a[q][1] = 0;
        ++ib;
        continue;
      }
      if (a[*ie][0] == a[*prev(ie)][1]) {
        int p = *ie, q = *prev(ie);
        op.push_back({q, p});
        a[p][1] = a[q][1], a[q][1] = 0;
        --ie;
        continue;
      }
      vector<int> t;
      auto ip = ib;
      while (a[*ip][1] != a[*next(ip)][1])
        t.push_back(*++ip);
      op.push_back({*ip, cur});
      op.push_back({*next(ip), cur});
      a[*ip][1] = a[*next(ip)][1] = 0;
      for (auto i = t.rbegin(); i != --t.rend(); ++i) {
        int p = *i, q = *next(i);
        op.push_back({q, p});
        a[p][1] = a[q][1], a[q][1] = 0;
      }
      int p = *next(ib), q = *ib;
      op.push_back({q, p});
      a[p][1] = a[q][0], a[q][0] = 0;
      cur = q;
      ib = next(ip);
    }
    int p = *ib, q = *ie, s = q;
    op.push_back({q, p});
    a[p][1] = a[q][0], a[q][0] = 0;
    if (cur == -1) {
      need = 0, serve = 1, s0 = s;
    }
    else {
      need = 1, serve = 2, s0 = cur, s1 = s;
    }
  }
}; 

struct Cycle {
  int need, serve, s0, s1;
  vector<pair<int, int>> op; 

  Cycle (vector<int> v) {
    // for (auto i : v) {
    //   cout << i << ' ';
    // }
    // cout << '\n';
    for (int i = 0; i < v.size(); ++i) {
      int p = v[i], q = v[(i + 1) % v.size()];
      if (a[p][1] == a[q][1]) {
        a[p][1] = a[q][1] = 0;
        vector<int> v2;
        for (int j = i + 1; j < v.size(); ++j) {
          v2.push_back(v[j]);
        }
        for (int j = 0; j <= i; ++j) {
          v2.push_back(v[j]);
        }
        List l(v2);
        need = serve = l.need + 1;
        op.push_back({p, -need});
        op.push_back({q, -need});
        // for (auto i : l.op) {
        //   op.push_back(i);
        // }
        Append(op, l.op);
        s0 = l.s0, s1 = l.s1;
        return;
      }
    }
    need = serve = 1;
    if (a[v[0]][0] != a[v[1]][1])
      reverse(v.begin(), v.end());
    op.push_back({v[0], -1});
    a[v[0]][1] = 0;
    for (int i = 0; i < v.size() - 1; ++i) {
      int p = v[i], q = v[i + 1];
      op.push_back({q, p});
      a[p][1] = a[q][1], a[q][1] = 0;
    }
    a[v.back()][0] = 0, op.push_back({v.back(), -1});
    s0 = v.back();
  }
}; 

int main () {
  // freopen("tmp.in", "r", stdin);
  // freopen("tmp.out", "w", stdout);
  cin.tie(0)->sync_with_stdio(0);
  cin >> n >> m;
  for (int i = 1; i <= m; ++i) {
    int &x = a[i][0], &y = a[i][1];
    cin >> x >> y;
    (!pa[x] ? pa[x] : pb[x]) = i;
    (!pa[y] ? pa[y] : pb[y]) = i;
  }
  vector<int> spare;
  for (int i = 1; i <= m; ++i) {
    if (!a[i][0] && !a[i][1])
      spare.push_back(i);
  }
  for (int i = 1; i <= n; ++i) {
    if (pa[i] != pb[i])
      Add_edge(pa[i], pb[i]);
  }
  vector<List> lv[2];
  vector<Cycle> cv[2];
  for (int i = 1; i <= m; ++i) {
    if (e[i].size() == 1 && !vis[i]) {
      cur.clear(), Dfs(i);
      List l = List(cur);
      lv[l.need].push_back(l);
    }
  }
  for (int i = 1; i <= m; ++i) {
    if (e[i].size() == 2 && !vis[i]) {
      cur.clear(), Dfs(i);
      Cycle c = Cycle(cur);
      cv[c.need - 1].push_back(c);
    }
  }
  // cout << "Spare " << '\n';
  // for (auto i : spare) {
  //   cout << i << ' ';
  // }
  // cout << '\n';
  // for (auto list : lv[0]) {
  //   cout << "List " << list.need << ' ' << list.serve << ' ' << list.s0 << ' ' << list.s1 << '\n';
  //   for (auto i : list.op) {
  //     cout << i.first << ' ' << i.second << '\n';
  //   }
  // }
  // for (auto list : lv[1]) {
  //   cout << "List " << list.need << ' ' << list.serve << ' ' << list.s0 << ' ' << list.s1 << '\n';
  //   for (auto i : list.op) {
  //     cout << i.first << ' ' << i.second << '\n';
  //   }
  // }
  // for (auto cycle : cv[0]) {
  //   cout << "Cycle " << cycle.need << ' ' << cycle.serve << ' ' << cycle.s0 << ' ' << cycle.s1 << '\n';
  //   for (auto i : cycle.op) {
  //     cout << i.first << ' ' << i.second << '\n';
  //   }
  // }
  // for (auto cycle : cv[1]) {
  //   cout << "Cycle " << cycle.need << ' ' << cycle.serve << ' ' << cycle.s0 << ' ' << cycle.s1 << '\n';
  //   for (auto i : cycle.op) {
  //     cout << i.first << ' ' << i.second << '\n';
  //   }
  // }
  vector<pair<int, int>> ans;
  for (auto l : lv[0]) {
    spare.push_back(l.s0);
    Append(ans, l.op);
  }
  for (auto l : lv[1]) {
    if (spare.empty()) {
      cout << -1 << '\n';
      return 0;
    }
    int serv = spare.back();
    spare.pop_back();
    for (auto &i : l.op) {
      if (i.second == -1)
        i.second = serv;
    }
    Append(ans, l.op);
    spare.push_back(l.s0), spare.push_back(l.s1);
  }
  for (auto c : cv[0]) {
    if (spare.empty()) {
      cout << -1 << '\n';
      return 0;
    }
    int serv = spare.back();
    spare.pop_back();
    for (auto &i : c.op) {
      if (i.second == -1)
        i.second = serv;
    }
    Append(ans, c.op);
    spare.push_back(c.s0);
  }
  for (auto c : cv[1]) {
    if (spare.size() < 2) {
      cout << -1 << '\n';
      return 0;
    }
    int s[2];
    s[0] = spare.back();
    spare.pop_back();
    s[1] = spare.back();
    spare.pop_back();
    for (auto &i : c.op) {
      if (i.second < 0)
        i.second = s[(-i.second) - 1];
    }
    Append(ans, c.op);
    spare.push_back(c.s0), spare.push_back(c.s1);
  }
  cout << ans.size() << '\n';
  for (auto i : ans) {
    cout << i.first << ' ' << i.second << '\n';
  }
  return 0;
}