简单有效的kmp算法

以前看过kmp算法，当时接触后总感觉好深奥啊，抱着数据结构的数啃了一中午，最终才大致看懂，后来提起kmp也只剩下“奥，它是做模式匹配的”这点干货。最近有空，翻出来算法导论看看，原来就是这么简单（先不说程序实现，思想很简单）。

模式匹配的经典应用：从一个字符串中找到模式字串的位置。如“abcdef”中“cde”出现在原串第三个位置。从基础看起

朴素的模式匹配算法

A：abcdefg  B：cde

首先B从A的第一位开始比较，B++==A++，如果全部成立，返回即可；如果不成立，跳出，从A的第二位开始比较，以此类推。

/*
 *侯凯,2014-9-16
 *功能：模式匹配
 */
#include<iostream>
#include <string>
using namespace std;

int index(char *a,char *b)
{
    int tarindex = ;
    while(a[tarindex]!='\0')
    {
        int tarlen = tarindex;
        int patlen;
        for(patlen=;b[patlen]!='\0';patlen++)
        {
            if(a[tarlen++]!=b[patlen])
            {
                break;
            }
        }
        if(b[patlen]=='\0')
        {
            return tarindex;
        }
        tarindex++;
    }
    return -;
}
int main()
{
    char *a = "abcdef";
    char *b = "cdf";
    cout<<index(a,b)<<endl;
      system("Pause");
}

思路朴实无华，十分有效，但是时间复杂度是O(mn)，m、n分别是字符串和模式串的长度。模式匹配是一个常见的应用问题，用的广了，就有人想法去优化了。Rabin-Karp算法、有限自动机等等，前仆后继，最终出现了KMP(Knuth-Morris-Pratt)算法。

kmp算法

优化的地方：如果我们知道模式中a和后面的是不相等的，那么第一次比较后，发现后面的的4个字符均对应相等，可见a下次匹配的位置可以直接定位到f了。说明主串对应位置i的回溯是不必要的。这是kmp最基本最关键的思想和目标。

再比如：

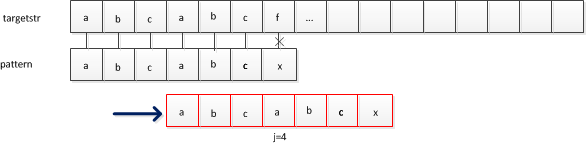
由于abc 与后面的abc相等，可以直接得到红色的部分。而且根据前一次比较的结果，abc就不需要比较了，现在只需从f-a处开始比较即可。说明主串对应位置i的回溯是不必要的。要变化的是模式串中j的位置（j不一定是从1开始的，比如第二个例子）

j的变化取决于模式串的前后缀的相似度，例2中abc和abc（靠近x的），前缀为abc，j=4开始执行。

j是前一次执行的模式子串（前几个，上例为6）中前缀的个数+1；它与模式字串中从前向后的前缀和从后向前的后缀的相同子串是有关系的，因为下次这部分相同的前缀就会移动到这部分后缀的位置，因为如果移动到后缀的前面位置，看图：

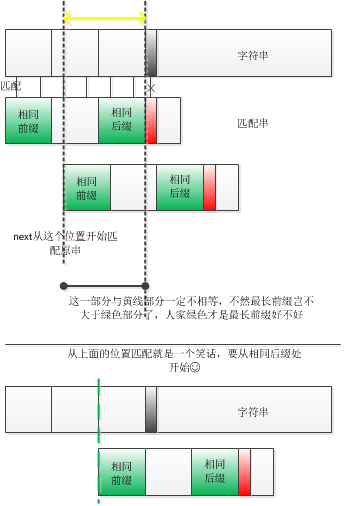
所以如果这次是j，下次的位置应该就是j前面的子串的最大前缀的长度+1,用这个新的位置再和原字符串的i位置进行比较就很幸福了。

这次是j，下次到底是多少呢，这就涉及到怎么计算的问题了？其实只看模式串我们就可以构建出这个j->x的关系，关系称为前缀函数，结果存储在数组中，称为前缀数组。

伪代码：

compiter-prefix-function(P)
    m<-length[p]
    pi[]<-
    k<-
    for q<- to m
        do while k> and P[k+]!=P[q]
                    do k<-pi[k] //前缀的前缀...
           if P[k+]==P[q]
                    then k<-k+
           pi[q]<-k
    return pi

使用前缀数组可很快地实现模式匹配，程序匹配字符串中模式出现的所有位置。

kmp-matcher(T, P)
    n<-length[T]
    m<-length[P]
    pi<-compiter-prefix-function(P)
    q<-
    for i<- to n
        do while q> and P[q+]!=T[i]
            do q<-pi[q] //前缀的前缀...
        if P[q+]==T[i]
            then q<-q+
        if q==m
            then print “Pattern occurs with shift”i-m
                    q<-pi[q]

这两段代码思想完全相同,如果和前缀不同就比较前缀的前缀…，比较巧妙。如果kmp有难理解的地方，估计就是这段伪码的了。

KMP算法的时间复杂度为O(n+m)。

这里需要强调一下，KMP算法的仅当模式与主串之间存在很多部分匹配情况下才能体现它的优势，部分匹配时KMP的i不需要回溯，否则和朴素模式匹配没有什么差别。