Not All Samples Are Created Equal: Deep Learning with Importance Sampling

概
主要内容
"代码"

Katharopoulos A, Fleuret F. Not All Samples Are Created Equal: Deep Learning with Importance Sampling[J]. arXiv: Learning, 2018.

@article{katharopoulos2018not,

title={Not All Samples Are Created Equal: Deep Learning with Importance Sampling},

author={Katharopoulos, Angelos and Fleuret, F},

journal={arXiv: Learning},

year={2018}}

概

本文提出一种删选合适样本的方法, 这种方法基于收敛速度的一个上界, 而并非完全基于gradient norm的方法, 使得计算比较简单, 容易实现.

主要内容

设\((x_i,y_i)\)为输入输出对, \(\Psi(\cdot;\theta)\)代表网络, \(\mathcal{L}(\cdot, \cdot)\)为损失函数, 目标为

\[\tag{1}
\theta^* = \arg \min_{\theta} \frac{1}{N} \sum_{i=1}^N\mathcal{L}(\Psi(x_i;\theta),y_i),
\]

其中\(N\)是总的样本个数.

假设在第\(t\)个epoch的时候, 样本(被选中)的概率分布为\(p_1^t,\ldots,p_N^t\), 以及梯度权重为\(w_1^t, \ldots, w_N^t\), 那么\(P(I_t=i)=p_i^t\)且

\[\tag{2}
\theta_{t+1}=\theta_t-\eta w_{I_t}\nabla_{\theta_t} \mathcal{L}(\Psi(x_{I_t};\theta_t),y_{I_t}),
\]

在一般SGD训练中\(p_i=1/N,w_i=1\).

定义\(S\)为SGD的收敛速度为:

\[\tag{3}
S :=-\mathbb{E}_{P_t}[\|\theta_{t+1}-\theta^*\|_2^2-\|\theta_t-\theta^*\|_2^2],
\]

如果我们令\(w_i=\frac{1}{Np_i}\) 则

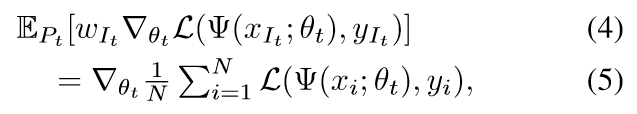
定义\(G_i=w_i\nabla_{\theta_t} \mathcal{L}(\Psi(x_{i};\theta_t),y_{i})\)

我们自然希望\(S\)能够越大越好, 此时即负项越小越好.

定义\(\hat{G}_i \ge \|\nabla_{\theta_t} \mathcal{L}(\Psi(x_{i};\theta_t),y_{i})\|_2\), 既然

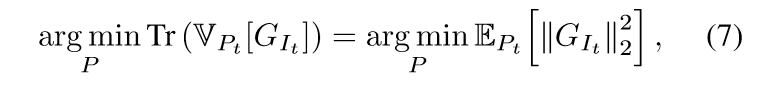
(7)式我有点困惑，我觉得(7)式右端和最小化(6)式的负项(\(\mathrm{Tr}(\mathbb{V}_{P_t}[G_{I_t}])+\|\mathbb{E}_{P_t}[G_{I_t}]\|_2^2\))是等价的.

于是有

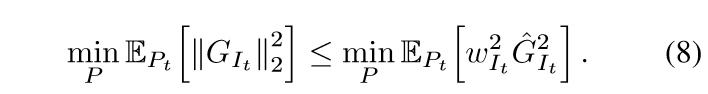
最小化右端(通过拉格朗日乘子法)可得\(p_i \propto \hat{G}_i\), 所以现在我们只要找到一个\(\hat{G}_i\)即可.

这个部分需要引入神经网络的反向梯度的公式, 之前有讲过，只是论文的符号不同, 这里不多赘诉了.

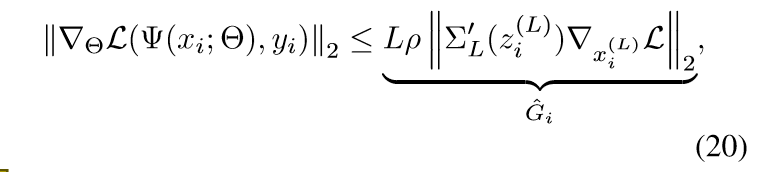
注意\(\rho\)的计算是比较复杂的, 但是\(p_i \propto \hat{G}_i\), 所以我们只需要计算\(\|\cdot\|\)部分, 设此分布为\(g\).

另外, 在最开始的时候, 神经网络没有得到很好的训练, 权重大小相差无几, 这个时候是近似正态分布的, 所以作者考虑设计一个指标，来判断是否需要根据样本分布\(g\)来挑选样本. 作者首先衡量

显然当这部分足够大的时候我们可以采用分布\(g\)而非正态分布\(u\), 但是这个指标不易判断, 作者进步除以\(\mathrm{Tr}(\mathbb{V}_u[G_i])\).

显然\(\tau\)越大越好, 我们自然可以人为设置一个\(\tau_{th}\). 算法如下

最后, 个人认为这个算法能减少计算量主要是因为样本少了, 少在一开始用正态分布抽取了一部分, 所以...

"代码"

主要是\(\hat{G}_i\)部分的计算, 因为涉及到中间变量的导数, 所以需要用到retain_grad().

"""

这里只是一个例子

"""

import torch

import torch.nn as nn

class Net(nn.Module):

    def __init__(self):

        super(Net, self).__init__()

        self.dense = nn.Sequential(

            nn.Linear(10, 256),

            nn.ReLU(),

            nn.Linear(256, 10),

        )

        self.final = nn.ReLU()

    def forward(self, x):

        z = self.dense(x)

        z.retain_grad()

        out = self.final(z)

        return out, z

if __name__ == "__main__":

    net = Net()

    criterion = nn.MSELoss()

    x = torch.rand((2, 10))

    y = torch.rand((2, 10))

    out, z = net(x)

    loss = criterion(out, y)

    loss.backward()

    print(z.grad) #这便是我们所需要的