SVM引入拉格朗日乘子[转载]

转自：https://zhidao.baidu.com/question/494249074914968332.html

SVM使用拉格朗日乘子法更为高效地求解了优化问题。

SVM将寻找具有最大几何间隔划分超平面的任务转化成一个凸优化问题，如下所示：

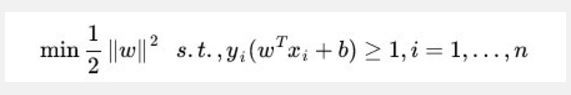
我们当然可以直接使用现成工具求解，但还有更为高效的方法，那就是使用拉格朗日乘子法将原问题转化为对偶问题求解。

具体做法是：

（1）将约束融入目标函数中，得到拉格朗日函数；

（2）然后对模型参数w和b求偏导，并令之为零；

（3）得到w后，将其带入拉格朗日函数中，消去模型参数w和b；

（4）这样就得到了原问题的对偶问题，对偶问题和原问题等价，同时对偶问题也是一个凸优化问题，使用SMO算法求解拉格朗日乘子；

（5）得到拉格朗日乘子后，进一步可以得到模型参数w和b，也就得到了我们想要的划分超平面。